Переходные процессы в линейных электрических цепях
После изучения данного раздела студенты должны:
Знать законы изменения токов и напряжений в простейших электрических цепях при переходном процессе решение уравнений электрического состояния цепи при переходном процессе;
Понимать причины возникновения переходных процессов в электрических цепях; законы коммутации; характер изменения токов и напряжений в электрических цепях при переходных процессах; смысл и значение постоянной времени;
Уметь составлять уравнения электрического состояния линейных электрических цепей при переходных процессах; определять постоянную времени простейших электрических цепей; определять закон изменения токов и напряжений в простейших линейных электрических цепях при переходных процессах.
Переходный (неустановившийся) процесс возникает в электрической цепи как в результате изменения параметров цепи, так и при негармоническом изменении величины приложенного напряжения.
Изучая переходные процессы, мы определяем закономерности изменения тока и напряжения в элементах электрических цепей в функции временя при переходе от одного установившегося состояния к другому. Переход от одного установившегося состояния к другому сопровождается изменением энергии магнитного поля в индуктивности и энергии электрического поля в емкости . Эти энергии не могут изменяться скачком, так как мощность, равная производной энергии по времени , должна в этом случае достигнуть бесконечно большого значения, что практически невозможно. Следовательно, если не могут скачком изменяться энергии , и , то не могут изменяться скачком ток i в индуктивности и напряжение u на емкости , что в обусловливает законы коммутации.
Для последовательной цели, содержащей 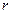 ,
, 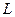 , и
, и 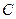 , уравнение, составленное по второму закону Кирхгофа, для мгновенных значений имеет следующий вид:
, уравнение, составленное по второму закону Кирхгофа, для мгновенных значений имеет следующий вид:
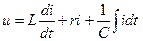 (9)
(9)
Это уравнение справедливо для любого момента времени, следовательно, оно справедливо как для установившегося состояния так и для переходного процесса. Уравнение (9) является неоднородным и его решение можно представить как сумму частного решения данного уравнения и общего решения однородного уравнения, которое получается из основного уравнения путем замены напряжения и нулем.
Решением уравнения для переходного процесса являются показательные и тригонометрические функции, играющие главенствующую роль при исследовании переходных процессов. Представим себе, что уравнение (9) рассматривается для установившегося состояния. Назовем ток установившегося состояния «установившимся» током и будем обозначать через 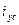 . тогда уравнение (9) примет вид
. тогда уравнение (9) примет вид
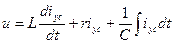 (10)
(10)
Вычитая уравнение (10) из уравнения (9), получаем
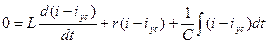 (11)
(11)
В полученном уравнении разность токов 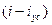 является ничем иным, как некоторым током, который существует в электрической цепи только во время переходного процесса; напряжение и равно нулю и ток
является ничем иным, как некоторым током, который существует в электрической цепи только во время переходного процесса; напряжение и равно нулю и ток 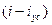 существует как бы независимо от приложенного к цепи внешнего напряжений. В силу сказанного этот ток называют «свободным» и обозначают через
существует как бы независимо от приложенного к цепи внешнего напряжений. В силу сказанного этот ток называют «свободным» и обозначают через 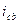 :
:
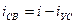 .
.
Откуда
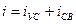 . (11а)
. (11а)
Как показывает, выражение (11а), ток переходного процесса может быть получен как сумма двух токов, одним из которых является, ток установившегося состояния 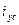 , определяемый как частное решение дифференциального уравнения (9), а вторым — ток, который определяется как общее решение соответствующего однородного уравнения.
, определяемый как частное решение дифференциального уравнения (9), а вторым — ток, который определяется как общее решение соответствующего однородного уравнения.
Заменяя 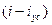 в уравнении (11) на
в уравнении (11) на 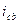 , получаем однородное дифференциальное уравнение для Определения свободного тока:
, получаем однородное дифференциальное уравнение для Определения свободного тока:
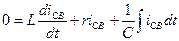 . (11б)
. (11б)
Таким образом, для исследования переходного процесса в последовательной цепи составляется дифференциальное уравнение описывающее переходный процесс (9), уравнение, определяющее собой ток установившегося состояния (10), и однородное дифференциальное уравнение для свободного тока (116).
Для решения однородного дифференциального уравнения свободного тока составляется характеристическое уравнение, для чего однородное дифференциальное уравнение свободного тока записывается в алгебраической форме путем замены производной 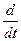 через оператор
через оператор  , а интеграла
, а интеграла 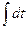 через
через 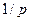 .
.
Произведя указанные операции над уравнением (116), получаем
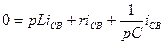 .
.
Вынося за скобку 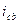 , получаем
, получаем
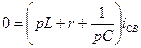 .
.
Так как здесь 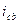 не равен нулю, то
не равен нулю, то
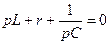 .
.
Откуда получаем искомое характеристическое уравнение
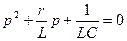 .
.
Показатель степени 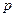 определяет порядок дифференциального уравнения свободного тока. Как видно в последовательной цепи, содержащей
определяет порядок дифференциального уравнения свободного тока. Как видно в последовательной цепи, содержащей 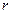 ,
, 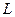 и
и 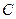 , мы имеем дифференциальное уравнение второго порядка.
, мы имеем дифференциальное уравнение второго порядка.
Определяем корни характеристического уравнения:
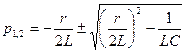 .
.
В зависимости от значения корней характеристического уравнения (соотношения между параметрами цепи 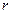 ,
, 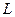 и
и 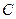 ) будут получены частные решения однородного дифференциального уравнения свободного тока:
) будут получены частные решения однородного дифференциального уравнения свободного тока:
1.Если 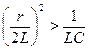 , решение для свободного тока имеет вид
, решение для свободного тока имеет вид
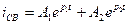 .
.
2.Если 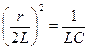 , решение для свободного тока имеет вид
, решение для свободного тока имеет вид
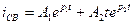
3.Если 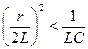 , решение для свободного тока имеет вид
, решение для свободного тока имеет вид
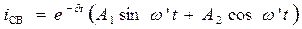 ;
;
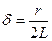 ;
; 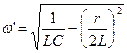 ,
,
где 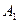 и
и 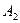 — постоянные интегрирования;
— постоянные интегрирования; 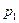 и
и 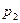 — корни характеристического уравнения.
— корни характеристического уравнения.
Корни характеристического уравнения в последнем случае соответственно равны: 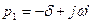 ,
, 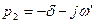
Рассмотрим несколько задач.
Задача.1. Определить ток переходного процесса при подключении катушки (последовательная цепь r и L) как па постоянное, так и на синусоидальное напряжения.
Дано: 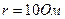 ,
, 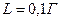 , для постоянного напряжения
, для постоянного напряжения 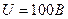 , для синусоидального напряжения
, для синусоидального напряжения 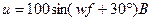 ,
, 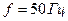 .
.
1. Постоянное напряжение. Определяем ток установившегося положения:
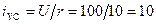 А.
А.
Уравнение свободного тока
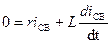 .
.
Его характеристическое уравнение
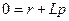 ,
,
откуда корень характеристического уравнения
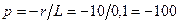 .
.
Свободный ток
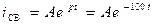 А.
А.
Ток переходного процесса
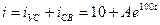 А.
А.
Определяем постоянную интегрирования 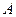 . Полагая
. Полагая 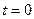 и учитывая, что ток в индуктивности скачком возникнуть не может (цепь до начала переходное процесса была разомкнута
и учитывая, что ток в индуктивности скачком возникнуть не может (цепь до начала переходное процесса была разомкнута 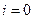 ), получим
), получим
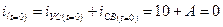 .
.
откуда A = —10.
Таким образом, ток переходного процесса будет равен
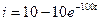 А.
А.
2. Синусоидальное напряжение. Определяем установившийся ток:
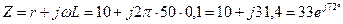 Ом;
Ом;
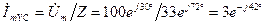 Ом;
Ом;
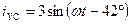 А.
А.
Так как свободный ток не зависит от напряжения, то воспользуемся его выражением, полученным в предыдущей задаче. Тогда ток переходного процесса
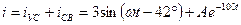 А.
А.
Определяем постоянную интегрирования 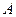 :
:
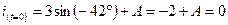 ,
,
откуда 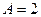 .
.
Таким образом, ток переходного процесса будет равен
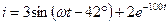 А.
А.
Задача 2. Определить ток переходного процесса в последовательной цепи с активным сопротивлением и емкостью при подключении ее как к постоянному, так и к синусоидальному напряжениям.
Дано: 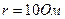 ,
, 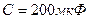 , для постоянного напряжения
, для постоянного напряжения 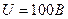 , для синусоидального напряжения
, для синусоидального напряжения 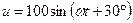 В,
В, 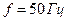 .
.
1. Постоянное напряжение. Установившийся ток в цепи с емкостью, подключенной к постоянному напряжению, равен нулю, так как конденсатор, зарядившись до величины питающего напряжения, размыкает цепь.
Следовательно, ток переходного процесса определяется только
свободным током. Уравнение свободного тока
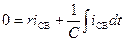 .
.
Дифференцируя уравнение свободного тока, получаем
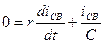 ,
,
тогда характеристическое уравнение
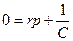 ,
,
откуда корень характеристического уравнения
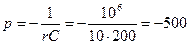 .
.
Ток переходного процесса
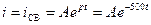 А.
А.
Определяем постоянную интегрирования А. Полагая 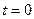 и учитывая, что напряжение на емкости скачком возникнуть не может (конденсатор до начала переходного процесса не был заряжен,
и учитывая, что напряжение на емкости скачком возникнуть не может (конденсатор до начала переходного процесса не был заряжен, 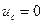 ), получаем
), получаем
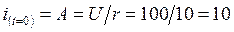 А.
А.
Таким образом, ток переходного процесса будет равен
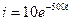 А.
А.
1. Синусоидальное напряжение. Определяем установившимся ток :
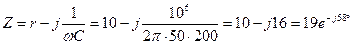 Ом;
Ом;
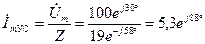 А;
А;
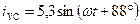 А.
А.
Воспользуемся выражением для свободного тока из предыдущей задачи. Тогда ток переходного процесса
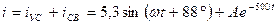 А.
А.
Определяем постоянную интегрирования 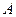 :
:
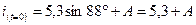 ,
,
откуда 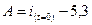 .
.
Найдем ток 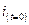 в момент включения:
в момент включения:
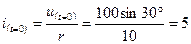 А,
А,
следовательно, 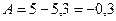 .
.
Таким образом, ток .переходного процесса будет равен
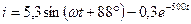 А.
А.
Задача 3. Определить емкость 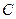 конденсатора в схеме с последовательным соединением резистора и конденсатора, включенной на постоянное напряжение
конденсатора в схеме с последовательным соединением резистора и конденсатора, включенной на постоянное напряжение 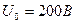 , из условия, что через время
, из условия, что через время 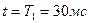 после включения напряжение на конденсаторе при заряде его через резистор с сопротивлением
после включения напряжение на конденсаторе при заряде его через резистор с сопротивлением 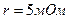 достигнет значения
достигнет значения 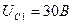 . Найти значение тока
. Найти значение тока 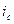 в момент
в момент 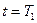 .
.
Решение. Выражение для напряжения, на конденсаторе во время переходного процесса в рассматриваемой цепи имеет вид 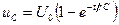 .Из этого выражения определим значение емкости конденсатора
.Из этого выражения определим значение емкости конденсатора 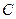 . При
. При 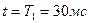 ,
, 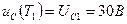 следовательно,
следовательно, 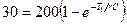 ,откуда
,откуда 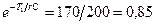 .Отсюда
.Отсюда 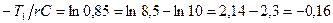 , т.е.
, т.е. 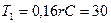 мс.
мс.
Окончательно
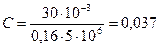 мкФ.
мкФ.
Выражение для тока в цепи запишем в виде
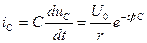 .
.
Подставляя в это выражение значения 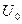 ,
, 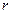 ,
, 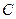 и
и 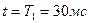 , найдем
, найдем
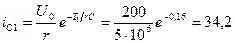 мкА.
мкА.
 Периодические несинусоидальные токи в электрических цепях
Периодические несинусоидальные токи в электрических цепях
После изучения данного раздела студенты должны:
1)знать значение терминов: электрический фильтр, амплитудно-частотный и фазочастотный спектры, коэффициент пульсаций, коэффициент искажения формы кривой; назначение сглаживающего, полосового, заградительного избирательного фильтров;
2)понимать причины возникновения несинусоидальных токов; принцип работы дифференцирующих и интегрирующих цепей; влияние формы кривой тока и напряжения на показания приборов различных систем;
3)уметь анализировать электрическое состояние линейной цепи несинусоидального тока методом суперпозиции, работу простейших фильтров.
При изучении настоящего раздела необходимо усвоить, что источников с абсолютно постоянной или синусоидальной э.д.с. не существует. Различные источники энергии в силу ряда причин создают пульсирующие, медленно меняющиеся или незначительно отличающиеся от синусоидальной формы напряжения.
Причинами появления несинусоидальных токов являются:
1)несовершенство источников постоянной и синусоидальной э.д.с.;
2)подключение к линейной цепи генераторов, создающих специальную форму напряжения;
3)наличие различного рода нелинейных элементов в электрической цепи.
При расчете цепей, находящихся под воздействием периодических несинусоидальных Величин, необходимо знать способы их представления:
1)графики зависимости мгновенных значений, несинусоидальных токов и напряжений от времени;
2)аналитический способ разложения периодических функций в ряд Фурье, из которого для практических целей берут ограниченное число первых членов ряда. В разложении в ряд Фурье в общем случае представлены постоянная составляющая, основная (первая) гармоническая составляющая, имеющая период, равный периоду данного несинусоидального воздействия, высшие гармонические составляющие и их начальные фазы. Основную и высшие гармонические составляющие обычно называют просто гармониками Амплитуды и начальные фазы гармоник определяют спектральный состав несинусоидальной кривой, который может быть представлен в виде диаграмм амплитудно-частотного и фазо-частотного спектров.
При анализе электрических цепей с несинусоидальными напряжениями и токами частот имеют дело с действующими значениями этих-величин:
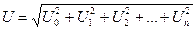 ;
;
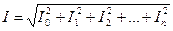 .
.
Таким образом, действующее значение несинусоидального напряжения или тока равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений всех гармоник несинусоидального напряжения или тока.
Действующее значение каждой гармоники
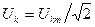 .
.
Среднее значение мощности при несинусоидальных напряжениях и токе равно сумме средних значений мощностей от постоянных составляющих и каждой гармоники тока и напряжения:
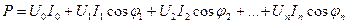 .
.
Форму периодических несинусоидальных кривых принято характеризовать некоторыми коэффициентами: амплитуды Ка, формы КФ, искажения Ки и др. Разложение в ряд Фурье позволяет заменить на основании принципа суперпозиции реальный источник несинусоидального напряжения совокупностью последовательно включенных
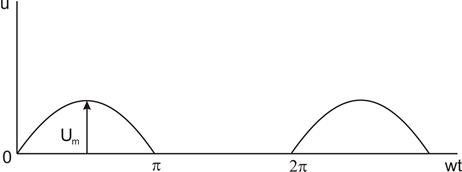
Рис. 23
источников. Таким образом, мгновенные значения искомых токов и напряжений определяют путем суммирования найденных и результат те расчета постоянных и гармонических составляющих тока или напряжения. При расчете цепей следует учитывать, что сопротивления емкостного и индуктивною элементов зависят от частоты: сопротивление индуктивного элемента возрастает с увеличением номера к гармоники, т.е. 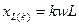 , а сопротивление емкостного элемента уменьшается с увеличением порядкового номера гармоники, т. е.
, а сопротивление емкостного элемента уменьшается с увеличением порядкового номера гармоники, т. е. 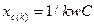 . В тех случаях, когда это требуется по условиям работы электрических цепей для изменения формы кривой тока или напряжения, применяются специальные устройства, содержащие индуктивные катушки и конденсаторы. Эти устройства называются электрическими фильтрами.
. В тех случаях, когда это требуется по условиям работы электрических цепей для изменения формы кривой тока или напряжения, применяются специальные устройства, содержащие индуктивные катушки и конденсаторы. Эти устройства называются электрическими фильтрами.
Задача 1. Для кривой напряжения однополупериодного выпрямления 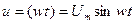 (рис. 23). Найти действующее значение напряжения путем непосредственного интегрирования. Сравнить найденный результат с расчетом по гармоникам ряда Фурье, учитывая только: а) первый член ряда, б) первые три члена ряда. Оценить погрешность
(рис. 23). Найти действующее значение напряжения путем непосредственного интегрирования. Сравнить найденный результат с расчетом по гармоникам ряда Фурье, учитывая только: а) первый член ряда, б) первые три члена ряда. Оценить погрешность 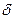 в процентах. Определить коэффициенты
в процентах. Определить коэффициенты 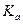 ,
, 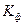 ,
, 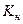 .
.
Разложение в ряд Фурье:
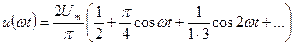 .
.
Решение. Находим действующее и среднее значения напряжения непосредственным интегрированием:
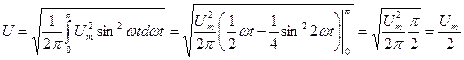 ;
;
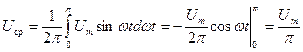 .
.
Учитывая только первый член разложения в ряд Фурье, оценим погрешность 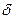 :
:
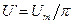 ;
;
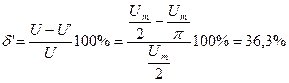 .
.
С учетом первых трех членов разложения получим
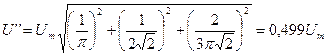 ;
;
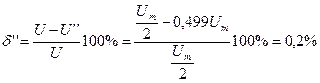 .
.
Получаем погрешность, вполне допустимую при инженерных расчетах. Таким образом, остальными членами разложения в ряд Фурье можно пренебречь.
Определим коэффициенты, характеризующие форму кривой напряжения:
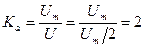 ;
; 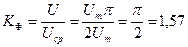 ;
;
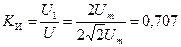 .
.
Задача 2. Определить индуктивности 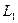 и
и 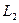 резонансного фильтра (рис. 24), являющегося бесконечно большим сопротивлением для тока первой гармоники и не представляющего сопротивления для тока седьмой гармоники. Дано;
резонансного фильтра (рис. 24), являющегося бесконечно большим сопротивлением для тока первой гармоники и не представляющего сопротивления для тока седьмой гармоники. Дано; 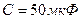 ,
, 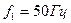 .
.
Решение. Чтобы исключить первую гармонику в нагрузке, необходимо выполнить условие резонанса токов: 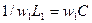 , отсюда
, отсюда
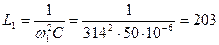 мГ.
мГ.
Чтобы выделить седьмую гармонику в нагрузке ZH , следует обеспечить условие резонанса напряжений для седьмой гармоники:
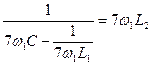 ,
,
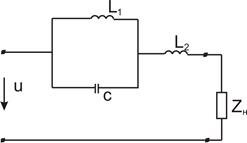
Рис. 24
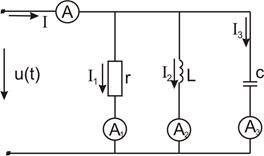
Рис. 25
Отсюда
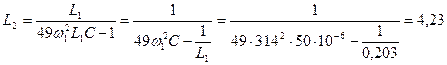 мГ.
мГ.
Задача 3. Найти показания приборов электромагнитной системы (рис. 25), записать выражения для мгновенных значений всех токов и определить их коэффициенты искажения. Дано: 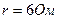 ,
, 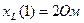 ,
, 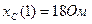 ,
, 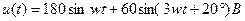 .
.
Решение. Находим токи в ветвях от первой гармоники:
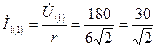 А;
А;
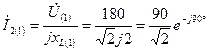 А;
А;
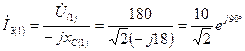 А;
А;
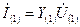 ,
,
где 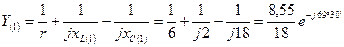 1/Ом;
1/Ом;
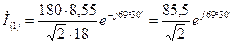 А.
А.
Определяем токи в ветвях от третьей гармоники:
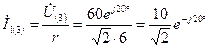 А;
А;
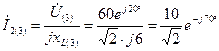 А;
А;
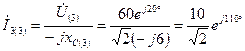 А.
А.
На третьей гармонике в параллельном контуре резонанс токов
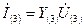 ,
,
где 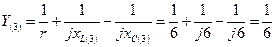 1/Ом;
1/Ом;
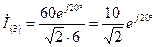 А.
А.
Показания приборов будут иметь следующие значения:
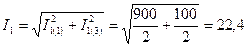 А;
А;
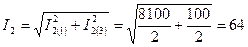 А;
А;
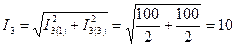 А;
А;
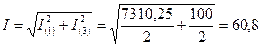 А.
А.
Мгновенные значения токов имеют вид:
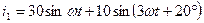 А;
А;
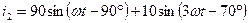 А;
А;
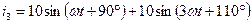 А;
А;
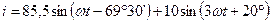 А.
А.
Коэффициенты искажения, токов:
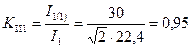 ;
;
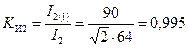 ;
;
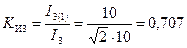 ;
;
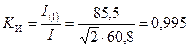 .
.
Наиболее искажена кривая тока на емкостном элементе.
Магнитные цепи
Дата добавления: 2015-12-10; просмотров: 1496;
