Электрические цепи переменного тока. В результате изучения данного раздела студенты должны:
Однофазные цепи
В результате изучения данного раздела студенты должны:
1)знать содержание терминов: резистор, сопротивление, индуктивная катушка, индуктивность, индуктивное сопротивление, конденсатор, емкость, емкостное сопротивление, фаза, начальная фаза, угол сдвига фазы, период, частота, угловая частота мгновенное, действующее и среднее значения гармонических величин, полное, активное, реактивное, комплексное сопротивления и проводимость; полная, активная, реактивная, комплексная мощность; характеристики и параметры элементов схем замещения цепей однофазного тока; условия достижения резонансов напряжении, и токов;
2)понимать особенности электромагнитных процессов в электрических цепях синусоидального тока, энергетические соотношения в цепях синусоидального тока, экономическое значение коэффициента мощности; особенности простейших электрических цепей с магнито-связанкыми элементами;
3)уметь составлять дифференциальные и комплексные уравнения состояния линейных цепей; представлять гармонически изменяющиеся величины тригонометрическими функциями, графиками, изображающими величинами и комплексными числами; строить векторные диаграммы неразветвленных цепей и цепей с параллельным соединением ветвей; определять опытным путем параметры схем замещения пассивных двухполюсников; с помощью электроизмерительных приборов измерять токи, напряжения и мощности в электрических цепях; строить потенциальные (топографические) диаграммы для неразветвленных цепей и цепей с параллельным соединением ветвей.
При изучении явлений резонанса в цепях переменного тока необходимо знать условия их возникновения, а также обратить внимание на практическое применение резонанса токов для искусственного повышения коэффициента мощности в промышленных электроустановках. В то же время возникновение резонанса напряжений в электрических устройствах может представлять опасность как для самих устройств, так и для обслуживающего персонала.
Изучая явления резонанса, необходимо усвоить следующее. При резонансе напряжение и ток на зажимах цепи всегда совпадает по фазе. Настройка же цепи на резонанс зависит от схемы соединений индуктивности и емкости. Для последовательной цепи условием резонанса является равенство индуктивного и емкостного сопротивлений: 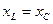 . Для цепи, содержащей параллельный контур, в одной из ветвей которого находится индуктивность, а в другой — емкость, условием резонанса является равенство реактивных проводимостей ветвей:
. Для цепи, содержащей параллельный контур, в одной из ветвей которого находится индуктивность, а в другой — емкость, условием резонанса является равенство реактивных проводимостей ветвей: 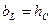 .
.
При расчете цепей синусоидального тока приходится совершать различные математические операции, которые удобно производить над действующими значениями токов и напряжений, рассматривая их как векторы. Величины векторов при этом равны действующим значениям тока и напряжения, а начальная фаза определяет положение вектора относительно положительной горизонтальной оси координат. При положительной (опережающей) начальной фазе вектор повернут на соответствующий угол против движения часовой стрелки, а при отрицательной (отстающей)— по направлению движения часовой стрелки. Совокупность векторов, изображающих синусоидальные э. д. с, напряжения и токи одной частоты, выходящих из общей точки, называют векторной диаграммой.
Для цепей синусоидального тока обычно строят потенциальную (топографическую) диаграмму, каждая точка которой соответствует определенной точке электрической цепи. Чтобы осуществить это соответствие точек диаграммы и цепи, построение потенциальной диаграммы ведут в той же последовательности, в какой обходят электрическую цепь. Обычно направление обхода выбирают противоположный принятому направлению тока в цепь. Для наглядности в некоторых случаях векторные и потенциальные диаграммы объединяют в одну. Необходимо обратить особое внимание на направление векторов на потенциальных диаграммах. Векторы напряжений направлены относительно точек потенциальной диаграммы противоположно положительным направлениям напряжений относительно соответствующих точек цепи. Ценность потенциальной диаграммы состоит в том что она позволяет определять напряжения между любыми точками цепи. Для этого следует соединить соответствующие точки потенциальной диаграммы отрезком прямой и придать этому отрезку соответствующее направление.
При помощи потенциальной диаграммы удобно производить сложение напряжений, возникающих на отдельных участках последовательной цепи (второй закон Кирхгофа), и сложение токов, протекающих в ветвях параллельной цепи (первый закон Кирхгофа).
При построении векторных диаграмм одни из векторов принимают за основной (опорный), располагая его обычно по положительному направлению горизонтальной оси. В этом случае начальная фаза тока или напряжения в зависимости от того, что данный вектор изображает, равна нулю. Для последовательной цепи за основной вектор принимают вектор тока, а для параллельной — вектор напряжения.
На рис. 12 показаны последовательная цепь (рис. 12,а) и ее векторная (рис. 12,б) и потенциальная (рис. 12, в) диаграммы. На рис. 13 в той. же последовательности, что- и на рис. 12, показана параллельная цепь и ее векторная и потенциальная диаграммы.
В том случае, когда сложение или вычитание вектора требуется производить не графически, а математически (например, при расчете электрической цепи), векторы раскладывают на две составляющие, одна из которых называется активной, а вторая — реактивной. Активной составляющей напряжения является та, которая совпадает по фазе 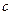 током, а реактивная — которая опережает ток или отстает от него по фазе на 90°. .Активной составляющей тока является та, которая совпадает по фазе с напряжением, а реактивной — которая опережает напряжение пли отстает от него по фазе на 90°. Зная сдвиг фаз между током и напряжением и величины векторов тока и напряжения, легко определить соответствующие составляющие этих векторов. Например, если нам задан синусоидально изменяющийся ток уравнением вида
током, а реактивная — которая опережает ток или отстает от него по фазе на 90°. .Активной составляющей тока является та, которая совпадает по фазе с напряжением, а реактивной — которая опережает напряжение пли отстает от него по фазе на 90°. Зная сдвиг фаз между током и напряжением и величины векторов тока и напряжения, легко определить соответствующие составляющие этих векторов. Например, если нам задан синусоидально изменяющийся ток уравнением вида 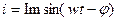 , то его активная и реактивная составляющие для действующего значения будут соответственно равны:
, то его активная и реактивная составляющие для действующего значения будут соответственно равны:
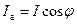 ,
, 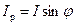
где 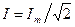
Аналогично для напряжении:
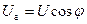 ;
; 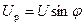 .
.
На диаграмме, изображенной на рис. 13,б, показаны активные
и реактивные составляющие токов.
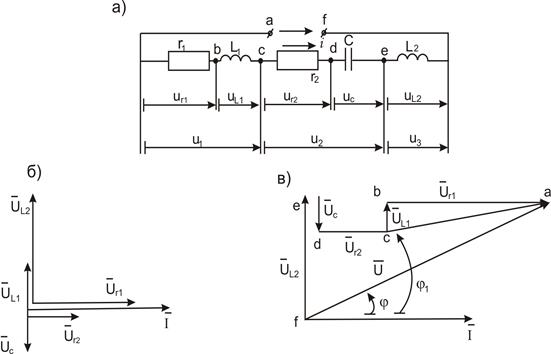
Рис. 12
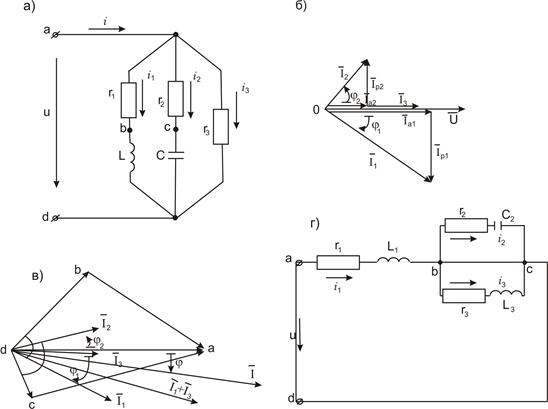
Рис. 13
В том случае, когда необходимо произвести сложение двух или более векторов, выражающих собой токи или напряжения, определяют их активные и реактивные составляющие и модуль результирующего вектора:
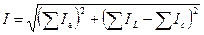 ;
; 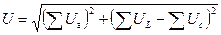 ,
,
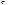
где индексы L и С указывают на характер реактивной составляющей (индуктивности или емкость). Начальная фаза результирующего вектора определяется через tg: 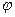
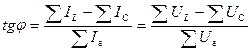
Для практических расчетов удобнее выражать векторы тока и напряжения, а также сопротивления и проводимости комплексными числами, в которых активные составляющие являются действительными величинами, а реактивные — мнимыми. Причем знак у мнимой величины зависит от характера активной составляющей. При расчете электрических цепей переменного тока с помощью комплексных чисел могут быть использованы методы расчета, применяемые для цепей постоянного тока. Уравнения Кирхгофа в этом случае записываются как составляющие геометрические суммы.
При выполнении расчетов по методу комплексных чисел следует иметь в виду, что вещественная и мнимая части комплексного сопротивления, комплексной проводимости и комплексной мощности всегда представляют собой соответственно активную и реактивную составляющие этих величин; что же касается комплексного напряжения и комплексного тока, что такое положение имеет место, лишь в частных случаях. Вещественная и мнимая части комплексного напряжения и комплексного тока определяются начальными фазами величии, иначе говоря, зависят от расположения соответствующих векторов относительно осей комплексной плоскости, тогда как их активная и реактивная составляющие определяются углом сдвига по фазе 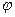 между этими двумя векторами,
между этими двумя векторами,
При анализе магнитосвязанных электрических цепей необходимо иметь в виду, что при составлении уравнения по второму закону Кирхгофа, при учете напряжения от взаимоиндукции сравнивается направление обхода рассматриваемой катушки и направление тока во влияющей на нес катушке относительно одноименных зажимов катушек. Если эти направления совпадают, то напряжение взаимоиндукции учитывается в уравнении со знаком плюс, в противном случае — с минусом.
Задача 1. Рассчитать электрическую цепь синусоидального тока со смешанным соединением приемников.
Для схемы, изображенной на рис. 13,г (на рис. 13,г ток 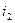 направлен по часовой стрелке, ток
направлен по часовой стрелке, ток 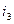 — против часовой стрелки), известно, что
— против часовой стрелки), известно, что
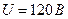 ,
, 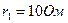 ,
, 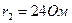 ,
, 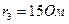 ,
,
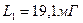 ,
, 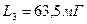 ,
, 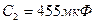 ,
, 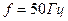 .
.
Определить токи 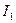 ,
, 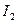 ,
, 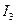 о ветвях цепи, напряжения па участках цепи
о ветвях цепи, напряжения па участках цепи 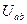 ,
, 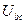 активную, реактивную и полную мощности и построить векторную диаграмму.
активную, реактивную и полную мощности и построить векторную диаграмму.
Решение. Выражаем сопротивления ветвей цепи в комплексной форме:
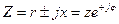
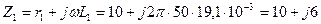 Ом.
Ом.
Переходя от алгебраической формы записи комплексного числа к показательной, получаем:
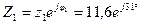 Ом,
Ом,
где 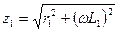 ;
; 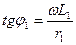
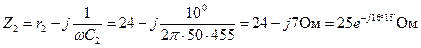 ;
;
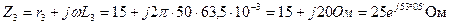
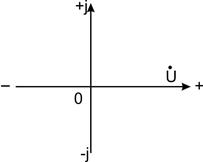
Рис. 14
Выражаем заданное напряжение 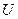 в комплексной форме. Если начальная фаза напряжения не задана, то ее можно принять равной нулю и располагать вектор напряжения совпадающим с положительным и направлением действительной оси. В этом случае мнимая составляющая комплексного числа будет отсутствовать (рис. 14):
в комплексной форме. Если начальная фаза напряжения не задана, то ее можно принять равной нулю и располагать вектор напряжения совпадающим с положительным и направлением действительной оси. В этом случае мнимая составляющая комплексного числа будет отсутствовать (рис. 14):
U =U = 120 В.
Полное комплексное сопротивление цепи
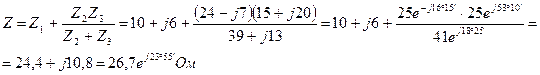
Определяем ток 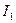 в неразветвленной части цепи:
в неразветвленной части цепи:
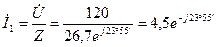 А.
А.
Токи 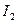 и
и 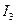 в параллельных ветвях могут быть выражены через ток в неразветвленной части цепи:
в параллельных ветвях могут быть выражены через ток в неразветвленной части цепи:
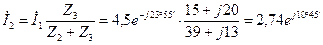 А;
А;
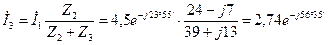 А.
А.
Токи 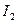 и
и 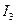 можно найти и по-другому:
можно найти и по-другому:
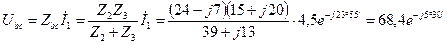 В;
В;
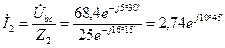 А;
А;
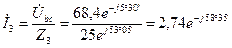 А.
А.
Найдем мощности всей цепи и отдельных ее ветвей:
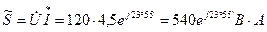
Для определения активной и реактивной мощностей полную мощность, выраженную комплексным числом в показательной форме, переводим в алгебраическую форму. Тогда действительная часть комплекса будет представлять собой активную мощность, а мнимая — реактивную:
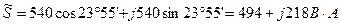 ,
,
откуда
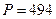 Вт;
Вт; 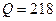 вар.
вар.
Активную и реактивную мощности можно найти и по-другому:
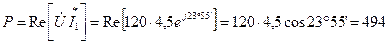 Вт;
Вт;
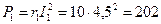 Вт;
Вт; 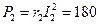 Вт;
Вт;
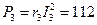 Вт.
Вт.
Проверка показывает, что 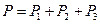 .
.
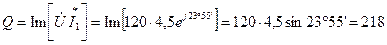 вар;
вар;
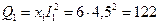 вар;
вар; 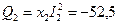 вар;
вар;
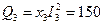 вар.
вар.
Учитывая, что 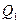 и
и 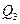 положительны (реактивная мощность индуктивных катушек), a
положительны (реактивная мощность индуктивных катушек), a 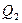 отрицательно (реактивная мощность конденсатора), получим
отрицательно (реактивная мощность конденсатора), получим 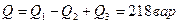 .
.
На рис.15 приведена векторная диаграмма токов и напряжений, построенная но расчетным данным. Порядок ее построения следующий: по результатам расчетов отложены векторы токов 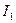
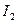 и
и 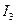 затем по направлению
затем по направлению 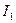 отложен вектор
отложен вектор 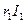 и перпендикулярно к нему в сторону опережения — вектор
и перпендикулярно к нему в сторону опережения — вектор 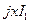 . Их сумма дает вектор
. Их сумма дает вектор 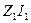 . Далее в фазе с
. Далее в фазе с 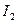 построен вектор
построен вектор 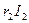 и перпендикулярно к нему в сторону отставания вектор
и перпендикулярно к нему в сторону отставания вектор 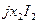 , а их сумма даст вектор напряжения на параллельном участке
, а их сумма даст вектор напряжения на параллельном участке 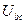 . Тот же вектор может быть получен, если в фазе с
. Тот же вектор может быть получен, если в фазе с 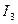 отложить.
отложить. 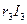 и к нему прибавить вектор
и к нему прибавить вектор 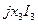 , опережающий
, опережающий 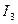 на 90°. Сумма векторов
на 90°. Сумма векторов 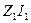 и
и 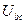 дает вектор приложенного напряжения
дает вектор приложенного напряжения 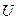 .
.
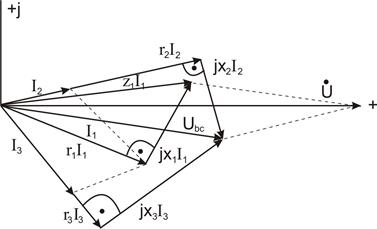
Рис. 15
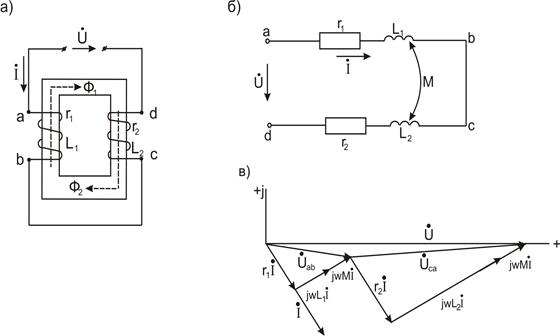
Рис.16
Задача2. Определить эквивалентное комплексное сопротивление цепи (рис.16,а), ток и напряжение между точками 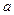 и
и 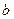 ,
, 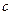 и
и 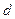 , если
, если 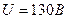 ,
, 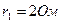 ,
, 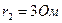 ,
, 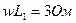 ,
, 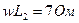 ,
, 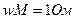 .
.
Решение. Из рис.16,а следует, что при заданном направлении тока в каждой катушке потоки самоиндукции и взаимной индукции одинаково направлены, Следовательно, катушки включены согласно. Заданная Цепь может быть представлена схемой замещения, показанной на рис.16,б. Составим для нее уравнение по второму закону Кирхгофа:
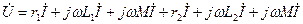 .
.
Эквивалентное комплексное сопротивление цепи
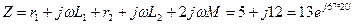 Ом.
Ом.
Искомый ток
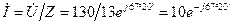 А.
А.
Комплексные напряжения между точками а и b, с и d равны:
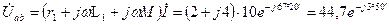 В;
В;
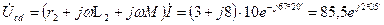 В.
В.
На рис, 16,в. представлена векторная диаграмма. По действительной оси отложен вектор напряжения, от него в сторону отставания на 67°20' направлен вектор тока, затем отложены векторы падения напряжения в каждой из катушек.
Трехфазные цепи
При изучении трехфазных цепей особое внимание необходимо обратить на преимущества, которые дает трехфазная система по сравнению с однофазной. Рассматривая схемы соединения обмоток генераторов, надо уяснить связь между фазными и линейными напряжениями в схеме соединения звездой, а также связь между фазными и линейными токами в схеме соединения треугольником.
Необходимо четко представить, что в трехфазной цепи могут быть два режима: симметричный и несимметричный. Расчет трехфазной, цепи в симметричном режиме сводится к расчету для одной фазы и производится аналогично расчету обычной цепи однофазного тока. Трехфазная цепь может, рассматриваться как разветвленная цепь с тремя источниками питания и для ее расчета применяются методы, используемые при расчете сложных электрических цепей. Например, если несимметричный приемник соединен звездой без нейтрального провода, то для расчета трехфазной цепи можно применить метод узлового напряжения в комплексной форме.
После изучения настоящего раздела студенты должны:
1)знать основные элементы трехфазных цепей, способы соединения фаз обмотки генератора а включения в трехфазную цепь приемников; способы изображения трехфазной симметричной системы
э. д. с;
2)понимать роль нейтрального провода; принципы построения потенциальных диаграмм; влияние рода и схемы включения нагрузки на величину тока в нейтральном проводе; схемы электроснабжения предприятий;
3)уметь анализировать различные режимы симметричных и не симметричных цепей; читать схемы соединения трехфазных и одно фазных приемников; предвидеть последствия коммутационных изменений в цепи на ее электрическое состояние.
Задача1. В трехфазную сеть с линейным напряжением 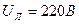 включен приемник, соединенный треугольником, сопротивление каждой фазы которого
включен приемник, соединенный треугольником, сопротивление каждой фазы которого 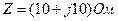 (рис. 17). Найти токи в каждой фазе нагрузки и ляпни и показания каждого ваттметра. Построить, векторную диаграмму. Найти те же величины в случае обрыва цепи в точке d.
(рис. 17). Найти токи в каждой фазе нагрузки и ляпни и показания каждого ваттметра. Построить, векторную диаграмму. Найти те же величины в случае обрыва цепи в точке d.
Решение. Расчет токов в трехфазных целях производится комплексным методом. Примем, что вектор линейного напряжения 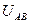 направлен по действительной оси, тогда
направлен по действительной оси, тогда
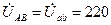 В;
В; 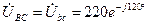 В;
В;
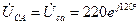 В.
В.
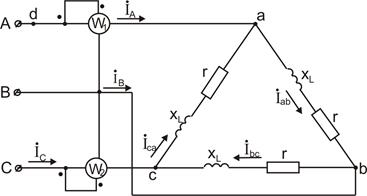
Рис. 17
Определяем фазные токи:
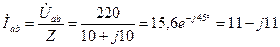 А;
А;
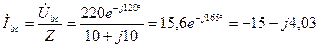 А;
А;
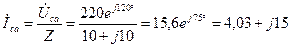 А.
А.
Находим линейные токи:
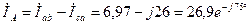 А;
А;
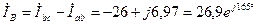 А;
А;
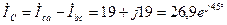 А.
А.
Определим, показания ваттметров:
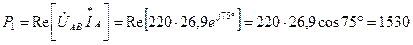 Вт;
Вт;
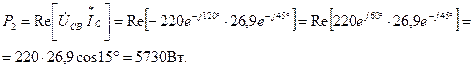
Активная мощность цепи (алгебраическая сумма показаний ваттметров) 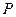 равна:
равна:
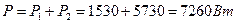 ,
,
или
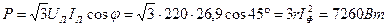 .
.
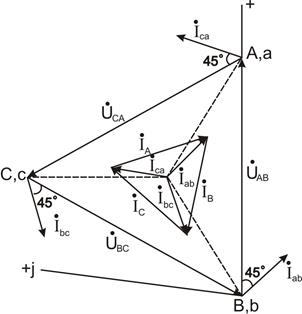
Рис. 18
На рис. 18 приводится векторная диаграмма напряжений и ков. При обрыве в точке 4; тока в фазах нагрузки будут:
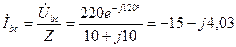
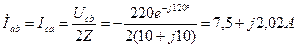
Вычислим линейные токи:
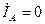 ;
; 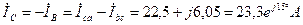 .
.
Находим показания ваттметров:
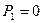 ;
; 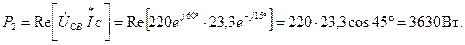
Задача 2. В четырехпроводную трехфазную сеть с линейным, напряжением 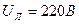 включен звездой приемник, активные и индуктивные сопротивления фаз которого соответственно равны:
включен звездой приемник, активные и индуктивные сопротивления фаз которого соответственно равны: 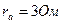 ,
, 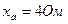 ,
, 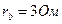 ,
, 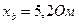 ,
, 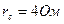 ,
, 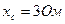 (рис.19). Определить токи в линейных и нейтральном проводах и построить векторную диаграмму.
(рис.19). Определить токи в линейных и нейтральном проводах и построить векторную диаграмму.
Решение. Считаем, что вектор фазного напряжения 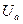 направлен по действительной оси, тогда
направлен по действительной оси, тогда
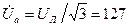 В,
В, 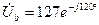 В,
В, 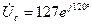 В.
В.
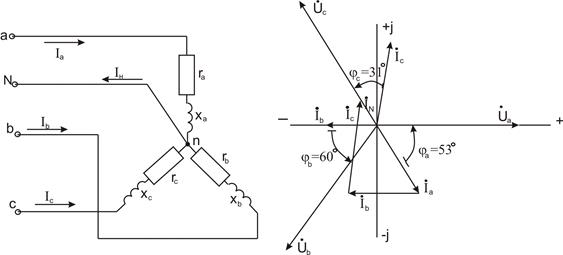
Рис. 19 Рис. 20
Находим линейные токи:
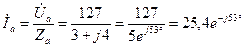 А;
А;
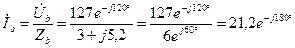 А;
А;
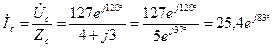 А.
А.
Ток в нейтральном проводе определяется как геометрическая сумма линейных токов:
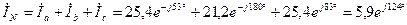 А.
А.
Векторная диаграмма показана на рис.20.
При несимметричной нагрузке для определения активной мощности находят мощность каждой фазы отдельно:
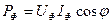 ,
,
а мощность всей трехфазной системы получают как сумму мощностей всех фаз или используют схему включения двух ваттметров.
Задача 3. В трехфазную сеть с линейным напряжением 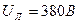 включен звездой приемник; активное, индуктивное иемкостное сопротивление фаз которого равны:
включен звездой приемник; активное, индуктивное иемкостное сопротивление фаз которого равны: 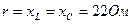 (рис. 21).
(рис. 21).
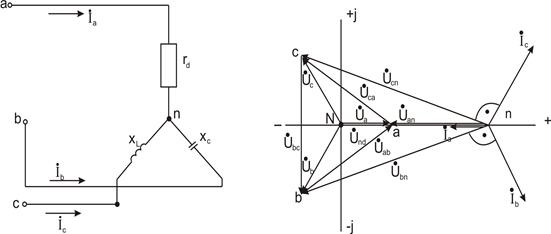
Рис. 21 Рис. 22
Решение. Расчет токов производит комплексным методом. Находим фазные напряжения:
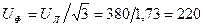 В;
В;
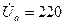 В;
В; 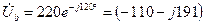 В;
В;
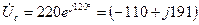 В.
В.
Определяем напряжение между нейтральными точками приемника и источника питания:
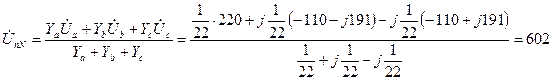 В.
В.
Определяем напряжения на зажимах фаз приемника:
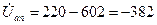 В;
В;
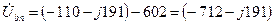 В;
В;
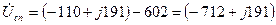 В.
В.
Определяем фазные (линейные) токи:
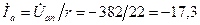 А;
А;
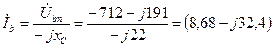 А;
А;
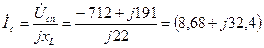 А.
А.
Векторная диаграмма изображена на рис. 22.
Для подсчета активной мощности в данной схеме можно воспользоваться уравнениями, записанными для схемы включения двух ваттметров. Из рассмотрения этой задачи следует, что напряжения на зажимах фаз приемника получаются неодинаковыми. Поэтому несимметричные приемники (Оптовые и др.) соединяют либо четырехпроводной звездой, либо треугольником.
Дата добавления: 2015-12-10; просмотров: 2496;
