Волны в стержнях (волны Порхгаммера)

Волны Порхгаммера – особый тип нормальных волн. Они возникают в стержнях, диаметр которых соизмерим с длиной волны. Волны Порхгаммера могут быть симметричными, антисимметричными, а также крутильными.

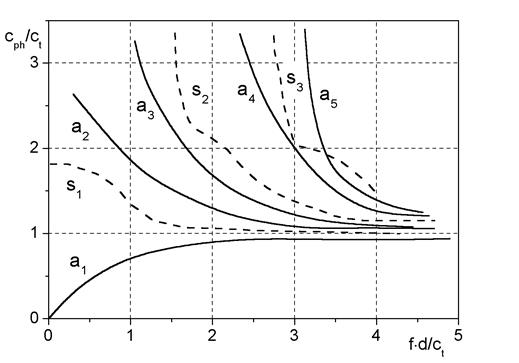
Рис. 2.8. Система дисперсионных кривых волн Порхгаммера

Особенности дисперсионных кривых:

1. Картина сложнее, чем для волн в пластинах:

а) число мод значительно увеличилось;

б) появились четные моды, обусловленные наличием крутильных волн, которые не имеют аналогов среди волн в пластинах;

в) критические значения, при которых фазовая скорость стремится к бесконечности, не означают целого числа полуволн, как в случае пластин, и вычисляются по более сложным формулам.

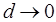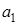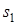2. Если диаметр стержня мал, т. е. , то существуют только моды и , что позволяет применять волны Порхгаммера для контроля прутков и проволоки. В этом случае фазовая и групповая скорости моды s₁ стремится к значению 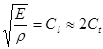. Для моды a₁ эти скорости близки к нулю. При этом выбирают такой тип колебаний, который легко возбуждается и обеспечивает хорошую выявляемость дефектов. Наиболее удобна мода 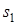, обладающая наименьшей дисперсией.

3. Без использования дисперсионных кривых условия возбуждения стержневых волн определяют по формуле:

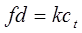, (2.9)

где 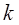– нормированный коэффициент (рекомендован ряд значений 0,83; 2,5; 3,8; 5,25…).

Выбирая меньшее значение коэффициента 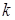, можно определить легко возбуждаемые низшие моды колебаний. Далее рассчитывают фазовую скорость:

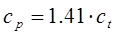(2.10)

Угол падения первичной волны определяют из закона Снеллиуса.

В заключение данного раздела следует отметить, что нормальные волны Порхгаммера, Лэмба и поверхностные волны Рэлея представляют собой результат интерференции объемных волн в ограниченных средах. Наличие границ раздела математически учитывается введением соответствующих граничных условий в волновом уравнении. Ограниченные среды, такие как пластины и стержни представляют собой своеобразные волноводы, в которых интерферирующие волны распространяются без рассеяния.

Основные характеристики различных типов волн в неограниченных и ограниченных средах приведены в табл. 4.

Таблица 4