Оценка достоверности различий показателей заболеваемости с помощью критерия t.
Критерий t – это критерий статистической значимости (достоверности) или доверительный коэффициент.
Критерий t рассчитывается по общей формуле:
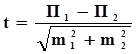(Знак разности не учитывается) где:
П1 и П2 – два любых относительных показателя, а именно:
· показатели инцидентности (заболеваемости) (I);
· показатели превалентности (PRM, PRP);
· экстенсивные показатели (Р);
·показатели человек-время (PtR));
m1 и m2 – стандартные ошибки сравниваемых показателей.
Как оценить величину критерия t ?
Значения критерия tвзаимосвязано с уровнем доверия (P) Это значит, что определённому значению tсоответствует только одно значение уровня (P). И наоборот, каждому значению уровня доверия (P) соответствует строго определённое значение критерия t. При этом чем больше значение критерия t, тем больше значение уровня доверия (Р) и, соответственно, меньше уровень ошибки (р). Так, при числе N больше 30:
· t= 0,675 соответствует значению P=0,50, и р =0,5
· t = 1,0 соответствует значению Р=0,6827; и р =0,3173
· t = 1,8 соответствует значению Р=0,9281; и р =0,0719
· t = 1,90 соответствует значению Р=0,9425; и р =0,0575
· t = 1,96 соответствует значению Р=0,95; и р =0,05
· t= 3,0 соответствует значению P=0,9973 и р=0,0027,
· Самое высокое значение Р=0,9997, и р=0,0003, (следовательно, ошибка составляет всего 0,03%), соответствует t=3,58. Дальнейшее увеличение значения t не изменяет значения Р или р.
Все значения уровня достоверности Р, соответствующие различным значениям t, можно найти в приложении любого статистического справочника.
При оценке разницы показателей, например I1 и I2 принято считать, что:
· если значение критерия tменьше 1,96 то, следовательно, показатели Р1 и Р2 различаются с уровнем доверия меньшим, чем 0,95 (P<0,95), а ошибка соответственно, больше 0,05 (р>0,05). В этом случае различие сравниваемых показателей признается статистически недостоверным, несущественным, обусловленным действием случайных факторов;
· если значение критерия tравно, или больше 1,96 то это означает, что показатели Р1 и Р2 различаются с уровнем доверия равным или большим, чем 0,95 (P>0,95) а, значение ошибки р<0,05. Такое различие показателей I1 и I2 признаётся статистически достоверным, неслучайным.
Внимание! Вывод о статистической достоверности различий еще не указывает, какова абсолютная и относительная выраженность различий показателей. Этот уровень доверия позволяет лишь (с известной долей ошибки) утверждать, что различие показателей не случайно, а обусловлено разной активностью (набором) объективных и (или) субъективных причин, определивших значения сравниваемых показателей.
При этом, если значение критерия t соответствует величине ошибки значительно меньшей, чем р<0,05, то рекомендуется привести точное значение р, или хотя бы указывать, что оно меньше 0,01 (для этого значения р критическая величина t=2,58). Такой прием уточняет, на сколько полученный результат измерения ошибки достоверности различий меньше принятой «точки отсечки - точки р=0,05».
Точно также если уровень ошибки больше 0,05, рекомендуется указать его точное значение, что бы читатель мог сам решить, как относиться к результатам исследования.
Например, если в результате оценки достоверности различий каких-либо величин получен критерий t = 5,6, то не следует ориентироваться на критические величины и обозначать ошибку как р<0,05. По крайней мере необходимо указать, что р< 0,001, такое значение ошибки существенно увеличит уверенность читателя в том, что полученные в исследовании результаты не случайны .
Или, если например получено значение t= 1,90, более правильным будет указать точное значение ошибки, т.е. р=0,0575, а не ограничится указанием, что р>0,05, ведь в данном случае результаты исследования совсем немного не «дотягивают» до критической точки, позволяющей отвергнуть нулевую гипотезу с 5% ошибкой.
Дата добавления: 2015-12-10; просмотров: 3783;