Основные законы динамики
Динамика – раздел теоретической механики, в котором изучаются законы движения материальных тел в пространстве с учетом действующих на них сил как причин тех или иных изменений в характеристике их движения. Основу динамики составляют законы (аксиомы) Галилея - Ньютона: закон инерции, закон пропорциональности силы и ускорения, закон равенства действия и противодействия, закон независимости действия сил.
1-ая аксиома динамики – закон инерции – материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения, если на нее (него) действует уравновешенная система, до тех пор, пока действие других тел не изменит это состояние. И наоборот, если нужно, чтобы точка (тело) двигались равномерно и прямолинейно, то необходимо создать условия для равновесия всех сил, приложенных к ней (нему).
Свойство материальных тел, заключающееся в стремлении их сохранять неизменным данное кинематическое состояние (покоя или движения), называетсяинерцией. Мерой инерции материальных тел являются: масса (при поступательном движении) или момент инерции (при вращении). Масса – количество материи в данной точке (в данном объеме), которое определяет инерционность тела только при его поступательном движении, так как в этом случае скорости и ускорения всех точек тела в данный момент времени равны.
При вращении вокруг оси инерционность тела определяется не только массой, но и ее распределением в окрестности вращения. Чем компактнее (ближе к оси) распределена масса тела, тем меньше инерционность тела и наоборот. Поэтому при вращении тела вокруг оси его инерционность определяет момент инерции тела.Различают моменты инерции тела относительно: точки (начала системы координат); оси (координатных осей); плоскости (координатных плоскостей). Момент инерции точкиравен произведению массы m точки на квадрат ее кратчайшего расстояния r до оси (центра) вращения: J =mr2, кг.м2. Момент инерции телаотносительно точки (оси, плоскости) – величина, равная предельному значению суммы произведений масс элементарных частиц тела на квадрат их кратчайшего расстояния до точки (оси, плоскости): J= limS mi ri2, кг . м2.
2-ая аксиома динамики – основной закон динамики ( 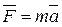 ) –ускорение материальной точки пропорционально приложенной к ней силе и имеет одинаковое с ней направление (рис. 3.1 а). Этот закон утверждает, во-первых, что причиной ускорения служит сила, во-вторых, что числовое значение ускорения пропорционально числовому значению силы и, в-третьих, что направление вектора ускорения всегда совпадает с направлением вектора силы.
) –ускорение материальной точки пропорционально приложенной к ней силе и имеет одинаковое с ней направление (рис. 3.1 а). Этот закон утверждает, во-первых, что причиной ускорения служит сила, во-вторых, что числовое значение ускорения пропорционально числовому значению силы и, в-третьих, что направление вектора ускорения всегда совпадает с направлением вектора силы.
|
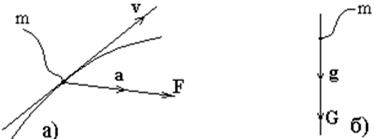
| Рис. 3.1. Движение точки по кривой - а; падение в поле тяжести – б. |
Законы инерции и пропорциональности силы и ускорения справедливы для инерциальных систем отсчета –систем отсчета, движущихся прямолинейно и равномерно друг относительно друга.
3-ья третья аксиома динамики – закон равенства действия и противодействия: при взаимодействии двух тел, силы приложенные к каждому из них, равны по модулю и направлены по одной прямой в противоположные стороны. | 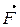 |=|
|=| 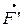 |,
|, 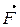 =
= 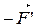 , где F – сила действия на данное тело со стороны другого тела,
, где F – сила действия на данное тело со стороны другого тела, 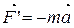 - сила противодействия телу со стороны другого тела (сила инерции
- сила противодействия телу со стороны другого тела (сила инерции 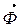 ),
), 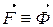 . Этот закон используется при определении взаимодействия как неподвижных (в статике), так и двигающихся тел (динамике). Сила инерции материальной точки – сила противодействия телу сообщающему точке ускорение
. Этот закон используется при определении взаимодействия как неподвижных (в статике), так и двигающихся тел (динамике). Сила инерции материальной точки – сила противодействия телу сообщающему точке ускорение 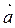 , равная:
, равная: 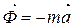 ,
, 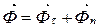 , где
, где 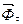 – касательная составляющая силы инерции, пропорциональная касательной составляющей at полного ускорения a точки;
– касательная составляющая силы инерции, пропорциональная касательной составляющей at полного ускорения a точки; 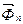 – нормальная составляющая силы инерции, пропорциональная нормальной составляющей
– нормальная составляющая силы инерции, пропорциональная нормальной составляющей 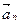 полного ускорения
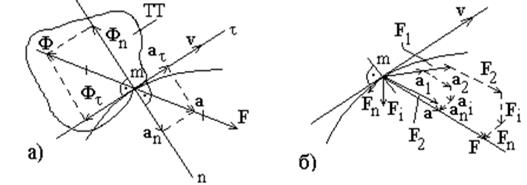
полного ускорения 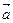 , см. рис. 3.2 а.
, см. рис. 3.2 а.
|
| Рис. 3.2. Сила действия и сила инерции (а); сложение ускорений (б). |
4-ая аксиома динамики – закон независимости действия сил: несколько одновременно действующих на материальную точку сил ( 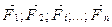 ) сообщают точке такое ускорение
) сообщают точке такое ускорение 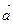 , какое сообщила бы ей одна сила
, какое сообщила бы ей одна сила 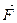 , равная их геометрической сумме
, равная их геометрической сумме 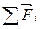 т.е.
т.е. 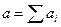 , где
, где 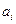 – ускорение точки, сообщаемое ей i-ой силой (рис. 3.2 б). Этот закон позволяет облегчить решение задач динамики: если на материальную точку действует несколько сил, то можно сначала найти ускорения, приобретенные от действия каждой силы отдельно, а затем эти ускорения геометрически сложить и найти ее полное ускорение.
– ускорение точки, сообщаемое ей i-ой силой (рис. 3.2 б). Этот закон позволяет облегчить решение задач динамики: если на материальную точку действует несколько сил, то можно сначала найти ускорения, приобретенные от действия каждой силы отдельно, а затем эти ускорения геометрически сложить и найти ее полное ускорение.
Дата добавления: 2015-12-08; просмотров: 3220;
