Примеры решения задач. Воздушный шар весом Р опускается с ускорением а
Задача 3.1.
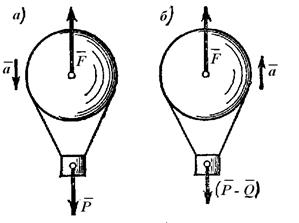
Воздушный шар весом Р опускается с ускорением а. Какой груз Q (балласт) надо сбросить, чтобы шар стал подниматься с таким же ускорением.
|
| Рис. 3.8. К задаче 3.1. |
Решение.
На падающий шар действуют сила тяжести 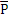 и подъемная сила
и подъемная сила 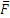 (рис.3.8). Составляя уравнение второй закон Ньютона в проекции на вертикаль, найдем, что
(рис.3.8). Составляя уравнение второй закон Ньютона в проекции на вертикаль, найдем, что
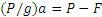 .
.
Когда будет сброшен балласт (рис. 3.8, б), вес шара станет равен 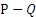 , а подъемная сила останется той же. Тогда, учитывая что шар при этом движется вверх, получим
, а подъемная сила останется той же. Тогда, учитывая что шар при этом движется вверх, получим
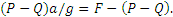
Исключая из этих уравнений неизвестную силу F, найдем
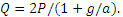
Задача 3.2.
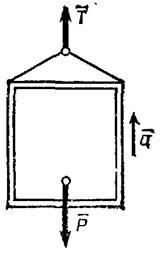
Лифт весом Р (рис. 3.9) начинает подниматься с ускорением а. Определить натяжение троса.
|
| Рис. 3.9. К задаче 3.2. |
Решение.
На лифт действуют сила тяжести 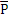 и реакция троса
и реакция троса 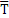 . Составляя второй закон Ньютона в проекции на вертикаль, получим
. Составляя второй закон Ньютона в проекции на вертикаль, получим 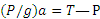 , откуда
, откуда
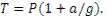
Если лифт опускается с таким же ускорением, то натяжение троса будет равно 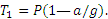
Задача 3.3.
Радиус закругления в точке А моста равен R (рис. 3.10). Найти, какое давление на мост в точке А окажет автомобиль массы m, движущийся со скоростью 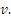
Решение.
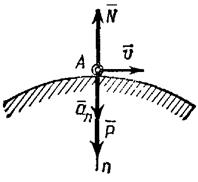
|
| Рис. 3.10. К задаче 3.3. |
В точке А автомобиль имеет нормальное ускорение 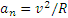 . При этом на него действуют сила тяжести
. При этом на него действуют сила тяжести 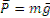 и реакция
и реакция 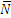 . Тогда по второму закону Ньютона, составленному в проекции на нормаль
. Тогда по второму закону Ньютона, составленному в проекции на нормаль 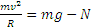 , откуда
, откуда 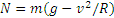 .
.
Сила давления на мост равна по модулю N, но направлена вниз.
Задача 3.4.
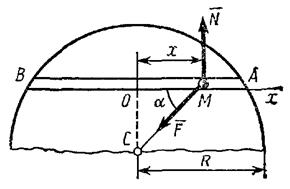
Пренебрегая трением и сопротивлением воздуха, определить, в течение какого промежутка времени тело пройдет по прорытому сквозь Землю вдоль хорды АВ каналу от его начала А до конца В (рис. 3.11). При подсчете считать радиус Земли R=6370 км.
|
| Рис. 3.11. К задаче 3.4. |
Решение.
В теории притяжения доказывается, что тело, находящееся внутри Земли, притягивается к ее центру с силой F, прямо пропорциональной расстоянию r до этого центра. Принимая во внимание, что при r=R (т. е. на поверхности Земли) сила F равна силе тяжести ( 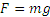 ), получим, что внутри Земли
), получим, что внутри Земли
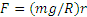 ,
,
где 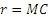 — расстояние от точки М до центра Земли.
— расстояние от точки М до центра Земли.
Поместим начало отсчета О в середине хорды АВ (в этой точке тело, находящееся в канале, было бы в равновесии) и направим ось Ох вдоль линии ОА. Если обозначить длину хорды АВ через 2а, то начальные
условия задачи будут: при t=0 x=a, 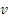 x=0.
x=0.
В произвольном положении на тело действуют силы 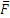 и
и 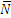 . Следовательно,
. Следовательно,
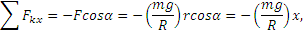
так как из чертежа видно, что 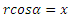 , Nx=0.
, Nx=0.
Действующая сила оказалась зависящей от координаты х точки М.Необходимо решить дифференциальное уравнение. Сокращая на 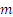 и вводя обозначение
и вводя обозначение
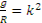 ,
,
получим
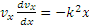 .
.
Умножая обе части этого равенства на 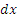 , сразу разделяем переменные и, интегрируя, находим
, сразу разделяем переменные и, интегрируя, находим
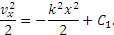
По начальным условиям при 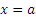
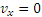 . Следовательно,
. Следовательно, 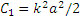 . Подставляя это значение С1, получаем
. Подставляя это значение С1, получаем
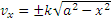 .
.
Считая, что в рассматриваемом положении скорость направлена от М к О, т. е. что 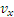 <0, берем перед корнем знак минус (легко, однако, проверить, что тот же окончательный результат получится и при знаке плюс). Тогда, заменяя
<0, берем перед корнем знак минус (легко, однако, проверить, что тот же окончательный результат получится и при знаке плюс). Тогда, заменяя 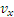 на
на 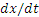 , найдем, что
, найдем, что
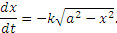
Разделяя переменные, приведем это уравнение к виду
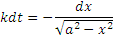
и, интегрируя, получим
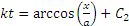 .
.
Подставляя сюда начальные данные (при 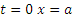 ), находим, что С2=0. Окончательно закон движения тела в канале будет иметь вид
), находим, что С2=0. Окончательно закон движения тела в канале будет иметь вид
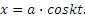
Следовательно, тело будет совершать в канале АВ гармонические колебания с амплитудой а.
Найдем теперь время t1 движения тела до конца В канала. В точке В координата 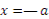 . Подставляя это значение в уравнение движения, получим
. Подставляя это значение в уравнение движения, получим 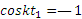 , откуда
, откуда 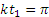 и
и 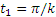 . Но по введенному обозначению
. Но по введенному обозначению 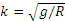 . Отсюда, произведя подсчет, находим, что время движения по каналу АВ при условиях задачи не зависит от его длины и всегда равно
. Отсюда, произведя подсчет, находим, что время движения по каналу АВ при условиях задачи не зависит от его длины и всегда равно
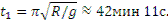
Этот очень интересный результат породил ряд (пока еще фантастических) проектов прорытия такого канала.
Найдем дополнительно, чему будет равна при движении максимальная скорость тела. Из выражения для 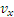 видно, что
видно, что 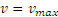 при х=0, т. е, в точке О.
при х=0, т. е, в точке О.
Следовательно,
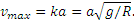
Если, например, 2а=0,1, R=637 км (приблизительно расстояние от Москвы до Санкт-Петербурга), то 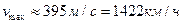 .
.
Задача 3.5.
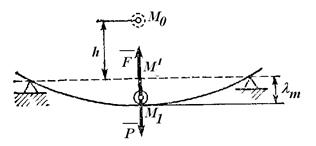
Груз, лежащий на середине упругой балки (рис. 3.12), прогибает ее на величину λст (статистический прогиб балки) Пренебрегая весом балки, определить, чему будет равен ее максимальный прогиб λm, если груз упадет на балку с высоты Н.
|
| Рис. 3.12. К задаче 3.5. |
Решение.
Воспользуемся для решения уравнением теоремой об изменении кинетической энергии. В данном случае начальная скорость груза 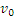 и конечная его скорость
и конечная его скорость 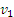 (в момент максимального прогиба балки) равны нулю и уравнение работа всех внешних сил равна нулю
(в момент максимального прогиба балки) равны нулю и уравнение работа всех внешних сил равна нулю
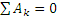
Работу здесь совершают сила тяжести 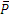 на перемещении М0М1 и сила упругости балки
на перемещении М0М1 и сила упругости балки 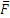 на перемещении M'M1. При этом
на перемещении M'M1. При этом 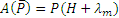 ,
, 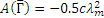 , так как для балки
, так как для балки 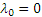 ,
, 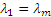 . Поэтому
. Поэтому
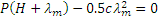 .
.
Но при равновесии груза на балке сила тяжести уравновешивается силой упругости, следовательно, 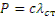 и предыдущее равенство можно представить в виде
и предыдущее равенство можно представить в виде 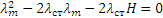
Решая это квадратное уравнение и учитывая, что по условиям задачи должно быть 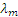 >0, находим
>0, находим
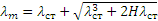 .
.
Интересно отметить, что при Н=0 получается 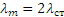 . Следовательно, если груз положить на середину горизонтальной балки, то ее максимальный прогиб при опускании груза будет равен удвоенному статическому. В дальнейшем груз качнет вместе с балкой совершать колебания около равновесного положения. Под влиянием сопротивлений эти колебания затухнут и система уравновесится
. Следовательно, если груз положить на середину горизонтальной балки, то ее максимальный прогиб при опускании груза будет равен удвоенному статическому. В дальнейшем груз качнет вместе с балкой совершать колебания около равновесного положения. Под влиянием сопротивлений эти колебания затухнут и система уравновесится
в положении, при котором прогиб балки равен 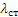 .
.
Задача 3.6.
Груз весом Р, подвешенный на нити длиной 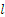 , отклоняют от вертикали на угол α в положение М0 и отпускают без начальной скорости. Определить натяжение нити в момент, когда груз дойдет до наинизшего положения М1.
, отклоняют от вертикали на угол α в положение М0 и отпускают без начальной скорости. Определить натяжение нити в момент, когда груз дойдет до наинизшего положения М1.
Решение.
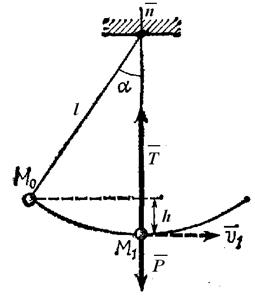
|
| Рис. 3.13. К задаче 3.6. |
Изображаем груз в том положении, для которого надо найти натяжение нити, т. е. в положении М1 (рис. 3.13). На груз действуют сила тяжести 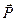 и сила реакции нити
и сила реакции нити 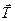 . Проводим нормаль М1n в сторону вогнутости траектории и составляем второй закон Ньютона, учитывая, что в нашем случае радиус равен l. Получим
. Проводим нормаль М1n в сторону вогнутости траектории и составляем второй закон Ньютона, учитывая, что в нашем случае радиус равен l. Получим
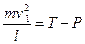 или
или 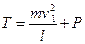 ,
,
Где 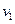 — скорость груза в положении М1. Для определения
— скорость груза в положении М1. Для определения 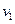 воспользуемся теоремой об изменении кинетической энергии
воспользуемся теоремой об изменении кинетической энергии
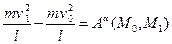
Работу на участке М0М1 совершает только сила 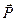 . Поэтому
. Поэтому 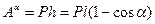 .
.
Так как 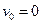 , то, подставляя найденное значение работы в теорему об изменении кинетической энергии, получим
, то, подставляя найденное значение работы в теорему об изменении кинетической энергии, получим 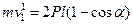 и окончательно найдем
и окончательно найдем
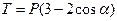 .
.
В частном случае, если угол начального отклонения α=90°, натяжение нити при прохождении через вертикаль будет равно 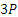 , т. е. утроенному весу груза.
, т. е. утроенному весу груза.
Полученное решение показывает, что динамические реакции действительно могут значительно отличаться от статических.
Задача 3.7 (рис.3.14).
Тело движется из точки А по участку АВ длиной L=10 м наклонной плоскости, составляющей угол 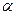 =300 с горизонтом в течение
=300 с горизонтом в течение 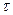 секунд. Начальная скорость равна нулю. Коэффициент трения скольжения тела по плоскости равен
секунд. Начальная скорость равна нулю. Коэффициент трения скольжения тела по плоскости равен 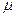 =0,2.
=0,2.
В точке В тело покидает плоскость и попадает в точку С плоскости ВС, наклоненной под углом 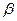 =600 к горизонту.
=600 к горизонту.
При решении задачи принять тело за материальную точку, сопротивление воздуха не учитывать, Принять 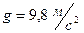
Определить 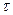 и h.
и h.
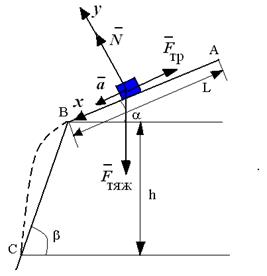
|
| Рис. 3.14. К задаче 3.7. |
Решение.
Часть 1
На участке АВ действуют: сила тяжести, сила реакции опоры и сила трения.
Составим второй закон Ньютона в векторном виде
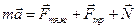
В проекциях на оси координат
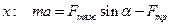
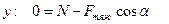
Так как сила трения 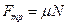 , поэтому
, поэтому
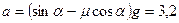 м/с.
м/с.
Применяя формулы кинематики
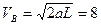 м/с
м/с 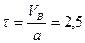 с
с
Часть 2
На участке BC на тело действует только сила тяжести, поэтому оно имеет ускорение g и направлено вертикально вниз. Движение по горизонтали равномерное, по вертикали – равноускоренное. Поэтому
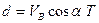
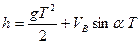
Из рис. 3.14. видно, что 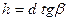
Решив полученную систему уравнений
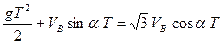
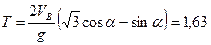 с.
с.
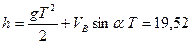 м
м
Ответ 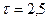 с;
с; 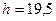 м.
м.
Задача 3.8.
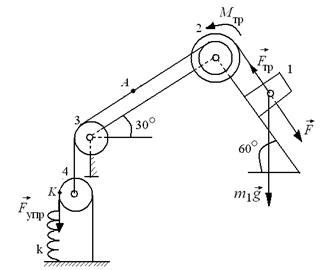
Механическая система состоит из (рис.3.8):
· Груза 1 массой m1=8 кг
· Невесомого ступенчатого шкива 2 с радиусами ступеней R2=0,3 м, r2=0,1 м.
· Блока 3 радиусом R3=0,2 м и массой m3=4 кг, масса блока равномерно распределена по ободу.
· Подвижного блока 4 массой 18 кг, который представляет собой сплошной однородный цилиндр
· Пружины жесткости k=3200 Н/м
Тела системы соединены друг с другом нитями. Коэффициент трения грузов о плоскость 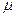 =0,1. Под действием силы F=50(8+3s), зависящей от перемещения s первого груза, система приходит в движение из состояния покоя. Деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М=12 Нм сил сопротивления (от трения в подшипниках). Найти скорость первого груза в тот момент времени, когда его перемещение s=0,2 м.
=0,1. Под действием силы F=50(8+3s), зависящей от перемещения s первого груза, система приходит в движение из состояния покоя. Деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М=12 Нм сил сопротивления (от трения в подшипниках). Найти скорость первого груза в тот момент времени, когда его перемещение s=0,2 м. 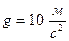
Решение
|
| Рис. 3.15. К задаче 3.8. |
Вычислим кинетическую энергию заданной системы грузов как функцию скорости первого тела.
Груз 1 движется поступательно, поэтому его кинетическая энергия 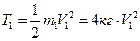
Кинетическая энергия ступенчатого шкива 2 равна нулю, так как он невесом. Угловая скорость шкива 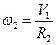 .
.
Скорость точки А 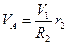 .
.
Кинетическая энергия блока 3 - 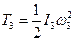 , где
, где 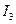 - его момент инерции, который в данном случае равен
- его момент инерции, который в данном случае равен 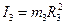 . Угловая скорость блока 3
. Угловая скорость блока 3 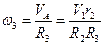 . В итоге кинетическая энергия
. В итоге кинетическая энергия 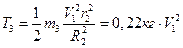
Центр подвижного блока 4 движется со скоростью 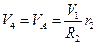 . Угловая скорость его вращения
. Угловая скорость его вращения 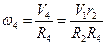 , где
, где 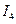 - его момент инерции, который для сплошного цилиндра равен
- его момент инерции, который для сплошного цилиндра равен 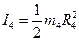 . Кинетическая энергия состоит из двух слагаемых – поступательного и вращательного движений. В итоге
. Кинетическая энергия состоит из двух слагаемых – поступательного и вращательного движений. В итоге 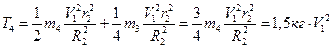
Кинетическая энергия системы
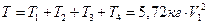
Найдем работу внешних сил
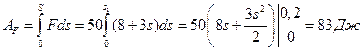
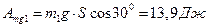
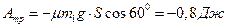
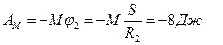
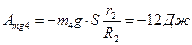
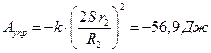 , так как скорость точки K определяется с помощью формулы
, так как скорость точки K определяется с помощью формулы 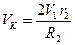 .
.
В итоге, работа всех внешних сил 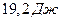
Так как работа внешних сил равна изменению кинетической энергии, поэтому V1 = 1,35 м / с.
Дата добавления: 2015-12-08; просмотров: 5195;
