Динамика материальной точки

Точка, движение которой ничем не ограничено, называется свободной. Свободная точка под действием приложенных сил может двигаться в каком угодно направлении. Примером такого движения может служить так называемое свободное падение – движение точки под действием силы тяжести в безвоздушном пространстве (рис. 3.1 б). 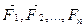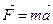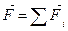Задачи, в которых рассматривается свободная точка, на которую действует несколько сил , решаются при помощи основного уравнения динамики , где – равнодействующая. При этом согласно закону независимости действия сил, 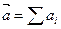, т.е. ускорение точки равно геометрической сумме ускорений, сообщенных ей каждой силой в отдельности (см.рис.3.2 б). При движения точки в плоскости или пространстве векторное равенство заменяется двумя или тремя скалярными дифференциальными уравнениями для проекций на оси декартовой и естественной систем координат соответственно:

m x^{``</sup>= SF<sub>i х</sub>, my<sup>``}= SF_{i у}, mz^``=SF_{i z};

m 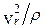= SF_{i n}, m 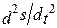= SF_{i r}.

При несвободном движении точки, например, по плоской неподвижной шероховатой кривой (твердой поверхности) в правой части дифференциальные уравнений ( ), кроме активных сил, будут содержать еще проекции на оси систем координат (или касательной и нормальной составляющих) полной силы реакции этой (поверхности) как связи.

В динамике материальной точки решаются две основные задачи: прямая и обратная. Прямая задача динамики точки – задача об определении движения точки по заданным силам. Обратная задача динамики точки – задача об определении сил по заданному движению точки. При решении этих задач исходными являются дифференциальные уравнения движения точки, записанные в общем виде в декартовых или естественных координатах.

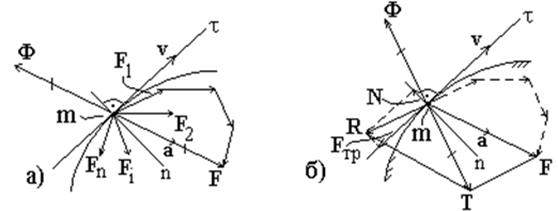
Ряд задач динамики материальной точки решается с помощью принципа Даламбера, который формулируется следующим образом: движущаяся свободная материальная точка может рассматриваться как покоящаяся под действием активных (заданных) сил и сил инерции, т.е. 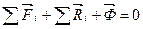– условие псевдопокоя свободной точки под действием сил, сходящихся в точке (рис. 3.3а). Для несвободной материальной точки (рис.3.3б) принцип Даламбера формулируется следующим образом: движущаяся несвободная материальная точка может рассматриваться как покоящаяся под действием активных сил, реакций связи и силы инерции, т.е. 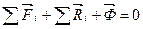– условие псевдопокоя несвободной точки под действием сил, сходящихся в точке.

Рис. 3.3. Применение принципа Даламбера для свободной (а) и несвободной (б) точки.

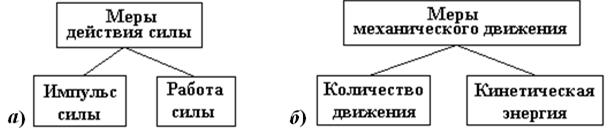
Различают две меры действия силы и механического движения векторная и скалярная (рис. 3.4).

Рис. 3.4. Меры действия силы (а) и механического движения (б).

Импульс силы – вектор 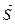, динамическая величина, характеризующая передачу материальной точке механического движения со стороны действующего на нее тела за данный промежуток Dt времени, и учитывающая (в отличие от силы) и интенсивность, и продолжительность механического взаимодействия. Импульс постоянной по величине и направлению силы равен произведению вектора силы на интервал времени ее действия, 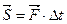, Hм. Импульс переменной по величине и (или) направлению силы равен: S = 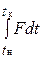, Dt = t_к – t_н – время действия силы 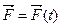, где t_н и t_к – моменты начала и конца ее действия.

Работа силы – алгебраическая величина, характеризующая передачу точке (телу) механического движения со стороны действующего на нее тела (точки) при перемещении точки (тела) на некотором пути. Работа силы 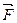, постоянной по величине и направлению, на конечном перемещении 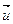материальной точки равна скалярному произведению вектора силы на вектор перемещения:
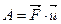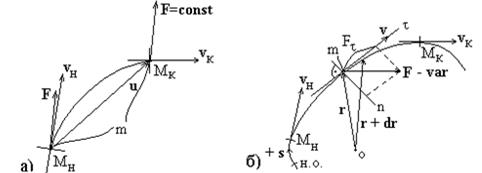
= | F|^.|u|cos( 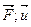) (рис. 3.5 а). Работа силы 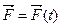, переменной по величине и (или) направлению, на конечном перемещении материальной точки равна значению криволинейного интеграла взятого от выражения для элементарной работы этой силы на элементарном перемещении радиуса-вектора точки 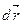: 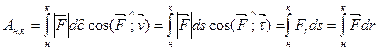(рис. 3.5 б), где 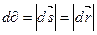– элементарный путь, пройденный точкой за элементарный интервал времени dt; ds – элементарное приращение дуговой координаты точки ; 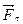– проекция силы на орт касательной 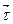к траектории в данной точке.

Рис. 3.5. Определение работы для постоянной (а) и переменной (б) силы.

Мощность N постоянной силы – отношение элементарного приращения работы dA силы F к элементарному интервалу времени dt, в течении которого имело место это приращение, т.е. – работа совершаемая в единицу времени:

.

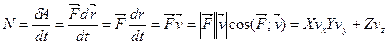Работа равнодействующей силы 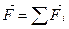на некотором перемещении равна алгебраической сумме работ ее составляющих ( 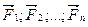) на том же перемещении: 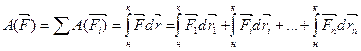. Работа постоянной силы

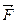на результирующем перемещении 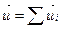равна алгебраической сумме работ этой силы на составляющих ( 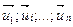) перемещения .

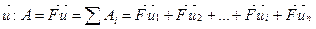Импульс 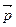материальной точки – вектор, имеющий направление вектора скорости 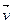и модуль, равный произведению массы точки на модуль скорости ее движения: 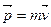, 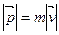(рис. 3.6а).

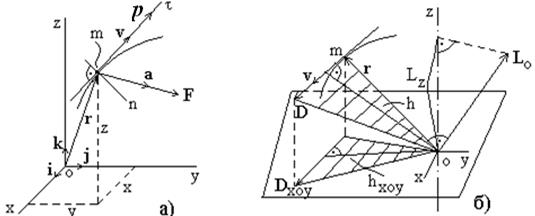
Рис. 3.6. Импульс p (а) и момент импульса L (б) материальной точки.

Производная от вектора импульса 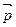точки по времени равна равнодействующей всех сил, действующих на точку: 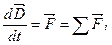. Приращение вектора импульса 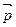точки за конечный интервал времени равно геометрической сумме импульсов всех сил, действующих на точку в течении этого интервала времени:

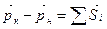или 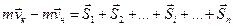или в проекциях на оси декартовой системы координат, получим: mv_KX - mv_HX = åS_Xi ; mv_KY - mv_HY = åS_Yi; mv_KZ - mv_HZ = åS_zi. В случае, когда 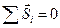или, например 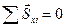, выполняется закон сохранения импульс материальной точки в целом ( 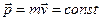) или в проекции на ось, x (р_x = mv_x = const).

Момент импульса материальной точки относительно центра О – вектор 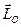, направленный перпендикулярно плоскости, проходящей через вектор 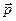этой точки и центр О в ту сторону, смотря откуда вектор 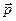виден направленным против вращения часовой стрелки, и равный: 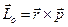(рис. 3.6 б). Момент импульса материальной точки относительно оси – алгебраическая величина, взятая со знаком плюс или минус, и равная произведению модуля проекции р_xOy вектора импульса 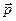на плоскость xOy, перпендикулярную оси z, на плечо h_xOy этой проекции относительно этой оси z: L_z =|р_xOy| h_xOy (рис.3.6 б).

Производная от вектора момента импульса относительно центра по времени равна главному моменту всех сил, действующих на точку, относительно этого центра: 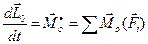или в проекциях на оси декартовой системы координат, получаются соотношения: 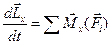; ; 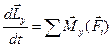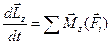, которые выражают теорему об изменении момента импульса точки, записанную в дифференциальной векторной и аналитической формах соответственно. В случае, когда 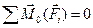или, например 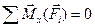, выполняется закон сохранения момента импульса точки относительно центра ( 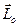) или оси (L_x ).

Кинетическая энергия точки – мера механического движения, равная половине произведения массы точки на квадрат скорости ее движения: K =(1/2)mv²_.
Приращение кинетической энергии K материальной точки при ее движении на некотором пути равно сумме работ всех сил, действующих на точку на этом пути: DK = åA_i , где DK = K_K - K_H, K_K , K_H – кинетическая энергия точки в конечном и начальном положениях.