Кинематика плоскопараллельного движения твердого тела
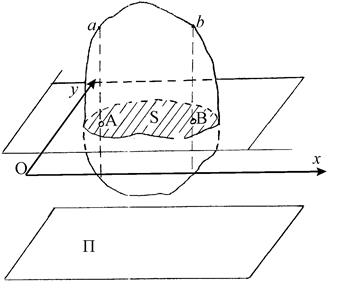
Плоскопараллельным (плоским) движением твердого тела называется такое движение, при котором траектории всех его точек лежат в плоскостях, параллельных некоторой неподвижной плоскости П (рис. 2.2). При пересечении тела плоскостью хОу, параллельной этой плоскости, в его сечении получится какая-то плоская фигура S, которая будет перемещаться при движении тела, оставаясь все время в той же плоскости хОу. При таком движении все точки
|
| Рис. 2.2. Плоскопараллельное (плоское) движение твердого тела. |
тела, лежащие на перпендикуляре Аа к плоскости фигуры, движутся совершенно одинаково, так же как и точка А этой фигуры. Все точки, расположенные на перпендикуляре Вв к плоскости фигуры, движутся так же, как и точка В этой фигуры, и т.д. (рис. 2.2). Поэтому для определения плоского движения тела достаточно знать движение этой фигуры в ее плоскости S.
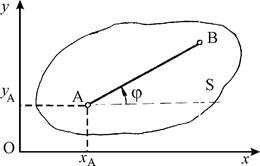
Положение неизменяемой плоскости S вполне определяется положением двух произвольных ее точек А и В. Следовательно, изучение движения этой фигуры сводится к изучению движения прямолинейного отрезка АВ в плоскости этой фигуры. Положение этого отрезка определяется двумя координатами хА и уА точки А, называемой полюсом и углом j, который образует этот отрезок с некоторой осью неизменного направления, лежащей в плоскости данной фигуры (рис. 2.3). Таким образом, движение плоской фигуры в ее плоскости можно определить тремя уравнениями, из которых следует, что движение плоской фигуры можно разложить на два движения:1) поступательное движение вместе с полюсом А, определяемое уравнениями: xA= хA(t), yA=yA (t) и 2) вращательное движение вокруг полюса, определяемое уравнением: j =j(t).
|
| Рис. 2.3. Положение отрезка АВ, с которым неизменно связана фигура S. |
При этом угловая скорость вращательного движения не зависит от выбора полюса. Поэтому скорость любой точки В этой фигуры равна геометрической сумме скорости полюса 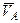 и скорости
и скорости 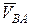 точки В во вращательном движении вокруг него (рис. 16), т. е.
точки В во вращательном движении вокруг него (рис. 16), т. е. 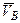 =
= 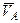 +
+ 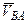 , причем
, причем 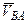 ^ АВ и
^ АВ и  = w×АВ. Отсюда следует теорема о проекциях скоростей точек плоской фигуры: проекции скоростей двух точек на ось h, проходящую через эти точки, равны между собой.
= w×АВ. Отсюда следует теорема о проекциях скоростей точек плоской фигуры: проекции скоростей двух точек на ось h, проходящую через эти точки, равны между собой.
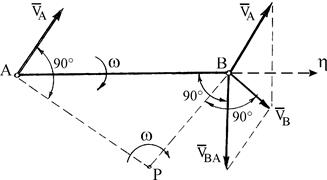
Мгновенным центром скоростей (МЦС) называется такая точка Р плоской фигуры, скорость которой в данный момент равна нулю. Если известны скорость 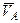 какой-либо точки А плоской фигуры и угловая скорость w этой фигуры, то, повернув вектор
какой-либо точки А плоской фигуры и угловая скорость w этой фигуры, то, повернув вектор 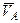 вокруг точки А на угол 90°в направлении вращения фигуры и отложив на этой полупрямой отрезок АР =
вокруг точки А на угол 90°в направлении вращения фигуры и отложив на этой полупрямой отрезок АР = 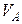 /w, получим точку Р, которая является МЦС (рис. 2.4).
/w, получим точку Р, которая является МЦС (рис. 2.4).
Если же известны направления скоростей двух точек плоской фигуры, то МЦС находят как точку пересечения перпендикуляров, восстановленных в этих точках к направлениям их скоростей. Если известны МЦСи угловая скорость фигуры, то вектор скорости 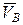 любой точки В фигуры - ее скорость во вращательном движении вокруг МЦС - перпендикулярна к отрезку РВ и по модулю равен w×РВ. Отсюда следует, что скорости точек плоской фигуры пропорциональны их расстояниям от мгновенного центра скоростей, т. е.
любой точки В фигуры - ее скорость во вращательном движении вокруг МЦС - перпендикулярна к отрезку РВ и по модулю равен w×РВ. Отсюда следует, что скорости точек плоской фигуры пропорциональны их расстояниям от мгновенного центра скоростей, т. е. 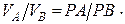
|
| Рис. 2.4. Определение мгновенного центра скоростей. |
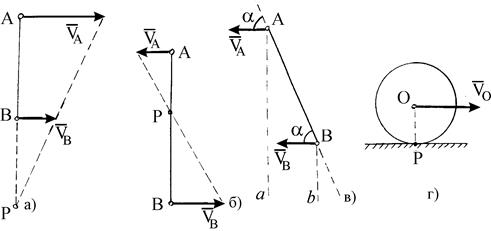
Отметим другие случаи нахождения положения МЦС, применяемые при решении задач. Если скорости точек А и В параллельны и АВ ^ 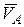 , то для определения положения МЦС следует воспользоваться свойством пропорциональности скоростей расстояниям точек до МЦС (рис. 2.5 а и б). Если скорости
, то для определения положения МЦС следует воспользоваться свойством пропорциональности скоростей расстояниям точек до МЦС (рис. 2.5 а и б). Если скорости 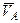 и
и 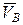 параллельны, но скорость
параллельны, но скорость 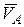 неперпендикулярна отрезку АВ (рис.2.5 в ), то прямые Аа и Вв, перпендикулярные
неперпендикулярна отрезку АВ (рис.2.5 в ), то прямые Аа и Вв, перпендикулярные 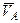 и
и 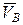 , пересекаются в бесконечности и мгновенного центра скоростей не существует, и угловая скорость фигуры равна нулю (w =0). На основании теоремы о проекциях скоростей VA×cosa =VB×cosa, отсюда VA=VB и
, пересекаются в бесконечности и мгновенного центра скоростей не существует, и угловая скорость фигуры равна нулю (w =0). На основании теоремы о проекциях скоростей VA×cosa =VB×cosa, отсюда VA=VB и 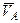 =
= 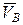 , т.е. в данный момент времени скорости всех точек плоской фигуры равны по модулю и направлению.
, т.е. в данный момент времени скорости всех точек плоской фигуры равны по модулю и направлению.
При качении без скольжения одного тела по поверхности неподвижного другого (рис. 2.5 г) МЦС совпадает с точкой Р соприкосновения тел (так как при отсутствии скольжения скорость точки соприкосновения равна нулю).
|
| Рис. 2.5. Методы нахождения положения МЦС, применяемые при решении задач. |
Ускорение любой точки плоской фигуры можно определить как геометрическую сумму ускорений этой точки в поступательном движении вместе с некоторым полюсом и вращательным движением вокруг этого полюса. Если известны ускорение 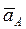 некоторой точки А фигуры (полюса), а также угловая скорость w и угловое ускорение e фигуры, то ускорение любой ее точки В определяется по формуле:
некоторой точки А фигуры (полюса), а также угловая скорость w и угловое ускорение e фигуры, то ускорение любой ее точки В определяется по формуле: 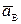 =
= 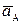 +
+ 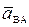 =
= 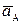 +
+ 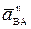 +
+ 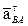 , где вектор
, где вектор 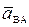 - ускорение точки В во вращательном движении вокруг полюса А;
- ускорение точки В во вращательном движении вокруг полюса А; 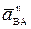 и
и 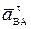 - нормальная и касательная составляющие этого вектора, которые вычисляются по формулам:
- нормальная и касательная составляющие этого вектора, которые вычисляются по формулам: 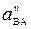 = w2×АВ,
= w2×АВ, 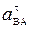 =e×АВ. При этом вектор
=e×АВ. При этом вектор 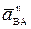 направлен вдоль отрезка ВА, а вектор
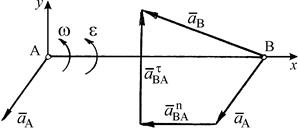
направлен вдоль отрезка ВА, а вектор 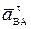 перпендикулярен к ВА (рис. 2.6). Ускорение точки В можно определить, если спроецировать векторное равенство:
перпендикулярен к ВА (рис. 2.6). Ускорение точки В можно определить, если спроецировать векторное равенство: 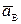 =
= 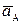 +
+ 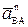 +
+ 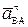 на оси х и у (см. рис. 2.6) и найти проекции этого ускорения:
на оси х и у (см. рис. 2.6) и найти проекции этого ускорения: 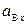 =
= 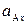 –
– 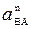 ,
, 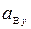 =
= 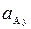 +
+ 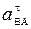 . По проекциям находят модуль ускорения точки В по формуле:
. По проекциям находят модуль ускорения точки В по формуле: 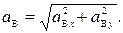
|
Рис. 2.6. Определение ускорения любой точки В фигуры ( 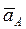 - ускорение полюса А). - ускорение полюса А).
|
Вопросы для самоконтроля
1. Какое движение твердого тела называется плоскопараллельным?
2. Какими уравнениями задается плоскопараллельное движение?
3. Как по уравнениям движения плоской фигуры найти скорость полюса и угловую скорость вращения вокруг полюса?
4. Как определить скорость любой точки плоской фигуры?
5. Сформулируйте теорему о проекциях скоростей двух точек плоской фигуры.
6. Что называется мгновенным центром скоростей плоской фигуры и как найти его положение в различных случаях?
7. Сформулируйте теорему об ускорениях точек плоской фигуры.
Дата добавления: 2015-12-08; просмотров: 2587;
