Составное (сложное) движение точки

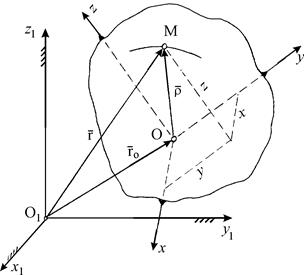
Составное движение точки - это движение, при котором точка одновременно участвует в нескольких движениях. Рассмотрим тело А (рис. 2.7), которое свободно движется по отношению к неподвижной системе координат О₁x₁y₁z₁. Пусть точка М совершает движение по поверхности этого тела. Через произвольную точку О движущегося тела проведем неизменно связанные с этим телом оси x,y,z. Систему осей Оxyz называют подвижной системой отсчета. Движение точки М по отношению к неподвижной системе отсчета называют ее абсолютным движением, которое характеризуется изменением ее радиуса-вектора 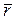, абсолютной скорости 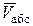и абсолютного ускорения 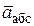(по модулю и направлению).

Рис. 2.7. Составное движение материальной точки.

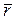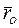Движение точки М по отношению к подвижной системе отсчета называют относительным движением точки, которое при неизменных радиусах-векторах и характеризуется изменением только ее радиуса-вектора 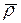, т.е относительной скоростью 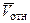и относительным ускорением 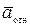в этой системе отсчета.

Движение подвижной системы отсчета Оxyz и неизменно связанного с ней тела А по отношению к неподвижной системе отсчета О₁x₁y₁z₁ является для точки М переносным движением. Переносное движение точки М при неизменном по модулю радиусе-векторе 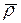характеризуется изменением радиусов-векторов 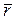и 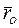(по модулю и направлению) , переносной скоростью 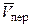и переносным ускорением 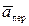точки М.

Таким образом, для изучения относительного или переносного движения точки следует мысленно остановить соответственно переносное или относительное движение и определить далее характеристики движения точки по формулам кинематики точки в абсолютном движении. Если точка М участвует в составном движении, то имеют место следующие теоремы: абсолютная скорость точки равна геометрической сумме переносной и относительной скоростей точки, т. е. 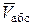= 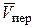+ 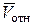; абсолютное ускорение точки равно геометрической сумме переносного, относительного и кориолисова (поворотного) ускорений этой точки, т. е. 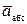= 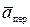+ + 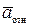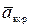, или = + + + + .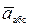

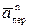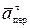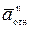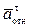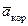Кориолисово ускорение 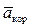равно удвоенному векторному произведению угловой скорости переносного вращения на относительную скорость точки, т. е.

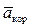=2×( 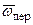´ 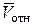). Следовательно, модуль этого ускорения 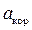=2×w_пер ×V_отн ×sin a, где a - угол между векторам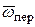и и 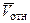.Чтобы найти направление кориолисова ускорения 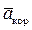точки М, достаточно в точке М построить векторы 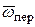и 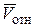и восстановить из этой точки перпендикуляр к плоскости, в которой лежат эти векторы 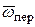и 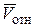. Вектор 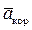направлен по этому перпендикуляру так, чтобы наблюдатель, смотрящий с конца этого вектора, видел поворот вектора 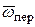на угол a против хода часовой стрелки до совмещения его с вектором 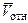(рис. 2.8).

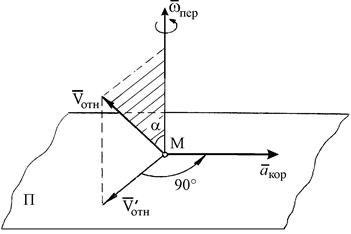
Рис. 2.8. Определение направление вектора кориолисова ускорения .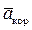

Направление вектора 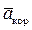можно определить и другим способом (правило Н. Е. Жуковского): если провести через точку М плоскость П, перпендикулярную к вектору 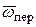и повернуть проекцию 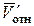относительной скорости 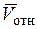на эту плоскость на 90° вокруг точки М в направлении переносного вращения, то получим направление вектора 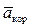(рис. 2.8).

Вопросы для самоконтроля

1. Что понимается под составным (сложным) движением точки?

2. Что называется абсолютным, переносным и относительным движением точки?

3. Сформулируйте, что такое переносная скорость и переносное ускорение точки.

4. В чем заключается теорема об абсолютной скорости точки, совершающей составное движение.

5. Сформулируйте теорему об ускорении точки в составном движении.

6. Как определить модуль и направление кориолисова ускорения точки?

7. В каких случаях ускорение Кориолиса равно нулю?