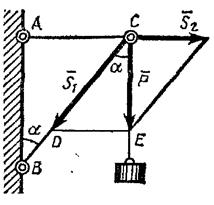
Примеры решения задач. Кронштейн состоит из стержней АС и ВС, соединенных со стеной и друг с другом шарнирами, причем , (рис.1.13)

Рис. 1.13. К задаче 1.1.

Задача 1.1.

Кронштейн состоит из стержней АС и ВС, соединенных со стеной и друг с другом шарнирами, причем 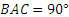, 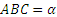(рис.1.13). В точке С подвешен груз весом Р. Определить усилия в стержнях, пренебрегая их весом.

Решение.

Под усилиями в стержнях понимают значения сил, растягивающих или сжимающих эти стержни. Так как стержни считаются невесомыми, то их реакции (они действуют на шарнир С) направлены вдоль стержней. Тогда для определения искомых усилий приложим силу 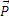в точке С и разложим ее по направлениям АС и СВ. Составляющие 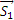и и 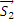будут искомыми силами. Из треугольника CDE находим:

, .

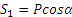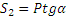Таким образом, стержень ВС сжимается силой S₁ а стержень АС растягивается силой S₂. С увеличением угла α усилия в стержнях растут и при а, близком к 90°, могут достигать очень больших размеров.

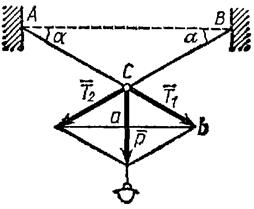
Рис. 1.14. К задаче 1.2.

Задача 1.2.

Фонарь весом Р=200 Н (рис. 1.14) подвешен на двух тросах АС и ВС, образующих с горизонтальной прямой одинаковые углы α=5°. Определить, с какой силой натянуты тросы.

Решение.

Приложим силу 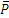в точке С и разложим ее по направлениям тросов. Параллелограмм сил в данном случае будет ромбом; диагонали его взаимно перпендикулярны и делятся в точке пересечения пополам. Из треугольника aCb находим, что Р/2=Т₁sinα. Тогда

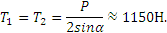
Из полученной формулы видно, что с уменьшением угла а натяжение тросов значительно увеличивается (например, при α= 1° T=5730 Н). Натянуть трос так, чтобы он стал горизонтальным, практически нельзя, так как при α→0 T→∞.

Задача 1.3

Груз весом Р лежит на гладкой наклонной плоскости с углом наклона α, (рис. 1.15, а). Определить значение горизонтальной силы 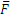, которую надо приложить к грузу, чтобы удержать его в равновесии, и найти, чему при этом равна сила давления 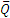груза на плоскость.

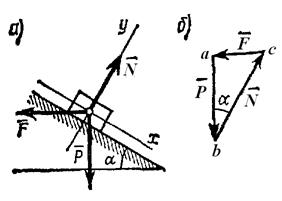
Рис. 1.15. К задаче 1.3.

Решение.

Искомые силы действуют на разные тела: сила 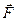на груз, сила 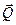— на плоскость. Для решения задачи вместо силы 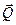будем искать равную ей по модулю, но противоположно направленную реакцию плоскости 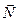. Тогда заданная сила 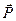и искомые силы 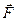и 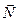будут действовать на груз, т. е. на одной то же тело. Рассмотрим равновесие груза и изобразим действующие на этот груз силы 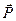и и 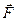реакцию связи 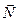. Для определения искомых сил можно воспользоваться или геометрическим, или аналитическим условиями равновесия. Рассмотрим оба способа решения.

Геометрический способ. При равновесии треугольник, построенный из сил 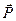, 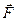и 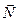, должен быть замкнутым. Построение треугольника начинаем с заданной силы. От произвольной точки а в выбранном масштабе откладываем силу 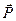(рис. 1.15, б). Через начало и конец этой силы проводим прямые, параллельные направлениям сил 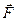и 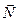. Точка пересечения этих прямых дает третью вершину с замкнутого силового треугольника abc, в котором стороны bc и са равны в выбранном масштабе искомым силам. Направление сил определяется правилом стрелок: так как здесь равнодействующая равна нулю, то при обходе треугольника острия стрелок нигде не должны встречаться в одной точке.

Модули искомых сил можно из треугольника abc найти и путем численного расчета (в этом случае соблюдать масштаб при изображении сил не надо). Замечая, что 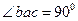, a 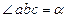, получим:

.

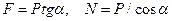Аналитический способ. Так как система действующих сходящихся сил является плоской, для нее надо составить два условия равновесия (12). Сначала проводим координатные оси; при этом для получения более простых уравнений ось 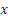направляем перпендикулярно неизвестной силе 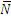. Далее вычисляем проекции сил 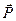, , 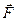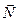на оси x и у, внося их в таблицу :

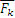
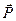
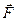
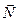
Fkx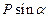
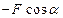
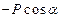
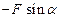
Fky			N

Теперь составляем уравнения 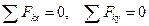. Получим:

,

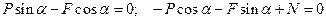Решая эти уравнения, найдем:

.

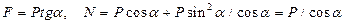Геометрическое решение в подобных простых задачах (когда действующих cил три) оказывается более компактным, чем аналитическое. Как видно, при 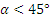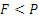, а при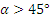 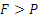; 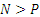при любом .

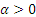Искомая сила давления груза на плоскость численно равна N, но направлена в противоположную сторону ( =— ).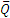

Задача 1.4

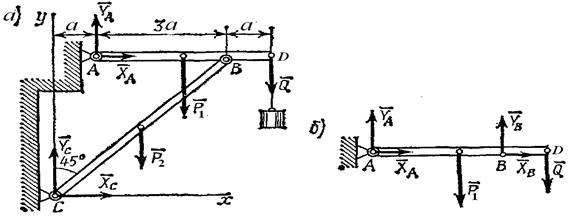
Кронштейн состоит из горизонтального бруса AD (рис. 1.16) весом Р₁=150 Н, прикрепленного стене шарниром, и подкоса СВ весом Р₂=120 Н, который с брусом AD и со стеной также соединен шарнирами (все размеры показаны на чертеже). К концу D бруса подвешен груз весом Q=300 H. Определить реакции шарниров А и С, считая брус и подкос однородными.

Рис. 1.16. К задаче 1.4.

Решение.

Рассмотрим сначала равновесие всего кронштейна. На него действуют следующие внешние силы: заданные силы 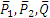и реакции связей 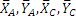. Кронштейн, освобожденный от внешних связей, не образует

жесткой конструкции (брусья могут поворачиваться вокруг шарнира В), но по принципу отвердевания действующие на него силы при равновесии должны удовлетворять условиям равновесия статики.

Составляя эти условия, найдем:

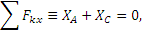
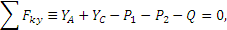
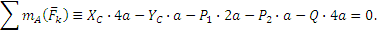
Полученные три уравнения содержат, как видим, четыре неизвестных Х_А, Y_A, X_C, Y_C. Для решения задачи рассмотрим дополнительно равновесие бруса АD (рис. 1.16, б). На него действуют силы 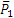, , 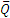реакции 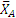, 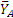реакции 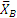, которые для бруса AD (когда рассматривается его равновесие) будут силами внешними. Недостающее четвертое уравнение составим, беря моменты действующих на брус AD сил относительно центра В (тогда в уравнение не войдут новые неизвестные Х_B, Y_B):

Решая теперь систему четырех составленных уравнений (начиная с последнего), найдем:

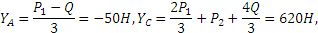
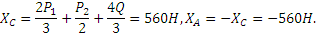
Из полученных результатов видно, что силы 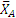и 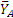имеют направления, противоположные показанным на чертеже. Реакции шарнира В, если их надо определить, найдутся из уравнений проекций на оси х и у сил, действующих на брус AD, и будут равны: Х_B=— Х_А, Y_B=P₁+Q—Y_A=500 H.

Как видим, при решении задач статики не всегда надо составлять все условия равновесия для рассматриваемого тела. Если в задаче не требуется определять реакции некоторых связей, то надо пытаться сразу составить такие уравнения, в которые эти неизвестные реакции не будут входить. Так мы и поступили в данной задаче при рассмотрении равновесия бруса AD, составляя только одно уравнение моментов относительно центра В.

Задача 1.5

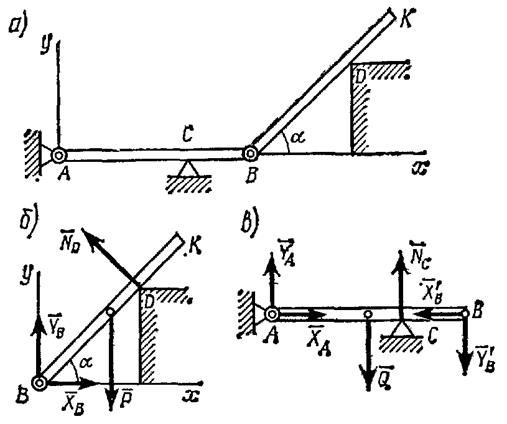
Горизонтальная балка АВ весом Q=200 H прикреплена к стене шарниром А и опирается на опору С (рис. 1.17, а). К ее концу В шарнирно прикреплен брус ВК весом Р=400Н, опирающийся на выступ D. При этом СВ=АВ/3,

DK=BK/3, угол α=45°. Определить реакции опор, считая балку и брус однородными.

Рис. 1.17. К задаче 1.5.

Решение.

Расчленяя систему на две части, рассматриваем равновесие бруса ВК и балки АВ в отдельности. На брус ВК, (рис. 1.17, б) действуют сила 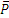и реакции связей 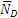, , 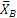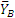. Вводя обозначение ВК=а и составляя для этих сил условия равновесия, получим:

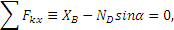
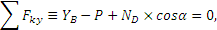
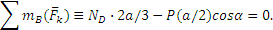
Решая эти уравнения, найдем:

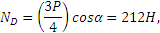
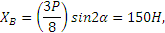
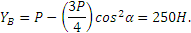
На балку АВ, если ее рассматривать отдельно, действуют сила 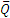, реакции внешних связей 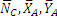и силы давления 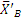и 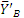бруса ВК, передаваемые через шарнир В (рис. 1.17, в). При этом по закону о действии и противодействии силы 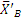и 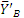должны быть направлены противоположно 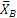и 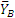; по модулю же Х’_B=Х_B, Y’_B=Y_B.

Вводя обозначение АВ=b и составляя для сил, действующих на балку, условия равновесия , получим:

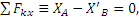
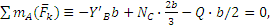
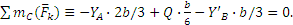
Полагая в этих уравнениях Х’_B=Х_B и Y’_B=Y_B и решая их, найдем:

X_A=X_B=150H, Y_A=Q/4-Y_B/2=-75H, NC=3Q/4+3YB/2=525H.

Из полученных результатов видно, что все реакции, кроме 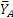, имеют направления, показанные на рис. 1.17, реакция же 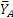фактически направлена вниз.

При решении задач этим путем важно иметь в виду, что если давление какого-нибудь одного тела на другое изображено силой 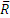или составляющим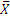и и 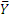, то на основании закона о действии и противодействии давление второго тела на первое должно изображаться силой 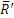, направленной противоположно 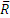(причем по модулю R'=R) или составляющими 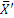, , 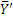направленными противоположно 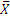и 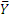(причем по модулю Х'=Х, Y'=Y).

Задача 1.6

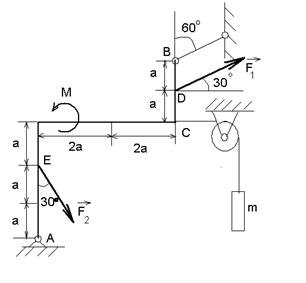
Жесткая рама, расположенная в вертикальной плоскости, закреплена в точке А шарнирно, а в точке В прикреплена к невесомому стержню с шарнирами на концах (рис.1.18 а). В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз массой 2,5 кг. На раму действует пара сил с моментом М=100 Нм и две силы F₁ =10 Н и F₂=40 Н, приложенные в точках D и Е. Определить реакции связей в точках А и В, вызываемые действующими нагрузками. При окончательных расчетах принять а=0,5 м, .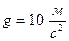

а)	б)
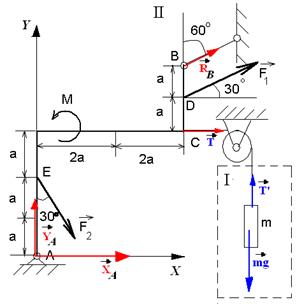
Рис.1.18. К задаче 1.6

Решение.

Освободим раму, груз и блок от связей, заменив их реакциями (рис.1.18.б). Реакцию связи неподвижного шарнира изобразим как две взаимно перпендикулярные силы 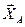и 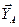(см.рис.1.2), сила реакции в точке B ( 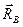) (направлена по невесомому стержню (см. рис. 1.4б), силы реакции гибкой нерастяжимой нити – вдоль нее ( 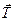и 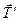) (см. рис.1.1). Добавим силу тяжести, действующую на груз. Разобьем рассматриваемую систему тел на две части: груз (I) и жесткая рама (II) .

Часть I

Уравнение равновесия в проекции на ось Y.

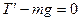, поэтому 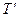= 25 Н.

Если рассмотреть условие равновесия блока (правило моментов), можно показать, что .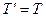

Часть II

Сумма проекций на ось X

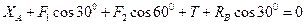
Сумма проекций на ось Y

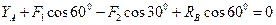
Если сила пересекает центр (например 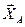и 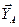), то ее момент относительно этого центра равен нулю. Поэтому оптимально составлять уравнения моментов относительно точки, в которой пересекается наибольшее число неизвестных сил.

Сумма моментов сил относительно точки A.

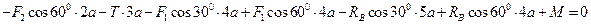
Из полученных уравнений имеем:

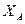= -80 Н , 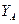= 14,5 Н и R_B = 30,2 Н.

Применив теорему Пифагора, получим R_А = 81,3 Н

Задача 1.7

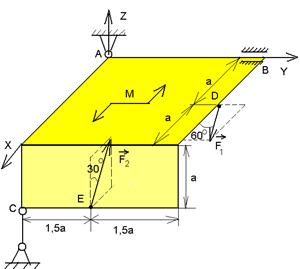
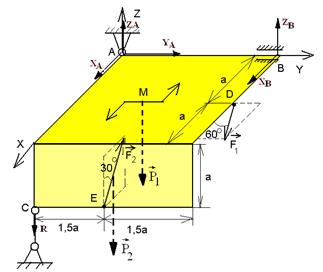
Две однородные прямоугольные плиты жестко соединены (сварены) под прямым углом друг к другу и закреплены сферическим шарниром в точке А, цилиндрическим шарниром в точке В и невесомым стержнем в точке С (рис.1.19.а). Размеры плит указаны на рисунке. Масса большей плиты 500 кг, меньшей 300 кг. На плиты действуют пары сил с моментом 4 кНм в плоскости XOY и две силы. Сила F₁ лежит в плоскости XOY и равна 6 кН, Сила F₂ лежит в плоскости XOZ и равна 8 кН.

Определить реакции связей в точках А и В и реакцию стержня. При подсчетах принять а=0,6 м.

а)	б)
Рис.1.19. К задаче 1.7.

Применим теорему освобождения от связей, и заменим их реакциями (рис.1.19 б). Запишем условия равновесия

Уравнение равновесия представляют собой систему из шести уравнений

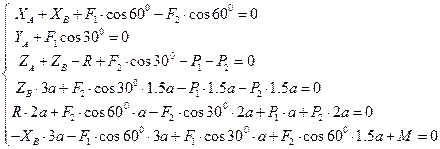
Решение системы приводит к следующему результату

X_A = -2 кН, Y_A = -5,2 кН, Z_A = 0, X_B = 3 кН, Z_B = 0,5 кН, R = -0,5 кН.

Кинематика

Кинематика точки

Определить движение точки - это значит определить ее положение по отношению к выбранной системе отсчета в любой момент времени. Для решения этой задачи в кинематике применяются три способа задания движения точки: векторный, координатный и естественный.

При векторном описания движения точки М ее радиус-вектор определяется как векторная функция от времени, т. е. 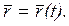(рис.2. 1а). Скорость 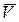точки, характеризующая быстроту и направление движения точки, равна производной по времени от ее радиуса-вектора: 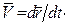Ускорение 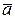точки, характеризующее изменение скорости по модулю и направлению, равно производной по времени от вектора скорости: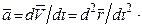

а)	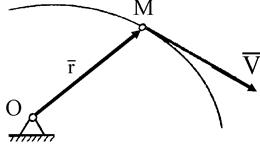б)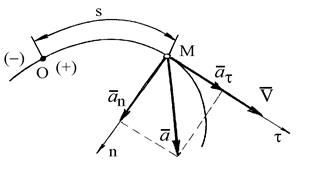
Рис. 2.1. Векторный (а) и естественный (б) способы определения движения точки.

Координатный способ определения (задания) движения точки состоит в том, что ее координаты в выбранной системе координат выражаются как функции времени t. Уравнения движения точки в декартовых координатах имеют вид: x = x(t), y = y (t), z = z (t). Если точка движется в плоскости Оху, то для ее описания достаточно только двух уравнений движения: x = x(t), y = y (t).

Для того чтобы найти траекторию точки, необходимо из уравнений движения исключить время t. Векторы скорости и ускорения определяются по их проекциям на оси декартовых координат следующими соотношениями:

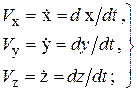
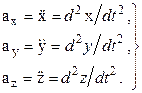(2.1)

Отсюда получаем формулы разложения векторов скорости 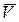и ускорения 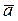по координатным осям: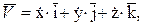 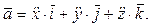Модули векторов скорости и ускорения вычисляем по формулам: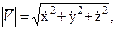

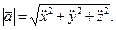
При естественном способе движение точки задается ее траекторией и уравнением движения по этой траектории: 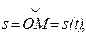где точка О - начало отсчета дуг на траектории; s - дуговая координата точки М или взятая с соответствующим знаком длина дуги, отсчитываемая вдоль траектории от начала отсчета до точки М (рис. 2.1 б). 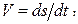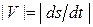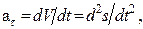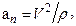Если заданы траектория точки и закон ее движения по этой траектории s = s(t), то вектор скорости направлен по касательной к этой траектории, а его проекция на направление касательной определяется по формуле причем абсолютное значение этой проекции равно модулю скорости: .Вектор ускорения определяется по его проекциям на естественные оси (касательную, главную нормаль и бинормаль): 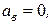где r - радиус кривизны траектории в данной точке. Следовательно, 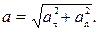Отметим важные частные случаи:

1. Если точка движется прямолинейно и неравномерно, то радиус кривизны траектории r ® µ и, следовательно, а_n = 0. В этом случае ускорение направлено вдоль траектории точки и по модулю равно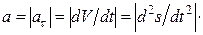

2. Если точка движется по криволинейной траектории равномерно, то V = const, и 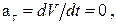и поэтому ускорение направлено по нормали к траектории и по модулю равно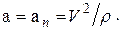

3. Если точка движется прямолинейно и равномерно, то a_n = 0, a_t = 0 и a = 0.

В том случае, когда движение точки задано в координатной форме, касательное ускорение определяется по формуле 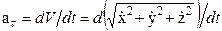, или 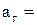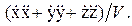После этого нормальное ускорение можно найти из равенства 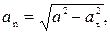где 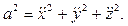Определив 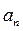, найдем радиус кривизны по формуле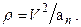

Если плоская траектория задана уравнением у = у(х), то радиус кривизны

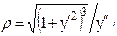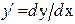траектории вычисляется по формуле: где и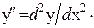

Вопросы для самоконтроля

1. Что называется траекторией точки?

2. Опишите способы задания движения.

3. Как при координатном способе задания движения точки определяется ее траектория?

4. Как найти проекции векторов скорости и ускорения точки на оси декартовой системы координат?

5. Как вычислить модули векторов скорости и ускорения точки по их проекциям на координатные оси?

6. Как определяются и что характеризуют нормальное и касательное ускорения точки?

7. Как найти радиус кривизны траектории в какой-либо ее точке?