Статика твердого тела

Предмет статики. Основные понятия статики: абсолютно твердое тело, сила, эквивалентная система сил, равнодействующая, уравновешенная система сил, силы внешние и внутренние. Аксиомы статики. Связи и реакции связей. Основные виды связей и их реакции: гладкая плоскость (поверхность и опора), гибкая нить, цилиндрический шарнир (подшипник), сферический шарнир (под-

пятник), невесомый (идеальный) стержень.

Система сходящихся сил. Геометрический и аналитический способы сложения сил. Сходящиеся силы, равнодействующая, геометрическое условие их равновесия. Аналитические условия равновесия для пространственной и плоской систем сходящихся сил. Теорема о равновесии трех непараллельных сил.

Теория пар сил. Момент силы относительно точки (центра) как вектор. Алгебраическое значение момента силы относительно точки. Момент пары сил как вектор и его алгебраическое значение. Теоремы об эквивалентности пар. Сложение пар сил в плоскости и произвольно расположенных в пространстве. Условия равновесия системы пар.

Плоская система сил. Теорема о параллельном переносе силы. Основная теорема статики о приведении плоской системы сил к данному центру. Главный вектор и главный момент системы сил и их расчет. Частные случаи приведения: приведение систем сил к паре сил, к равнодействующей. Аналитические условия равновесия для плоской системы сил: а) равенство нулю сумм проекций сил на две координатные оси и суммы их моментов относительно любого центра; б) равенство нулю сумм моментов сил относительно двух центров и суммы их проекций на одну ось; в) равенство нулю сумм моментов сил относительно трех центров. Условия равновесия системы параллельных сил. Теорема Вариньона о моменте равнодействующей.

Сосредоточенные и распределенные силы. Силы, распределенные по отрезку прямой, и их равнодействующая. Реакция жесткой заделки. Равновесие системы тел. Статически определимые и неопределимые системы. Равновесие при наличии сил трения. Коэффициент трения. Предельная сила трения. Угол и конус трения. Условие самоторможения. Трение качения, коэффициент трения качения и момент трения качения.

Пространственная система сил. Момент силы относительно оси и его расчет. Зависимость между моментом силы относительно центра и относительно оси, проходящей через этот центр. Аналитические формулы для вычисления моментов силы относительно координатных осей. Приведение пространственной системы сил к данному центру. Вычисление главного вектора и главного момента для пространственной системы сил. Аналитические условия равновесия произвольной пространственной системы сил.

Центр тяжести. Центр параллельных сил. Формулы для определения координат центра параллельных сил. Способы и формулы для определения положения (координат) центра тяжести объема, площади и линии его. Центры тяжести дуги окружности, треугольника и кругового сектора.

Кинематика

Кинематика точки. Предмет и задачи кинематики. Пространство и время в классической механике. Относительность механического движения.

Системы отсчета.Векторный способ задания движения точки. Траектория точки. Скорость точки как производная ее радиуса-вектора по времени. Ускорение точки как производная от ее вектора скорости по времени.

Координатный способ задания движения точки в прямоугольных декартовых координатах. Определение траектории точки. Определение скорости и ускорения точки по их проекциям на координатные оси.

Естественный способ задания движения точки. Естественный трехгранник и его оси. Алгебраическая величина скорости точки. Определение ускорения точки по его проекциям на оси естественного трехгранника; касательное и нормальное ускорения точки. Выражение касательного ускорения точки через проекции скорости и ускорения на координатные оси.

Поступательное движение твердого тела. Определение поступательного движения твердого тела. Теорема о траекториях, скоростях и ускорениях точек твердого тела при поступательном движении.

Вращательное движение твердого тела вокруг неподвижной оси. Определение вращательного движения тела вокруг неподвижной оси. Уравнение (закон) вращательного движения твердого тела. Угловая скорость и ускорение твердого тела. Законы равномерного и равнопеременного вращения. Скорость и ускорение точки тела, вращающегося вокруг неподвижной оси. Векторы угловой скорости и ускорения тела. Выражение скорости точки вращающегося тела и ее касательного и нормального ускорений в виде векторных произведений.

Плоскопараллельное (плоское) движение твердого тела. Плоское движение твердого тела и движение плоской фигуры в его плоскости. Разложение движения плоской фигуры на поступательное вместе с полюсом и вращательное вокруг полюса. Независимость угловой скорости и ускорения от выбора полюса. Теорема о скоростях точек и их проекциях для плоской фигуры. Мгновенный центр скоростей (МЦС) и доказательство его существования. Определение скоростей точек плоской фигуры с помощью МЦС. Теорема об ускорениях точек тела при плоском движении. Мгновенный центр ускорений (МЦУ).

Вращательное движение твердого тела вокруг неподвижной точки (сферическое движение). Углы Эйлера. Уравнения движения твердого тела вокруг неподвижной точки. Мгновенная ось вращения тела. Определение скорости и ускорения любой точки тела при его сферическом движении.

Свободное движение твердого тела. Уравнения движения для свободного твердого тела. Разложение свободного движения на поступательное движение вместе с полюсом и вращение вокруг полюса. Определение скоростей и ускорений точек свободного твердого тела.

Составное (сложное) движение точки. Переносное, относительное и абсолютное движения точки. Теорема Кориолиса о сложении скоростей и ускорений. Модуль и направление кориолисова ускорения (правило Н. Е. Жуковского). Случаи равенства нулю ускорения Кориолиса.

Составное движение твердого тела. Сложение поступательных движений. Сложение вращательных движений твердого тела вокруг параллельных и пересекающихся осей. Пара мгновенных вращений. Кинематический винт. Мгновенная винтовая ось.

Динамика

Основные законы динамики. Прямая и обратная задачи динамики. Уравнения движения механической системы. Закон изменения и сохранения импульса. Момент импульса, его изменение и сохранение. Кинетическая энергия, работа. Теорема об изменении кинетической энергии. Динамика поступательного и вращательного движения твердого тела и плоского движения. Теория удара

а

а.

Статика

Основные положения

Статикой называется раздел теоретической механики, в котором изучаются операции с силами и состояние равновесия тел под действием на них сил не только в состоянии покоя, но и при движение их по инерции. В основе статики лежат экспериментально установленные аксиомы (законы).

1. Аксиома инерции. Под действием взаимно уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется прямолинейно и равномерно.

2. Аксиома равновесия двух сил. Две силы, приложенные к абсолютно твердому телу, будут уравновешены тогда и только тогда, когда они равны по модулю, действуют по одной прямой и направлены в противоположные стороны.

3. Аксиома присоединения и исключения уравновешивающихся сил. Действие системы сил на абс. твердое тело не изменится, если к ней прибавить или отнять уравновешенную систему сил. Следствие: Действие силы на абс.тв. тело не изменится, если перенести точку приложения силы вдоль ее линии действия.

4. Аксиома параллелограмма сил. Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах.

5. Аксиома равенства действия и противодействия (3-й закон Ньютона). Всякому действию соответствует равное и противоположно направленное противодействие.

6. Принцип отвердевания. Равновесие сил, приложенных к нетвердому телу, не нарушается при его затвердевании.

Равновесие свободных тел может быть нарушено при действии на них сил. Тела или системы тел считаются несвободными, если их перемещению препятствуют другие тела (связи), скрепленные или соприкасающиеся с ними. Сила, с которой данная связь действует на тело, препятствуя его перемещению, называется силой реакции связи или просто реакцией связи. Значения реакций связей определяются в процессе решения соответствующей задачи механики. Реакция связи направлена в сторону, противоположную той, куда она не дает перемеща-ться телу. На рис.1.1. представлены наиболее часто встречающиеся типы связей и их направления: в случае гладкой плоскости (поверхности) или опоры, для которых реакция 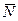направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке. Связь, осуществленная в виде гибкой нерастяжимой нити (каната, цепи, ремня и пр.), не дает телу М удаляться от точки ее подвеса А по направлению АМ (рис. 1.1 г). Поэтому реакция 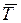натянутой нити направлена вдоль нее от тела к точке подвеса.

Цилиндрическим шарниром или подшипником (шарнирно-неподвижной опорой) называется совокупность неподвижной обоймы (втулки) 1 и помещенного в нее валика (пальца) 2, жестко соединенного с телом 3 (рис.1. 2а). В точке С соприкосновения втулки с валиком возникает сила опорной реакции, прохо-

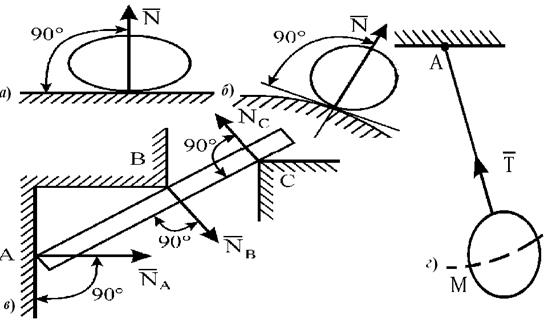
Рис. 1.1. Примеры наиболее часто встречающихся типов связей: в случае гладкой плоскости (а, б), опоры (в), гибкой нерастяжимой нити (г).

дящая через геометрический центр А валика и направленная по нормали к идеально гладким поверхностям. Так как положение точки С соприкосновения валика со втулкой заранее не известно, то невозможно сразу указать направление силы реакции 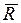, но можно утверждать, что линия действия реакции 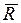всегда пройдет через центр А шарнира. На расчетных схемах для шарнирно-неподвижной опоры (рис. 1.2б) при решении задач неизвестную по модулю и направлению реакцию 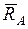представляют в виде двух ее взаимно перпендикулярных составляющих 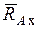и . После определения их значений находят значение реакции 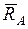и ее направление по формулам: , .

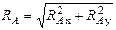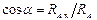а)	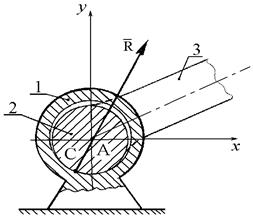б)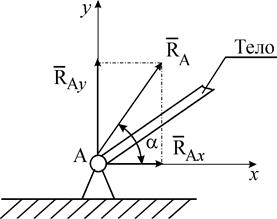
Рис. 1.2. - Цилиндрический шарнир/подшипник (шарнирно-неподвижная опора) (а) и ее расчетная схема (б).

Реакция связи 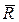шарнирно-подвижной опоры (опоры на катках) проходит

через ее центр (рис. 1.3а и б) и перпендикулярно к опорной плоскости. Сферическим шарниром называется устройство, выполненное в виде двух контактирующих сфер, геометрический центр А которых неподвижен (рис. 1.3в). Тело 3 в равновесии жестко связано с внутренней подвижной сферой 1. Для гладкой сферической поверхности реакция 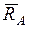направлена по нормали к этим поверхностям и проходит через центр А сферы. На расчетных схемах реакцию 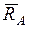представляют в виде трех ее взаимно перпендикулярных составляющих 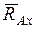, 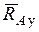и 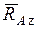, направленных вдоль координатных осей.

а)	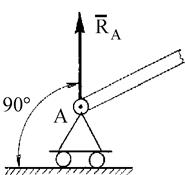б)	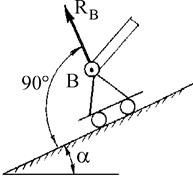в)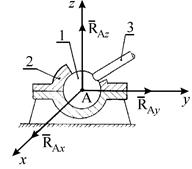
Рис. 1.3 Шарнирно-подвижная опора (а), опора на катках (б), сферический шарнир (в).

Подпятник представляет собой соединение цилиндрического шарнира 2 и опорной плоскости 3, на которую опирается вал 1(рис. 1.4а). Реакция подшипника, лежащая в плоскости перпендикулярной оси вала, представляется двумя ее взаимно перпендикулярными составляющим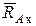и и 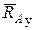, а реакция опорной плоскости - реакцией 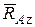, направленной по нормали к этой плоскости.

Реакция 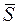прямолинейного невесомого (идеального) стержня направлена вдоль него (рис. 1.4 б). Если связью является криволинейный стержень, то реакция направлена вдоль прямой АВ, соединяющей концевые шарниры А и В (рис. 1.4 в).

а)	б)	в)
Рис. 1.4. Подпятник (а), невесомые прямолинейный (б) и криволинейный (в) стержни.

Жесткая заделка (неподвижное защемление) конца балки не допускает не только линейных перемещений балки 1 вдоль координатных осей, но и вращения балки в плоскости хАу (рис. 1.5). Нахождение реакций жесткой заделки сводится к определению трех неизвестных величин: составляющих 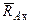и 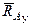реакции 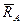и так называемого реактивного момента М_А, препятствующего вращению балки в плоскости хАу вокруг точки А.

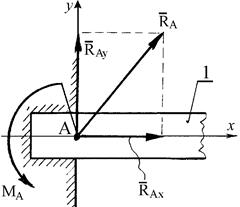
Рис. 1.5. Жесткая заделка (неподвижное защемление).

Для составления уравнений равновесия в статике необходимо уметь вычислять проекции сил на координатные оси и выполнять операции сложения и разложения сил. Проекцией силы на ось называется алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси. Так, для сил, изображенных на рис. 1.6а и б:

F_x =a₁b₁=Fcos a;

F_у = a₂b₂= Fcos (90°- a) =F sin a;

Q_x= c₁d₁=Qcosb=Q cos (180°+ g) = - Q cosg;

Q_у = c₂d₂= Qcos (90°+g) = - Qsin g.

Проекцией силы 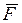на плоскость Оху называется вектор 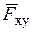= 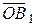, заключенный между проекциями начала и конца силы 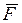на эту плоскость (рис. 1.6в). По модулю F_ху = F cos q, где q - угол между направлением силы 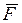и ее проекцией 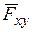. В некоторых случаях для нахождения проекции силы на ось удобнее сначала найти ее проекцию на плоскость, в которой расположена эта ось, а затем полученный вектор спроецировать на данную ось. Например, на рис. 1.6в F_х =ОВ₂= F_ху cos j = Fcos q × cosj,

F_у = ОВ₃ = F_ху sin j = F cos q ×sin j.

а)	б)	в)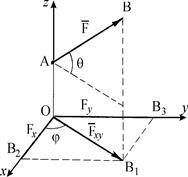
Рис. 1.6. Проекции сил на оси координат (а и б) и плоскость (в).

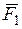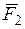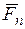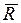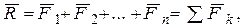
Геометрический метод сложения сил , , ..., основан на построении в масштабе векторного (силового) многоугольника, замыкающая сторона которого представляет эту сумму и называется главным вектором : 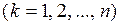(рис. 1.7а).

а) 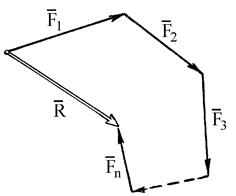б)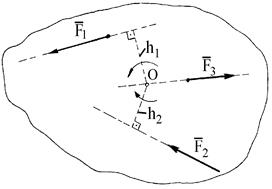

Рис. 1.7. Геометрический метод сложения сил (а). Определение момента силы относительно точки О на плоскости (б).

Аналитический метод сложения сил основан на известной теореме векторной алгебры: проекция вектора суммы на ось равна алгебраической сумме проекций слагаемых векторов на ту же ось: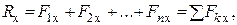

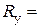
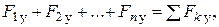
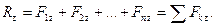Модуль (численное

значение) главного вектора равен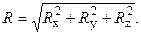

Действие силы на твердое тело может вызвать вращательный эффект, который для плоской системы сил можно оценить с помощью момента силы относительно какой-либо точки О на плоскости: 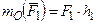; 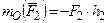(рис. 7б), где h₁ и h₂ - плечи сил 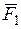и 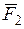относительно точки О. Плечом называется длина перпендикуляра, опущенного из точки О на линию действия соответствующей силы. Если данная сила стремится вращать тело вокруг точки О против хода часовой стрелки, то ее моменту относительно этой точки приписывают знак “+”. Момент силы относительно точки равен нулю, если линия действия силы проходит через эту точку, так как при этом плечо равно нулю (например, ).

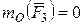Вычисление момента силы относительно какой-либо точки во многих случаях упрощается, если эту силу разложить на две взаимно перпендикулярные составляющие и применить теорему Вариньона, согласно которой момент равнодействующей сходящихся сил относительно любого центра равен сумме моментов составляющих сил относительно того же центра. Например, для равнодействующей силы 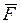и ее составляющих 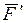и 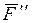(рис. 1.8а) имеем: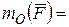 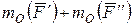, где 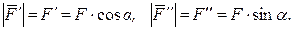Таким образом,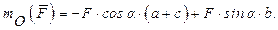

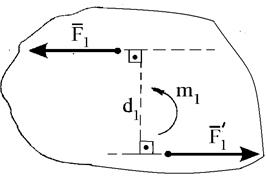
Вращательный эффект вызывает также пара сил - совокупность двух сил, равных по модулю, направленных в противоположные стороны и линии действия которых параллельны (рис. 1.8б). Пара сил, стремящаяся вращать тело против хода часовой стрелки, считается положительной, а по ходу часовой стрелки - отрицательной. Пара сил характеризуется ее моментом m, который равен взятому со знаком “плюс” или “минус” произведению модуля одной из сил данной

пары на плечо пары, т. е. на кратчайшее расстояние между линиями действия сил пары (d ). Моменты сил на рис. 1.8б равны: m₁ = F₁×d₁; m₂ = -F₂×d₂. Систему пар сил, расположенных в одной плоскости, можно заменить одной эквивалентной парой, момент которой М равен алгебраической сумме моментов пар:

М = m₁ + m₂ + ... + m_n = 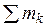(k = 1, 2, ..., n).

а)	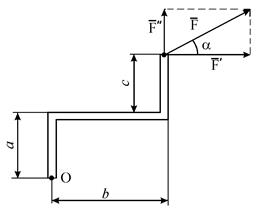б)
Рис. 1.8. Иллюстрация теоремы Вариньона (а). Пара сил (б).