Произвольная пространственная система сил

Моментом силы 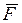относительно центра О называется приложенный в этом центре вектор 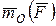, модуль которого равен произведению модуля силы 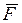на ее плечо h. Момент силы направлен перпендикулярно плоскости, проходящей через центр О и линию действия силы в ту сторону, откуда “вращение”, совершаемое силой вокруг точки О, представляется происходящим против хода часовой стрелки (рис. 9):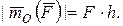

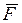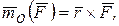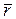Момент силы относительно центра О может быть представлен в виде векторного произведения: где - радиус-вектор точки приложения силы, так как модуль векторного произведения равен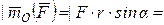

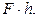Вектор 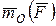направлен перпендикулярно плоскости, проходящей через векторы 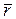и 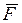, в ту сторону, откуда кратчайший поворот вектора 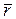к направлению вектора 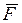представляется происходящим против хода часовой стрелки.

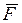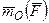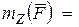
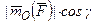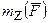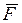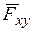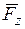Моментом силы относительно оси z, проходящей через центр О, называется скалярная величина, равная проекции вектора на эту ось: . Механический смысл величины состоит в том, что она характеризует вращательный эффект силы, когда эта сила стремится повернуть тело вокруг оси z. В самом деле, если разложить силу на составляющие и , где 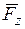úú Oz (рис. 10 а), то поворот вокруг оси z будет совершать только составляющая 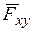и вращательный эффект всей силы 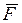будет определяться величиной 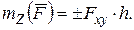Составляющая же 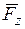повернуть тело вокруг оси z не может, она лишь может сдвинуть тело вдоль оси z.

Рис. 1.9. Определение момента силы 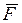относительно центра О.

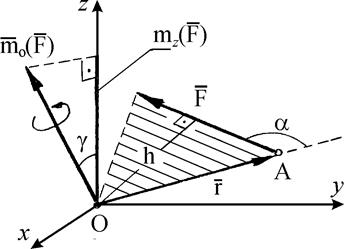
Момент силы относительно оси z будет иметь знак “плюс”, когда с положительного конца этой оси поворот, который стремится совершить сила 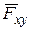вокруг этой оси, виден происходящим против хода часовой стрелки, и знак “минус” - когда по ходу часовой стрелки. Для расчета момента какой-либо силы 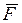относительно какой-либо оси z (рис. 1.10б) нужно провести любую плоскость (ху), перпендикулярную к данной оси и, спроектировав силу на эту плоскость, найти алгебраическую величину момента полученной проекции 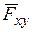относительно точки О пересечения оси z с плоскостью ху по формуле: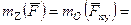 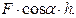. Поэтому момент силы относительно оси равен нулю, когда угол 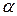=0, т.е. сила параллельна оси z или, когда линия действия силы пересекает эту ось.

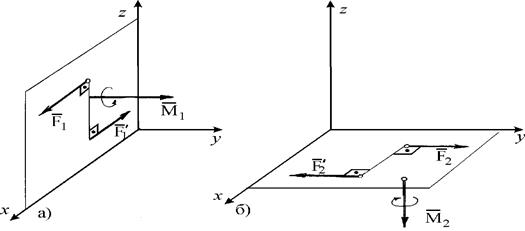
При изучении равновесия произвольной пространственной системы сил приходится определять моменты пар сил относительно осей в виде вектора, направленного по перпендикуляру к плоскости действия пары в ту сторону, откуда вращение тела этой парой сил представляется происходящим против направления вращения часовой стрелки. Изображенные на рис.1.11, а и б векторы 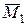и 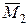представляют собой соответственно моменты пар сил 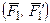и .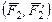

Так как пару сил можно переносить в ее плоскости действия и в любую другую плоскость, ей параллельную, то ее момент 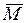не имеет определенной точки приложения и является свободным вектором, который можно переносить параллельно самим себе в любую точку тела.

а)	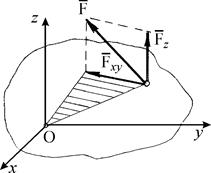б)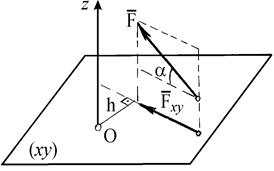
Рис. 1.10. Определение момента силы относительно оси z, проходящей через центр О (а) и схема его расчета (б).

При определении момента пары сил относительно какой-либо оси достаточно найти его проекцию этого вектора этой пары на данную ось, например, на рис. 1.11а и б, величины М_1х = М_1z = 0; М_1у = М₁; М_2х = М_2у = 0; М_2z = - M₂.

Рис. 1.11. Определение момента пары сил как вектора.

Для сложения пар сил достаточно перенести их моменты как свободные векторы (параллельно самим себе) в общую точку и применить правило сложения векторов. Так, на примере двух пар сил 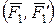и 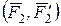, расположенных в плоскостях xBy и xBz соответственно (рис. 1.12),выполняется соотношение: 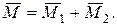Модуль М результирующего вектора 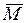находится как величина диагонали прямоугольника, построенного на векторах 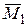и 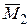: 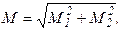или в проекциях на координатные оси: M_x = M_1x + M_2x = 0; M_y = M_1y + M_2y =- M₂;

M_z = M_1z + M_2z = M₁, следовательно,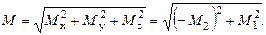

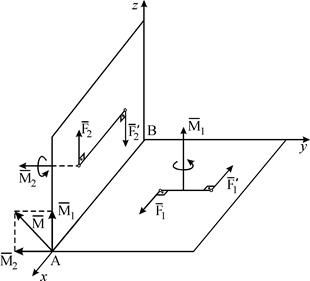
Рис. 1.12. Сложение моментов пар сил.

Любую пространственную систему сил можно привести к некоторому центру О с главным вектором 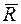, приложенным в этом центре, и главным моментом 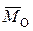относительно этого центра. Главный вектор равен геометрической сумме всех сил: 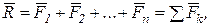и не зависит от выбора центра приведения, а главный момент 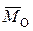равен геометрической сумме векторов-моментов всех сил относительно этого центра (включая и векторы-моменты всех пар сил) и зависит от выбора центра приведения: .

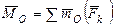Условиями равновесия произвольной пространственной системы сил являются равенство нулю главного вектора и главного момента этой системы сил относительно любого центра, что выражается шестью уравнениями в проекциях на оси декартовой системы координат: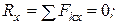

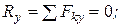
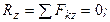
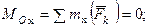
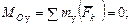
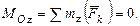
Вопросы для самоконтроля

1. Как определить момент силы относительно оси?

2. В каких случаях момент силы относительно оси равен нулю?

3. Как представить вектор-момент пары сил, расположенной в пространстве?

4. Как складываются пары сил в пространстве?

5. Как вычислить главный вектор и главный момент пространственной произвольной системы сил?

6. Каковы условия (уравнения) равновесия для произвольной пространственной системы сил?