Регрессионный анализ
Регрессионный анализ позволяет получить функциональную зависимость между некоторой случайной величиной Y и некоторыми влияющими на Y величинами X. Такая зависимость получила название уравнения регрессии. Различают простую (парную) и множественную регрессию линейного и нелинейного типа.
Пример простой линейной регрессии:
y=m1x+b.
Пример множественной линейной регрессии:
| y=m1x1+m2x2+... + mkxk+b. | (1) |
Для оценки степени связи между величинами используется коэффициент множественной корреляции R Пирсона (корреляционное отношение), который может принимать значения от 0 до 1. R=0 если между величинами нет никакой связи и R=1, если между величинами имеется функциональная (детерминированная) связь. В большинстве случаев R принимает промежуточные значения от 0 до 1. Величина R2 называется коэффициентом детерминации.
Задачей построения регрессионной зависимости является нахождение вектора коэффициентов M модели (1) при котором коэффициент R принимает максимальное значение.
Для оценки значимости R применяется F-критерий Фишера, вычисляемый по формуле
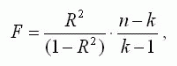
где n - размер выборки (количество экспериментов); k - число коэффициентов модели. Если F превышает некоторое критическое значение для данных n и k и принятой доверительной вероятности, то величина R считается существенной. Таблицы критических значений F приводятся в справочниках по математической статистике.
Таким образом, значимость R определяется не только его величиной, но и соотношением между количеством экспериментов и количеством коэффициентов (параметров) модели. Действительно, корреляционное отношение для n=2 для простой линейной модели равно 1 (через 2 точки на плоскости можно всегда провести единственную прямую). Однако, если экспериментальные данные являются случайными величинами, доверять такому значению R следует с большой осторожностью. Обычно для получения значимого R и достоверной регрессии стремятся к тому, чтобы количество экспериментов существенно превышало количество коэффициентов модели (n>>k).
Для построения линейной регрессионной модели необходимо:
1) подготовить список из n строк и m столбцов, содержащий экспериментальные данные (столбец, содержащий выходную величину y должен быть либо первым, либо последним в списке);
2) обратиться к меню Сервис/Анализ данных/Регрессия

Если пункт "Анализ данных" в меню "Сервис" отсутствует, то следует обратиться к пункту "Надстройки" того же меню и установить флажок "Пакет анализа".
3) в диалоговом окне "Регрессия" задать:
· входной интервал Y;
· входной интервал X;
· выходной интервал - верхняя левая ячейка интервала, в который будут помещаться результаты вычислений (рекомендуется разместить на новом рабочем листе);
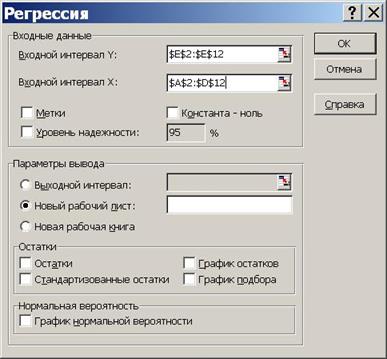
4) нажать "Ok" и проанализировать результаты.
Пример использования множественной линейной регрессии
Предположим, что застройщик оценивает стоимость группы небольших офисных зданий в традиционном деловом районе.
Застройщик может использовать множественный регрессионный анализ для оценки цены офисного здания в заданном районе на основе следующих переменных.
y - оценочная цена здания под офис;
x1 - общая площадь в квадратных метрах;
x2 - количество офисов;
x3 - количество входов (0,5 входа означает вход только для доставки корреспонденции);
x4 - время эксплуатации здания в годах.
В этом примере предполагается, что существует линейная зависимость между каждой независимой переменной (x1, x2, x3 и x4) и зависимой переменной (y), то есть ценой здания под офис в данном районе. Исходные данные показаны на рисунке.
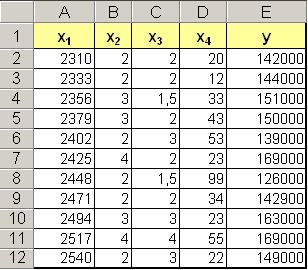
Настройки для решения поставленной задачи показаны на рисунке окна "Регрессия". Результаты расчетов размещены на отдельном листе в трех таблицах
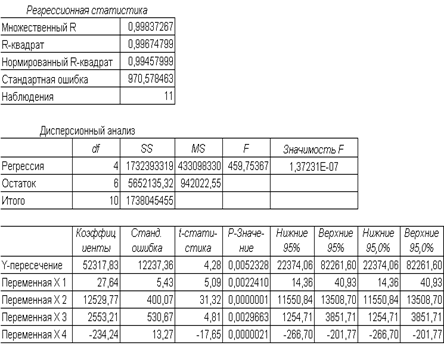
В итоге мы получили следующую математическую модель:
y = 52318 + 27,64*x1 + 12530*x2 + 2553*x3 - 234,24*x4.
Теперь застройщик может определить оценочную стоимость здания под офис в том же районе. Если это здание имеет площадь 2500 квадратных метров, три офиса, два входа и время эксплуатации - 25 лет, можно оценить его стоимость, используя следующую формулу:
y = 27,64*2500 + 12530*3 + 2553*2 - 234,24*25 + 52318 = 158 261 у.е.
В регрессионном анализе наиболее важными результатами являются:
· коэффициенты при переменных и Y-пересечение, являющиеся искомыми параметрами модели;
· множественный R, характеризующий точность модели для имеющихся исходных данных;
· F-критерий Фишера (в рассмотренном примере он значительно превосходит критическое значение, равное 4,06);
· t-статистика – величины, характеризующие степень значимости отдельных коэффициентов модели.
На t-статистике следует остановиться особо. Очень часто при построении регрессионной модели неизвестно, влияет тот или иной фактор x на y. Включение в модель факторов, которые не влияют на выходную величину, ухудшает качество модели. Вычисление t-статистики помогает обнаружить такие факторы. Приближенную оценку можно сделать так: если при n>>k величина t-статистики по абсолютному значению существенно больше трех, соответствующий коэффициент следует считать значимым, а фактор включить в модель, иначе исключить из модели. Таким образом, можно предложить технологию построения регрессионной модели, состоящую из двух этапов:
1) обработать пакетом "Регрессия" все имеющиеся данные, проанализировать значения t-статистики;
2) удалить из таблицы исходных данных столбцы с теми факторами, для которых коэффициенты незначимы и обработать пакетом "Регрессия" новую таблицу.
Для примера рассмотрим переменную x4. В справочнике по математической статистике t-критическое с (n-k-1)=6 степенями свободы и доверительной вероятностью 0,95 равно 1,94. Поскольку абсолютная величина t, равная 17,7 больше, чем 1,94, срок эксплуатации - это важная переменная для оценки стоимости здания под офис. Аналогичным образом можно протестировать все другие переменные на статистическую значимость. Ниже приводятся наблюдаемые t-значения для каждой из независимых переменных:
| Общая площадь | 5,1 |
| Количество офисов | 31,3 |
| Количество входов | 4,8 |
| Срок эксплуатации | 17,7 |
Все эти значения имеют абсолютную величину большую, чем 1,94; следовательно, все переменные, использованные в уравнении регрессии, полезны для предсказания оценочной стоимости здания под офис в данном районе.
Поиск решения
Excel имеет несколько программ-надстроек, выполняющих решение различных задач. Одной из надстроек является "Поиск решения", позволяющая решать оптимизационные задачи в Excel. Чаще всего это задачи линейного программирования (ЛП).
Общая формулировка задачи ЛП: найти неотрицательное решение X системы линейных уравнений AX=B, при котором целевая функция f=CX принимает максимальное (минимальное) значение, где A — матрица коэффициентов; B — объемы ресурсов.
Экономический смысл системы AX=B заключается в задании ограничений на расходуемые ресурсы.
Экономический смысл целевой функции f=CX заключается в максимальной прибыли или минимальной себестоимости, получаемой от оптимального решения X. Например, если X — вектор объемов выпуска продукции, а С - вектор прибыли, получаемой от единицы каждого вида продукции, то f — суммарная прибыль от выпуска всей продукции.
Рассмотрим работу надстройки "Поиск решения" на примере задачи о рационе кормления животных. Требуется составить такой рацион кормления животных тремя видами корма, при котором они получат необходимое количество питательных веществ A и B и себестоимость кормов будет минимальна. Цены кормов, требуемое количество питательных веществ и их содержание в каждом корме показаны в таблице.
| Питательные вещества | Корм 1 | Корм 2 | Корм 3 | Требуемое количество (ед. пит. вещества) |
| А (ед./кг) | ||||
| Б (ед./кг) | ||||
| Цена корма (руб/кг) | 2,20 | 1,95 | 2,87 |
Если обозначить X=(x1, x2, x3) — искомое количество кормов, то задача ЛП формулируется так:
Найти решение X системы
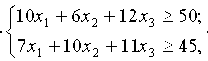
при котором целевая функция

принимает минимальное значение.
Математическую формулировку задачи необходимо оформить в виде таблицы, отражающей основные зависимости.
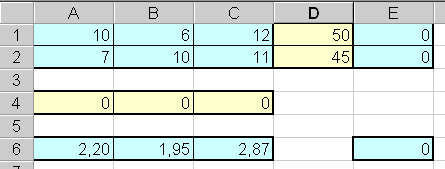
Ячейки таблицы имеют следующий смысл:
· диапазон A1:C2 — содержит матрицу A;
· диапазон D1:D2 — содержит вектор ресурсов В;
· диапазон A6:C6 — содержит вектор цен С;
· диапазон A4:C4 — содержит вектор решений X, начальные значения которого заданы нулю и который будет оптимизирован программой;
· диапазон E1:E2 — содержит выражения, вычисляющие произведение AX;
· ячейка E6 — содержит выражение, вычисляющее f=CX.
Вызов программы поиска решения выполняется через меню "Сервис\Поиск решения...". В открывшемся окне "Поиск решения" необходимо установить следующие параметры:
· "Установить целевую ячейку" — E6;
· установить переключатель "Равной минимальному значению";
· в поле "изменяя ячейки" указать диапазон A4:C4;
· в области "Ограничения" нажать кнопку "Добавить" и в окне "Добавление ограничений" ввести ограничения: E1>=D1 и E2>=D2;
· нажать кнопку "Параметры..." и в открывшемся окне установить флажки "Линейная модель", "Неотрицательные значения" и выбрать переключатель "Оценка" — "Линейная".
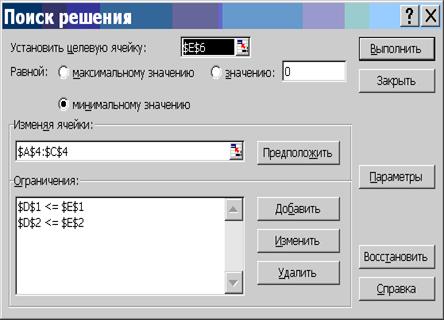
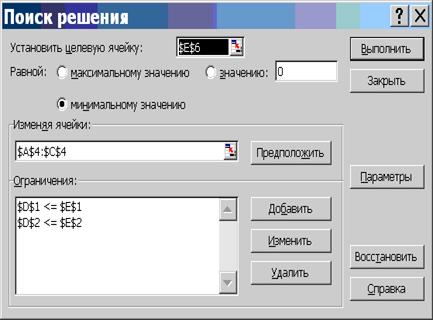
Для запуска программы необходимо в окне "Поиск решения" нажать кнопку "Выполнить". Результаты вычислений будут записаны в изменяемые ячейки таблицы. В итоге таблица должна иметь следующий вид.
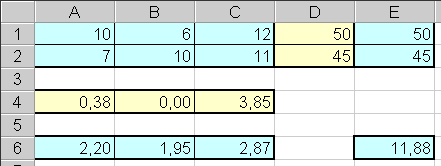
Таким образом, животных следует кормить первым кормом в количестве 0,38 кг, третьим — 3,85 кг и не использовать второй корм вообще. При таком рационе затраты на кормление одного животного составят 11,88 руб.
Работа с макросами
Макрос — это программа, автоматизирующая выполнение различных часто повторяющихся операций. Понятие макроса и управление его записью и применением аналогичны рассмотренным в текстовом процессоре Word.
Основной задачей пользователя является аккуратное выполнение требуемой последовательности операций в реальной таблице при включенном макрорекордере. Макрорекордер преобразует выполняемые действия в последовательность команд языка VBA.
Работая с книгой Excel, пользователь может записать несколько макросов. Все они сохраняются в VBA-модуле. Запуск макроса выполняется одним из трех способов:
с помощью "горячих" клавиш;
посредством выбора имени макроса в меню;
щелчком мыши по графическому объекту, связанному с макросом.
Дата добавления: 2015-12-08; просмотров: 1252;
