Методы представления колебаний
Существуют различные методы описания гармонических колебаний. Приведём некоторые из них.
1. Аналитический метод
Задаётся уравнение колебаний гармонического осциллятора
х=Аsin(ωt+φ0)
по которому и определяется смещение его от положения равновесия в любой момент времени.
2. Графический метод
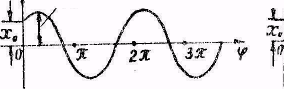
| Рис.5.3 |
3. Метод векторной диаграммы
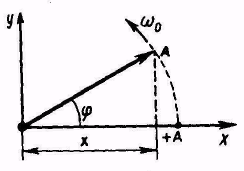
| Рис.5.4 |
x = Asin(ω0t+φ0), совершая гармоническое колебание.
§ 5.2.2 Скорость и ускорение колеблющейся точки
Чтобы найти скорость материальной точки при гармоническом колебании, возьмем производную от смещения колеблющейся точки x = Asin(ω0t+φ0) по времени:
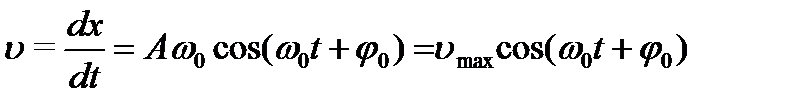 (5.4)
(5.4)
где υmax = Аω0 — максимальная скорость (амплитуда скорости).
На основании тригонометрических формул преобразуем (4.18):
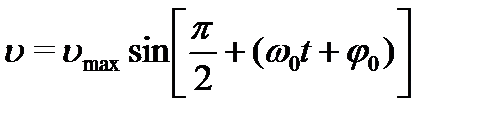 (5.5)
(5.5)
Сравнивая выражения для смещения и скорости замечаем, что фаза скорости на 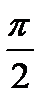 больше фазы смещения, т.е. скорость опережает по фазе смещение на
больше фазы смещения, т.е. скорость опережает по фазе смещение на 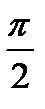 Продифференцировав (5.4), найдем ускорение:
Продифференцировав (5.4), найдем ускорение:
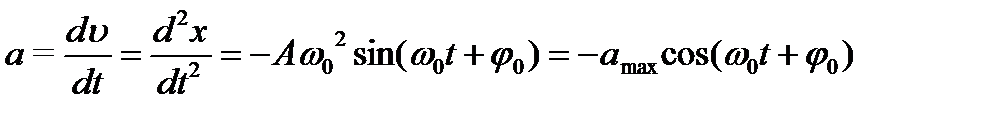 (5.6)
(5.6)
где аmax = А ω02 - максимальное ускорение (амплитуда ускорения).
Вместо (5.5) запишем
а = аmax соs [π + (ω0t+φ0)] (5.7)
Из сравнения (5.6) и (5.3) следует, что фазы ускорения и смещения различаются на π, т. е. эти величины изменяются в противофазе. Это значит, что при положительном максимальном смещении ускорение максимально, но отрицательно. На рисунке показаны графические зависимости смещения, скорости и ускорения от времени (рис.6.6, а) и их векторные диаграммы (рис.5.6, б) .
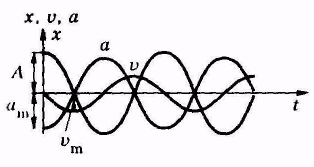
| Рис.5.6 |
| б ) |
| а ) |
§ 5.2.3 Кинетическая и потенциальная энергии колебательного движения
Колеблющееся тело обладает как кинетической, так и потенциальной энергией, которые последовательно переходят друг в друга при колебаниях осциллятора. Полная энергия осциллятора равна сумме кинетической и потенциальной энергии:
Е = Ек+Еп (5.8)
Кинетическая энергия тела, колеблющегося по гармоническому закону, вычисляют по формуле:
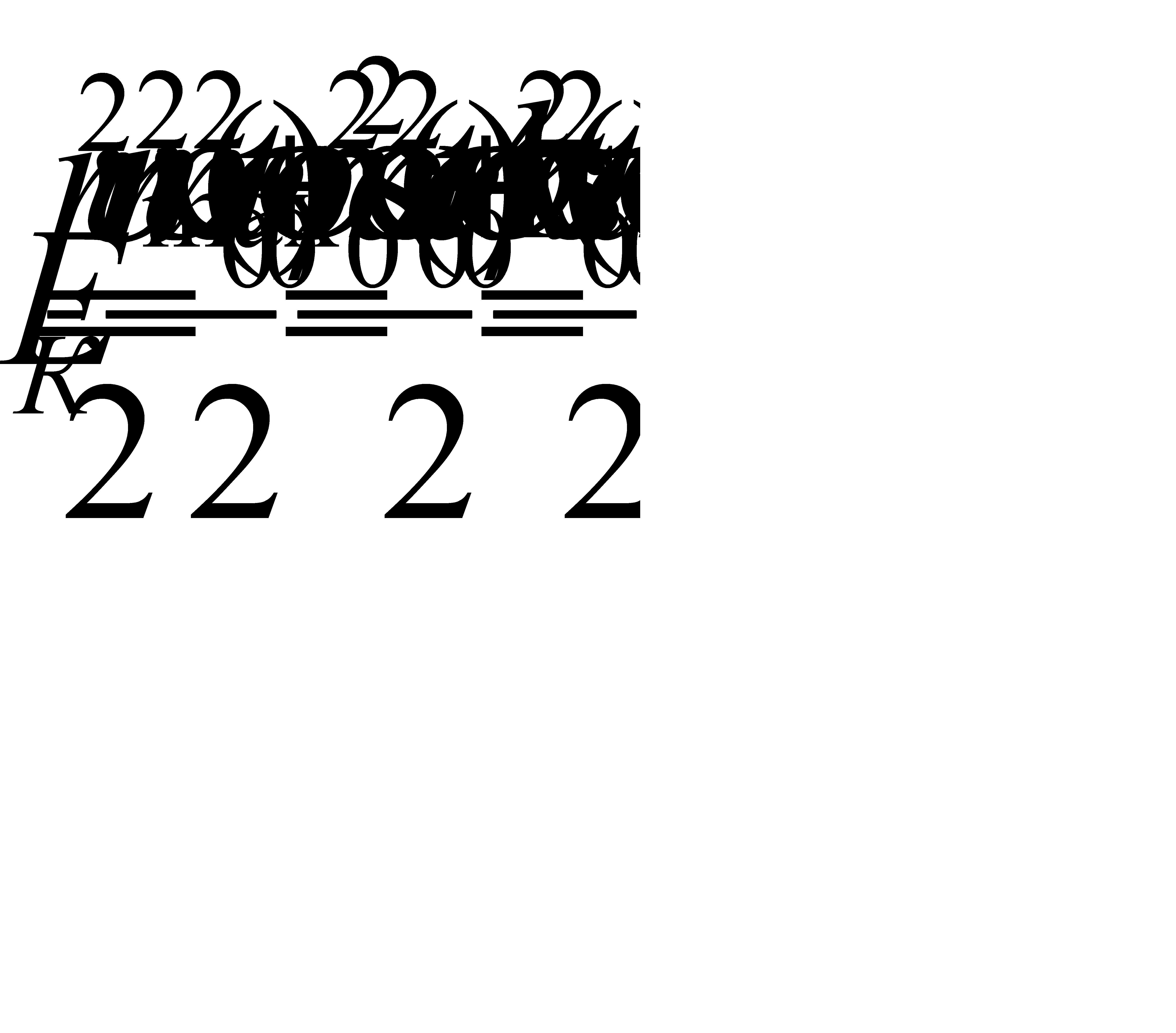 (5.9)
(5.9)
с учётом mω2 = k
Потенциальную энергию колебательного движения найдём, исходя из формулы для потенциальной энергии упругой деформации:
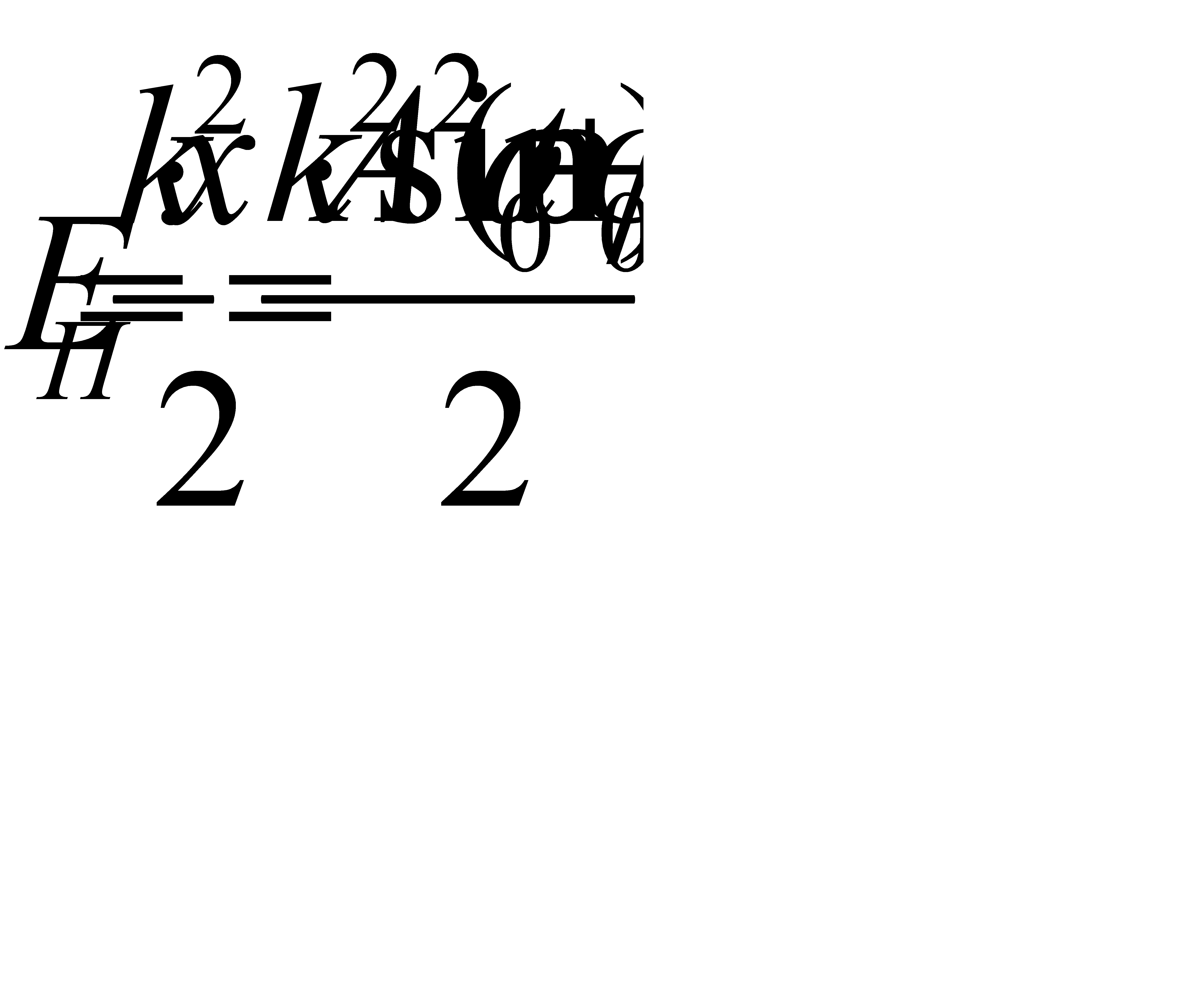 (5.10)
(5.10)
Складывая кинетическую и потенциальную энергию, получим полную механическую энергию материальной точки, колеблющейся по гармоническому закону:
 (5.11)
(5.11)
Полученное выражение показывает, что энергия колеблющегося тела от времени не зависит, т.е. с течением времени остаётся величиной постоянной, а зависит только от квадрата амплитуды и частоты.
При отсутствии сил трения полная механическая энергия системы не изменяется:
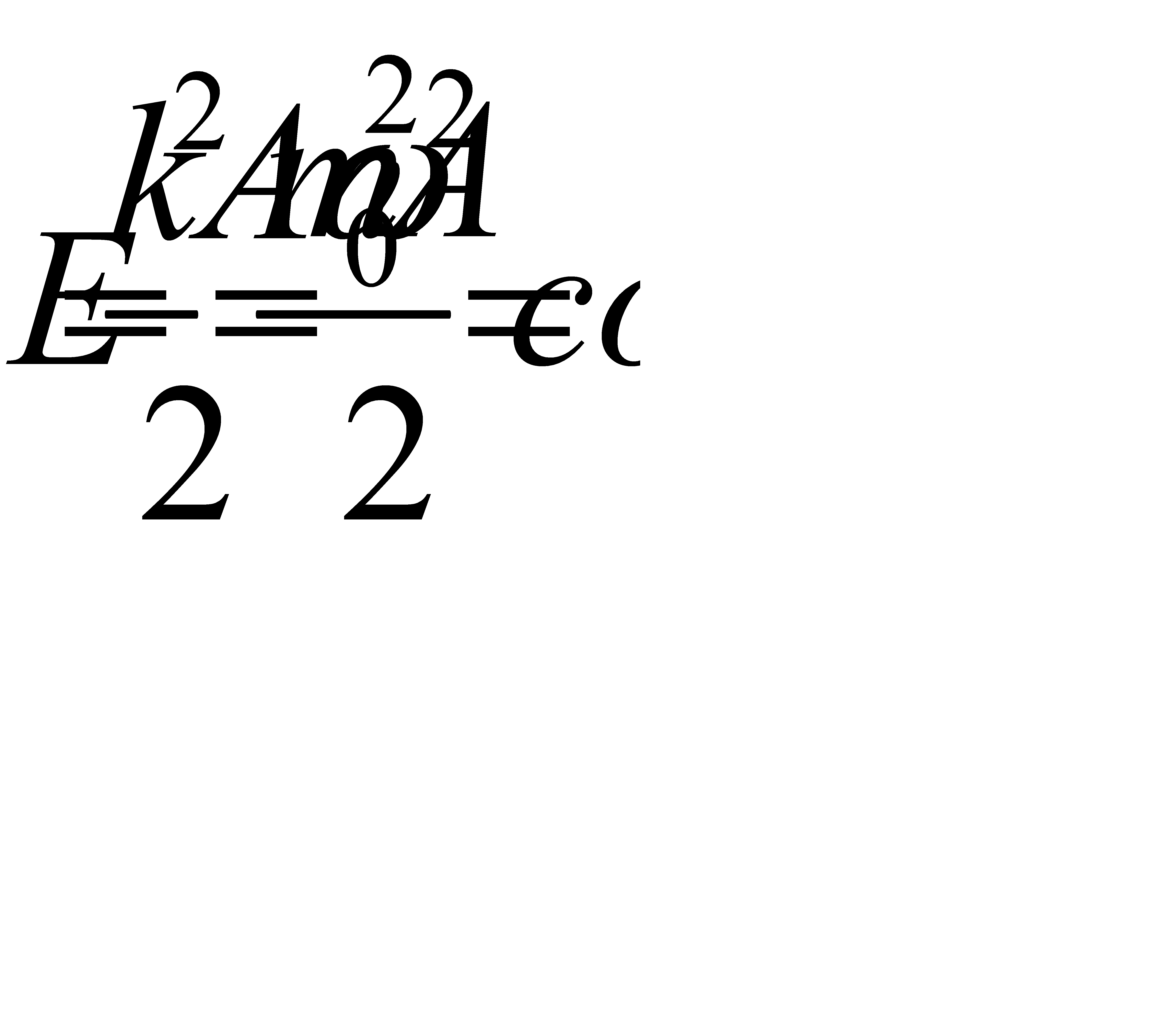 (5.12)
(5.12)
Графически зависимости кинетической, потенциальной и полной механической энергий колеблющейся системы от времени показаны на рис. 5.7, а.
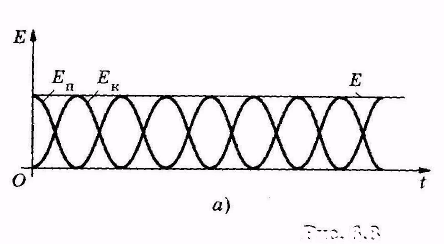
| Рис.5.7 |
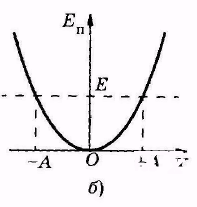
Потенциальная яма (ограниченная область пространства, в которой потенциальная энергия меньше, чем в не её), соответствующая гармоническому колебанию, изображена на рис. 5.7, б. Она определяется зависимостью 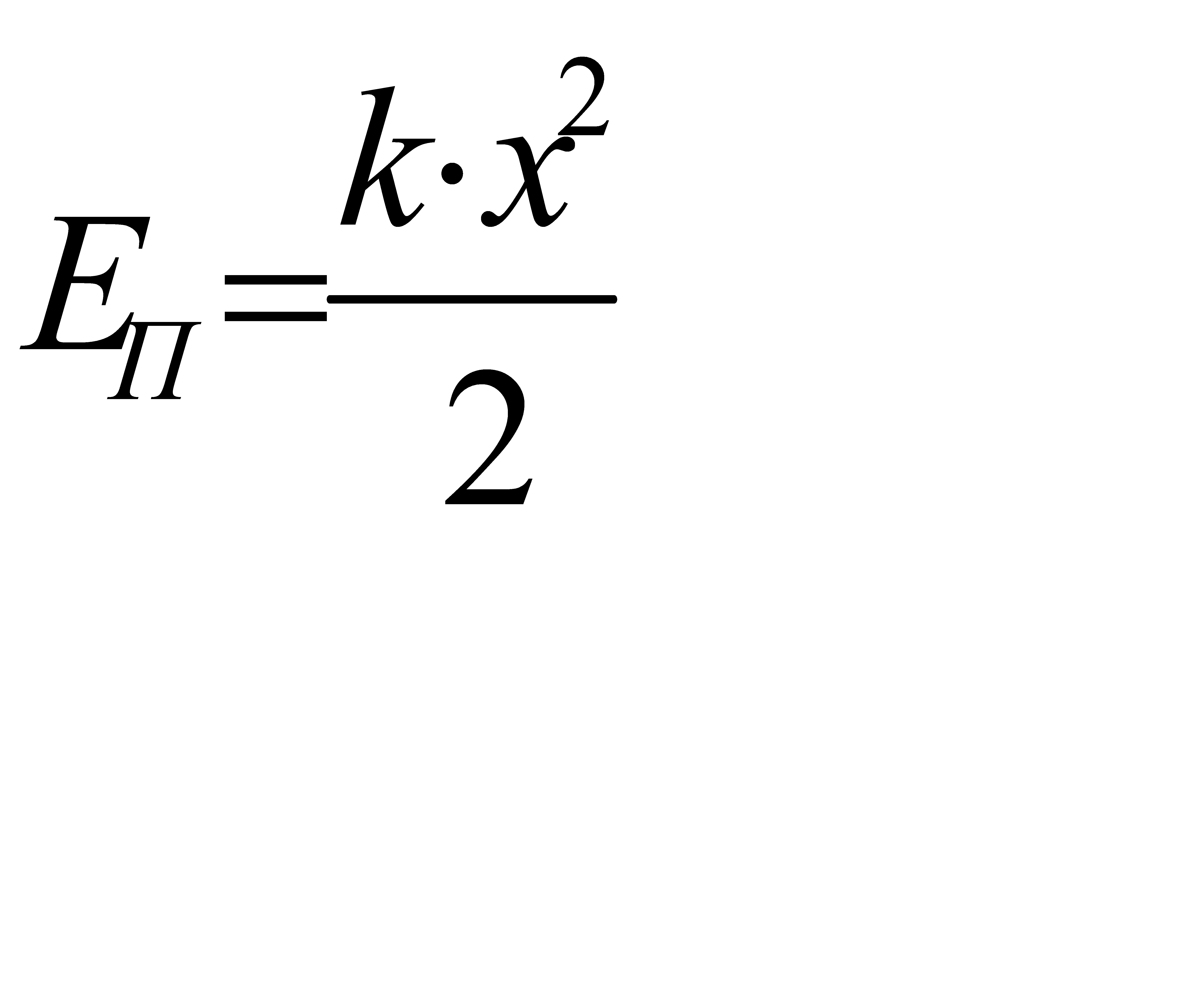 . Отложив на оси ординат полную механическую энергию Е, по графику определяют интервал координат (-А, +А), за пределы которого частица, обладающая такой энергией, выйти не может.
. Отложив на оси ординат полную механическую энергию Е, по графику определяют интервал координат (-А, +А), за пределы которого частица, обладающая такой энергией, выйти не может.
§6.2 Затухающие колебания
До сих пор мы рассматривали свободные колебания материальной точки без учёта сопротивления среды, в которой происходят эти колебания.
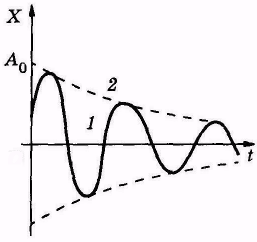
В реальных условиях на колеблющееся тело всегда действуют силы сопротивления (трения), в результате чего амплитуда с течением времени уменьшается и колебания становятся затухающими.
| Рис.5.8 |
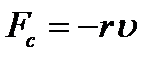 (5.13)
(5.13)
где r – коэффициент сопротивления среды, зависящий от плотности среды и геометрических размеров осциллятора; υ - относительная скорость движения осциллятора и среды.
Уравнение затухающих колебаний записывается в виде:
x = A0е-δt sin(ωt+φ0) (5.14)
Выражение А=±А0 е-δt , есть переменная во времени амплитуда колебания; А0— амплитуда в момент t = 0; ω -частота затухающих колебаний; φ0-начальная фаза колебаний.
| Рис. 6.9 |
Наглядной характеристикой затухания является отношение двух амплитуд, отличающихся по времени на период Т. Это соотношение называется декрементом затухания
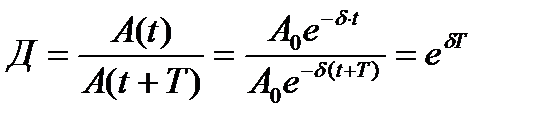 (5.15)
(5.15)
Прологарифмируем это выражение:
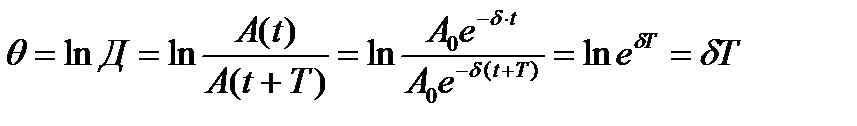 (5.16)
(5.16)
Значение θ=δТ называется логарифмическим декрементом затухания.
Время 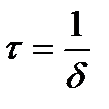 в течении которого амплитуда убывает в е раз, называется временем жизни колеблющейся точки. За время жизни τ система успевает совершить N колебаний.
в течении которого амплитуда убывает в е раз, называется временем жизни колеблющейся точки. За время жизни τ система успевает совершить N колебаний.
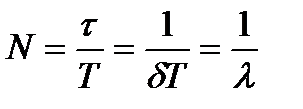 (5.17)
(5.17)
Следовательно, логарифмический декремент затухания есть величина, обратная числу колебаний осциллятора за время его жизни.
Период затухающих колебаний зависит от коэффициента сопротивления rи определяется формулой:
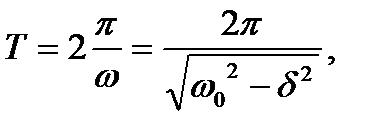 (5.18)
(5.18)
§6.3 Вынужденные колебания. Резонанс
Для того, чтобы колебания осциллятора были незатухающими, надо компенсировать потери энергии на преодоления сопротивления среды. Это можно сделать следующим способом. Пусть пружинный маятник с железным грузом находится в поле тяжести электромагнита, по обмотке которого проходит переменный ток:
I = I0 sin ωt (6.35)
Магнитная сила, действующая на маятник, меняется по тому же закону Fв=F0sinωt. Эта периодически изменяющаяся внешняя сила, действующая на осциллятор, называется вынуждающей силой.
Колебания, возникающие под действием внешней периодически изменяющейся силы, называют вынужденными колебаниями.
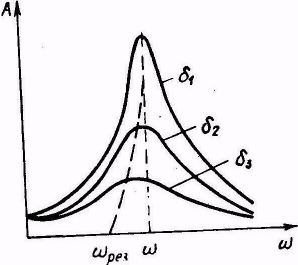
| Рис.6.11 |
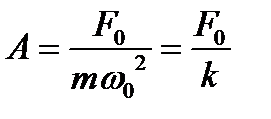 (6.42)
(6.42)
Когда частота вынуждающей силы приближается к частоте собственных колебаний осциллятора, амплитуда колебаний возрастает и при некоторой частоте достигает максимального значения. Это явление называется резонансом.
Существуют и такие колебательные системы, которые сами регулируют периодическое восполнение растраченной энергии и поэтому могут колебаться длительное время. Незатухающие колебания, существующие в какой-либо системе при отсутствии переменного внешнего воздействия, называются автоколебаниями, а сами системы — автоколебательными. Амплитуда и частота автоколебаний зависят от свойств самой автоколебательной системы, в отличие от вынужденных колебаний они не определяются внешними воздействиями.
Классическим примером механической автоколебательной системы являются часы, в которых маятник (или баланс) является колебательной системой, пружина (или поднятая гиря) — источником энергии, а анкер — регулятором поступления энергии от источника в колебательную систему. Некоторые биологические системы (сердце, легкие) являются автоколебательными.
Дата добавления: 2015-12-08; просмотров: 2894;
