Примеры решения задач. Пример 5.8.Запишите уравнение затухающих колебаний материальной точки, если смещение х0 точки при составляет 10см

Пример 5.8.Запишите уравнение затухающих колебаний материальной точки, если смещение х₀ точки при 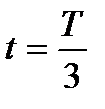составляет 10см, период затухающих колебаний Т=3с, логарифмический декремент затухания θ=0,03, начальная фаза колебаний равна нулю.

Дано: 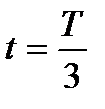; и х₀=10см=0,1м; Т= 3с; θ=0,03.

Найти: 1) х(t).

Решение. Уравнение затухающих колебаний, если начальная фаза равна нулю, имеет вид:

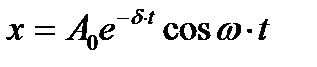, (1)

Где А₀ - амплитуда колебаний в момент времени t=0.

Циклическая частота

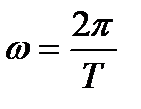(2)

Коэффициент затухания δ найдём из выражения для логарифмического декремента затухания: θ=δТ, откуда

.

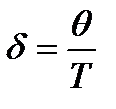Амплитуду А₀ найдём из начальных условий (х₀=10см при 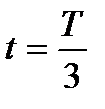=1с), согласно уравнению (1), где

,

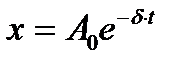откуда

.

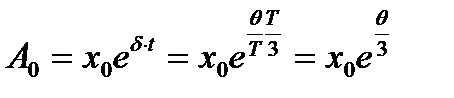Подставив в формулы (2), (3) и (4) заданные цифры найдём 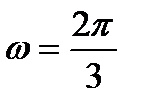с^-1; δ=0,01; А₀=10,1см. Тогда, подставив эти значения в уравнение (1), запишем искомое уравнение затухающих колебаний:

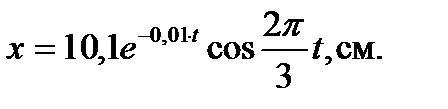
Ответ: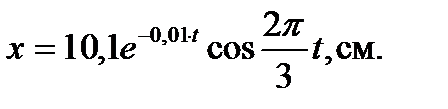

Пример 5.9.Маятник совершил 100 полных колебаний, при этом его амплитуда уменьшилась в 10 раз. Определить логарифмический декремент затухания маятника.

Дано: N=100; .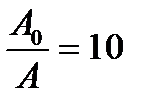

Найти: θ.

Решение. Логарифмический декремент затухания

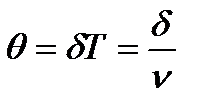, (1)

где 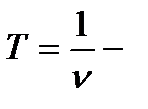условный период затухающих колебаний ( ν - частота колебаний); δ – коэффициент затухания.

Амплитуда затухающих колебаний в момент времени t=0.

Из формулы (1) найдём δ= ν θ, где частоту ν вычислим, зная число N полных колебаний за время t, за которое произошло указанное уменьшение амплитуды:

,

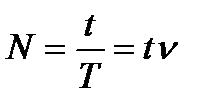откуда 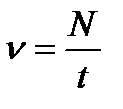и тогда

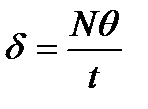. (3)

Подставив выражение (3) в формулу (2), получаем

,

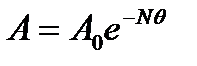Откуда искомый декремент затухания

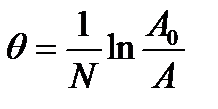
Ответ: θ=0,023

Пример 5.10.Логарифмический декремент θ затухания камертона, колеблющегося с частотой ν=100Гц, составляет 0,002. Определите промежуток времени, за который амплитуда возбужденного камертона уменьшится в 50 раз.

Дано: ν=100Гц; θ=0,002; .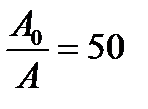

Найти: t.

Решение. Амплитуда затухающих колебаний изменяется со временем по закону

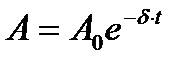, (1)

где А₀ – начальная амплитуда (в момент времени t=0); δ - коэффициент затухания.

Логарифмический декремент затухания θ =δТ, где 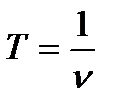- условный период затухающих колебаний. Тогда

δ=θ ν

и выражение (1) можно записать виде

,

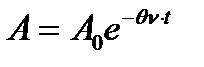откуда искомый промежуток времени

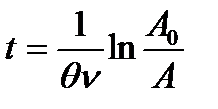
Ответ: t =19,6 с