ТЕМА 3. Многокритериальные задачи оптимизации
3.1 Корректная постановка многокритериальных задач
При необходимости одновременного учета нескольких критериев используются методы теории игр и исследования операций. Один из распространенных подходов, принадлежащий итальянскому экономисту Вильфредо Парето (1848-1923), состоит в отыскании нехудших решений.
Пусть необходимо найти решение, в котором желательно минимизировать несколько целевых функций:
min( f1(x),..., f p (x))
при условии x∈ X.
Допустимое решение ~x ∈ X называется эффективным по Парето или Парето-оптимальным, если не существует другого решения x∈ X такого, что fk (x) ≤ fk (~x ) для всех k = 1,…, p, и fi (x) < fi (~x ) хотя бы для одного i = 1,…, p.
Если x~ — эффективное решение, то ~y = f (~x ) называется недоминируемой точкой. Множество всех недоминируемых точек называется недоминируемым множеством и обозначается YN. Множество всех эффективных решений называется эффективным множеством и обозначается XE.
Понятие Парето-оптимального решения можно проиллюстрировать следующим примером. Пусть необходимо выбрать наиболее недорогой и экономичный автомобиль из вариантов, представленных в таблице.
| VW Golf | Opel Astra | Ford Focus | Toyota Corolla | |
| Цена | 16,2 | 14,9 | 14,0 | 15,2 |
| Расход топлива | 7,2 | 7,0 | 7,5 | 8,2 |
| Мощность |
Как видно из таблицы, критерии цены и экономичности взаимно противоречивы. Можно, однако, найти Парето-оптимальное решение.
На рисунке 3.1 данные из таблицы построены в осях «цена-расход топлива». Видно, что из всех вариантов Ford наиболее дешев, а Opel – наиболее экономичен. Варианты VW и Toyota не являются эффективными по Парето решениями (существуют варианты выбора, которые одновременно улучшают обе характеристики – цену и расход топлива).
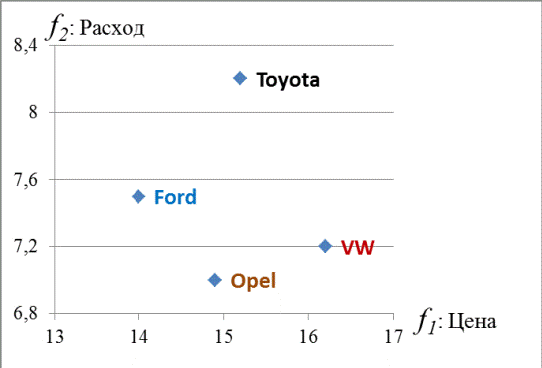
Рисунок 3.1 – К выбору эффективного по Парето решения
Если необходимо выбрать только один из двух полученных вариантов, векторный критерий должен быть свернут. Для этого следует проранжировать частные критерии по важности. Тогда вместо исходной многокритериальной задачи:
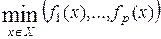
можно решать задачу с одним взвешенным критерием:
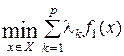
при разных значениях 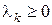 и
и 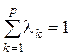 .
.
Другой подход к отысканию эффективного решения предоставляет метод уступок. Он основан на наложении ограничений на все целевые функции, кроме одной оставшейся.

Дата добавления: 2015-12-08; просмотров: 962;
