Оптимизация формы криволинейных стержней и балок

В качестве примера рассмотрим задачу определения оптимальной формы криволинейного стержня, нагруженного по всей длине горизонтально действующей погонной нагрузкой q, а на свободном конце – сосредоточенной вертикальной силой N (рисунок 5.1).

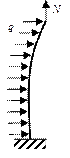
Рисунок 5.1 – Схема приложения сил к криволинейному стержню

Поставим задачу следующим образом: требуется определить такую форму оси стержня, при которой минимальна абсолютная величина изгибающего момента в наиболее нагруженном сечении.

Усилим критерий оптимизации, потребовав, чтобы в каждом сечении стержня изгибающий момент был равен нулю.

Выразим изгибающий момент в произвольном сечении, отстоящем от заделки по вертикали на расстояние y. Для этого примем неизвестное уравнение криволинейной оси стержня в виде: 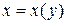, 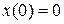. Момент в сечении складывается из момента вертикальной силы N и момента горизонтальной погонной нагрузки q:

.

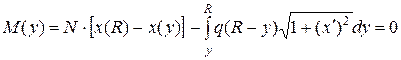Продифференцировав это равенство по координате y, получаем дифференциальное уравнение для определения формы оси стержня:

.

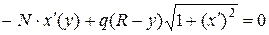Отсюда получаем:

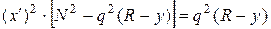
Окончательно, выразив из последнего уравнения производную x’ и проинтегрировав, получим:

.

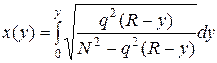Этот интеграл может быть вычислен приближенно.