Конечно-элементная модель статики, динамики и устойчивости конструкций

При оптимальном проектировании конструкций сложной геометрической формы, недостаточно точно описываемых традиционными расчетными схемами, естественно стремление использовать как можно более универсальную расчетную модель. В настоящее время наиболее разработанными и применимыми к наиболее широкому классу конструкций являются модели, основанные на конечно-элементном представлении.

Метод конечных элементов возник как обобщение классических методов строительной механики – метода сил и метода перемещений. Конструкция условно заменяется дискретной системой, состоящей из большого числа малых элементов простой формы – треугольников, прямоугольников, стержней, призм и т.п. Элементы взаимодействуют в узлах – точках, обычно находящихся в вершинах элементов, а в некоторых случаях и на их гранях.

Наиболее часто используется метод конечных элементов в форме метода перемещений. В нем основными переменными являются обобщенные перемещения узлов модели, а сопряженными переменными – обобщенные силы в узлах. Модель, в отличие от самой конструкции, имеет конечное число степеней свободы.

Статическое деформирование подчиняется вариационному принципу Лагранжа: из всех кинематически возможных полей перемещений, удовлетворяющих заданным условиям закрепления, то поле, которое доставляет минимум потенциальной энергии, обеспечивает также выполнение уравнений равновесия и граничных условий в усилиях (напряжениях).

Рассмотрим применение этого принципа к задаче теории упругости.

Построим кинематически возможные поля перемещений с помощью непрерывной интерполяции перемещений в каждом конечном элементе:

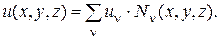(6.1)

Тогда деформации в элементе могут быть найдены путем дифференцирования перемещений по координатам:

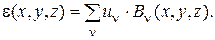(6.2)

Здесь B_n – блок матрицы деформаций B, содержащий производные базисных функций.

Напряжения в конечном элементе найдем, используя обобщенный закон Гука:

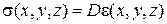. (6.3)

Энергия деформации одного элемента примет вид:

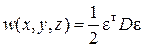, (6.4)

а потенциальная энергия всей дискретной модели

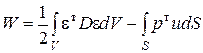. (6.5)

Подставляя в (6.5) равенства (6.2) и (6.3), получим:

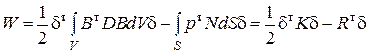. (6.6)

Здесь 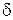- вектор перемещений всех узлов модели, K – матрица жесткости, R – вектор эквивалентных узловых сил.

Минимум квадратичной функции (6.6) найдем, приравнивая нулю все частные производные от потенциальной энергии по перемещениям узлов:

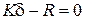. (6.7)

Матрица жесткости, входящая в левую часть (6.7), характеризует реакции упругой модели от единичных перемещений её узлов. Узловые перемещения 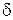можно найти, решив систему линейных уравнений (6.7). Порядок такой системы может быть высоким (десятки и сотни тысяч неизвестных), что требует использования компьютера и специализированного пакета программ.

В зависимости от формы и особенностей свойств моделируемой конструкции, выражения для матриц жесткости конкретизируются для различных типов конечных элементов. Приведем их для практически важного случая линейно-упругой криволинейно-ортотропной слоистой среды с переменными вдоль меридиана и по толщине свойствами.

Тело вращения относим к цилиндрической (глобальной) системе координат 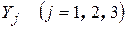и моделируем регулярной сеткой тороидальных изопараметрических конечных элементов второго порядка (рисунок 2.3).

Каждому КЭ ставим в соответствие локальную, масштабированную и естественную систему осей 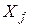так, чтобы при 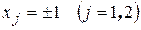координатные линии совпадали с границами элемента.

Зависимость между координатами точек КЭ в глобальном и локальном базисах записывается в виде [74, 131, 172]

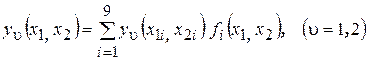, (2.74)

где 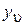− координаты узловых точек; 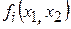− функция формы в локальной системе координат, определяемые выражениями

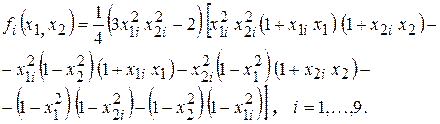(2.75)

Здесь 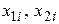— локальные координаты узловых точек КЭ, образующие матрицу

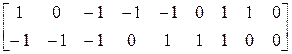. (2.76)

Рисунок 2.3 - Конечно-элементная аппроксимация тела вращения; квадратичный
изопараметрический конечный элемент второго порядка

Аналогично аппроксимируем перемещения КЭ, отнесенные к глобальному базису:

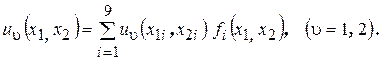, (2.77)

Деформированное состояние в произвольной точке КЭ описываем вектором

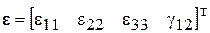, (2.78)

где индексы 1, 2, 3 — соответствуют направлениям осей .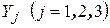

Соотношения между деформациями и перемещениями при осесимметричном нагружении имеют вид [99]:

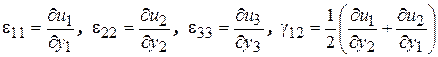. (2.79)

Введем вектор узловых перемещений КЭ

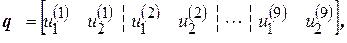(2.80)

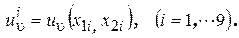(2.81)

В соответствии с формулами (2.74), (2.77) и (2.79) выводим:

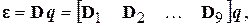(2.82)

где блочные матрицы

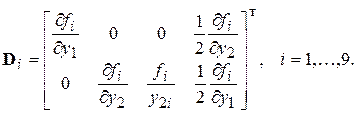(2.83)

Для вычисления частных производных 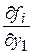и 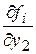воспользуемся зависимостями

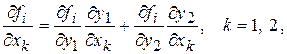(2.84)

которые представляем в матричной форме

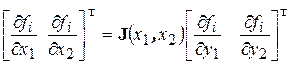. (2.85)

Здесь 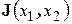− невырожденная ( 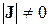) матрица Якоби:

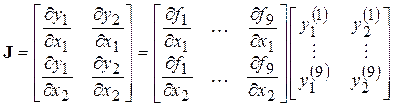, (2.86)

где обозначено

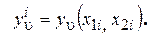(2.87)

Из выражения (2.85) найдем производные

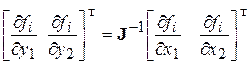. (2.88)

Подставляя зависимость (2.88) в формулу (2.82), имеем:

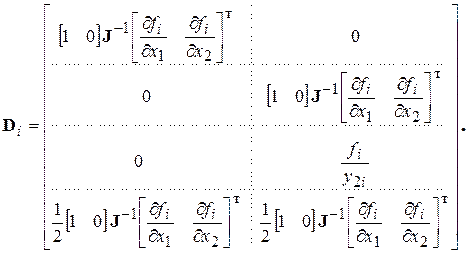(2.89)

Главные направления ортотропии материала КЭ совмещаем с местной ортогональной криволинейной системой осей 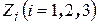, координатные линии и 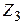которой совпадают соответственно с 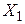и 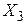, см. рис. 2.3. Направляющие косинусы осей 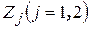по отношению к глобальной системе координат 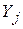определяются выражениями вида [5]

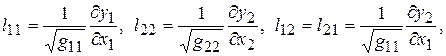(2.90)

где обозначено

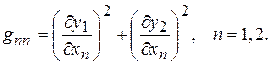(2.91)

Составляющие вектора деформации 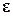образуют симметричный тензор второго ранга, компоненты которого при переходе к новой системе осей преобразуются по формуле

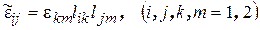. (2.92)

Используя выражения (2.82), (2.90) и (2.92), осуществим переход от компонент тензора деформаций, заданных в глобальной системе осей, к компонентам в осях 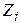. Результат представим в матричной форме (2.82):

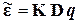, (2.93)

где 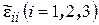− относительные удлинения отрезков, параллельных координатным осям ; 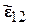− деформация сдвига, характеризующая изменение первоначально прямого угла между осям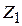и и ; матрица преобразования

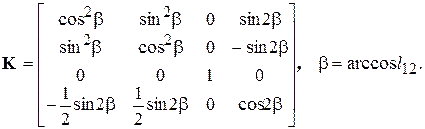(2.94)

В дальнейшей определяем деформации в осях . Поэтому ~ в обозначении 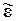опускаем.

Приращение вектора напряжений в материале при изменении расчётного состояния (изменение температуры или граничных условий, дополнительное нагружение) постулируем выражением

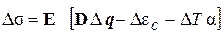. (2.95)

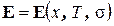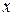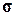Компоненты матрицы упругости считаем зависящими от координат , а также значений температуры и напряжений в элементе. Матрица 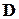преобразует вектор перемещений 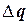узлов КЭ в вектор упругих деформаций, отнесенных к местным осям, см. формулу (2.82).

Для ортотропного материала, исключая из рассмотрения две деформации сдвига, нарушающие осевую симметрию, имеем:

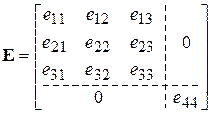. (2.96)

Зависимости компонентов 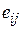от модулей упругости и коэффициентов Пуассона имеют вид [99]:

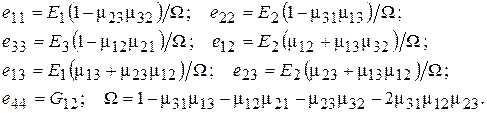(2.97)

Для составления матрицы жёсткости КЭ запишем вариационное уравнение равновесия, соответствующее некоторому расчётному состоянию изделия:

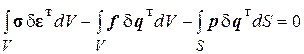, (2.98)

где 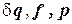− векторы возможных перемещений, объёмных и поверхностных усилий в узлах КЭ в глобальном базисе; 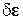, 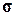− векторы деформаций и напряжений в осях 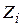; 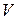− объём, занимаемый КЭ; 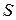− площадь поверхности элемента, к которой приложена поверхностная нагрузка.

Учитывая выражения (2.82) и (2.93), запишем:

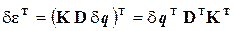, (2.99)

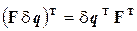. (2.100)

Здесь 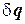− возможные перемещения узловых точек КЭ. Матрица

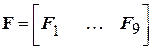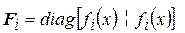, . (2.101)

Подставляя в условие (2.98) зависимость (2.95), получим уравнение

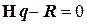, (2.102)

где матрица жёсткости элемента в глобальной системе координат

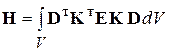, (2.103)

соответствующий вектор обобщённых воздействий, приведённых к узлам элемента

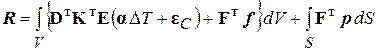. (2.104)

Физико-механические характеристики материала, температуру и нагрузки, изменяющиеся в пределах КЭ, задаём в узловых точках с последующей интерполяцией по формулам типа

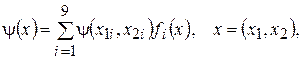
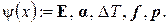(2.105)

Для вычисления интегралов в выражениях (2.103) и (2.104) используем квадратурные формулы Гаусса [131]. Тогда выражения (2.103) и (2.104) преобразуются к виду:

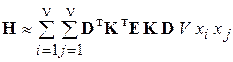; (2.115)

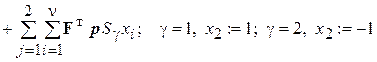. (2.116)

Таким образом, разрешающие уравнения задачи статического деформирования имеют вид системы линейных или нелинейных уравнений относительно обобщенных перемещений узлов конструкции, в которой коэффициенты системы образуют матрицу жесткости и получаются по формулам (2.116), а правые части определяются силовыми и температурными воздействиями

Методы, основанные на конечно-элементных представлениях, являются математически обоснованными приближенными методами решения задач теории упругости, теории пластин, теории оболочек. Вопросы обоснования и оценки точности подробно описаны в специальной литературе. Целесообразно привести здесь следующие основные факты.

1. При отсутствии в точном решении задачи теории упругости особых точек, в которых напряжения бесконечны, правильно построенные уравнения метода конечных элементов дают решение, сходящееся к точному при неограниченном сгущении сетки конечных элементов.

2. Скорость сходимости определяется уменьшением погрешности при удвоении сетки конечных элементов и характеризуется порядком сходимости – показателем степени p в соотношении:

,

где - погрешность приближенного решения,

h – максимальный размер конечного элемента (параметр сетки).

3. Порядок сходимости находится теоретически в виде асимптотической оценки, в пределе сгущения сетки. Асимптотический порядок сходимости зависит от типа используемых конечных элементов. Обычно элементы, имеющие меньшее число узлов, дают и меньший порядок сходимости.

4. Фактическая точность численного решения зависит от размеров элементов, соотношений углов конечных элементов, вида элементов и вида рассчитываемой конструкции, нагрузок и условий закрепления. Приближенная оценка точности полученного решения в практически важных случаях может быть получена по правилу Рунге:

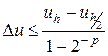, (6.10)

где 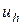- приближенное решение на сетке с размерами элементов h,

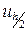- приближенное решение на «удвоенной» сетке с размерами элементов h/2,

p – эффективный порядок сходимости.

Эффективный порядок, в отличие от асимптотического, оценивается проведением серии расчетов с последовательным удвоением сетки.

Следует с осторожностью относиться к выбору конечно-элементной модели конструкции. Несмотря на теоретическую общность представленного математического аппарата, матрицы жесткости разных элементов конструкций имеют различные представления.

Рассмотрим, далее, модель динамического деформирования конструкции. Любые нестационарные движения – колебания, волновые процессы, удар – требуют учета при анализе как упругих свойств конструкции, так и её инерции. Теоретическую основу решения можно получить, используя вариационные принципы классической механики. Удобно получить уравнение движения конечно-элементной модели из уравнения Лагранжа 2-го рода.

При малых амплитудах колебаний в результате получается следующее дифференциальное уравнение:

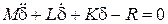. (6.11)

Здесь M – матрица масс, а L – матрица демпфирования.

В отличие от уравнения (6.10), внешние узловые силы R могут зависеть от времени.

Решение системы уравнений (6.11) может быть найдено численно. Однако больший интерес во многих случаях представляет не решение, а исследование этой системы. Так, практически важно при проектировании конструкции оценить её резонансные частоты. Для этого достаточно найти решения однородной системы, при R=0, или решить характеристическое уравнение:

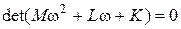. (6.12)

Методы решения таких уравнений описаны в литературе по методу конечных элементов.

Наконец, рассмотрим нелинейное поведение и потерю устойчивости конечно-элементной модели конструкции. Условие бифуркации решения (эйлеровой потери устойчивости) имеет вид:

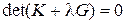. (6.13)

Здесь G – матрица геометрической жесткости модели, которая характеризует нелинейное изменение реакций при малых вариациях перемещений из достигнутого докритического равновесного состояния. Корень характеристического уравнения (6.13) равен отношению критической нагрузки потери устойчивости к расчетной нагрузке, при которой получена матрица геометрической жесткости.

Итак, конечно-элементные модели статики, динамики и устойчивости конструкций приводят к необходимости численного компьютерного решения уравнений высокого порядка. Это затрудняет их непосредственное использование в оптимальном проектировании.