Задача максимизации прочности при заданной массе

Рассмотрим эту же конструкцию с других позиций. Пусть масса трехстержневой фермы M задана, а требуется распределить материал так, чтобы при заданном виде нагрузки несущая способность была максимальной.

Целевую функцию построим следующим образом. При пробной (единичной) нагрузке, приложенной к нижнему узлу фермы по горизонтали, в стержнях возникают напряжения. Увеличение нагрузки в некоторое число раз Q приведет к пропорциональному росту напряжений. Разрушение произойдет, когда хотя бы в одном стержне напряжения достигнут предела прочности. Таким образом, несущая способность фермы будет равна

. (2.6)

Требуется найти площади сечений, доставляющие максимум функции Q при ограничениях:

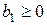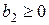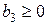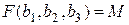, , , . (2.7)

Эту задачу для численного решения удобнее переформулировать. Используя ограничение-равенство, выразим из него одну из искомых площадей, например, площадь сечения третьего стержня:

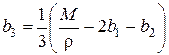. (2.8)

Теперь у нас осталось две независимые переменные. Положим целевую функцию равной нулю, если хотя бы одна из площадей сечений отрицательна, и исследуем изменение несущей способности при варьировании двух независимых переменных – b₁ и b₂. График полученной функции для массы, равной 0,5 кг, приведен на рисунке 2.3. Из графика видно, что максимум несущей способности получается при выборе b₂=0, что согласуется с решением предыдущего примера.

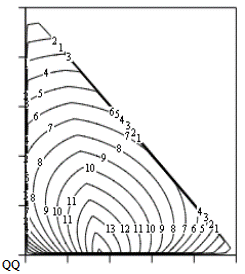
Рисунок 2.3 – Изолинии несущей способности при варьировании площадей сечений двух первых стержней