Задача проектирования равнопрочной конструкции

Предыдущие примеры показывают, что оптимальной оказывается та конструкция, в которой весь материал нагружен предельно допустимыми напряжениями. Таким образом, можно предложить ещё один частный критерий оптимальности, состоящий в минимуме отклонения действующих напряжений от предельно допустимых. Вопрос о выборе допустимых напряжений сводится к назначению коэффициента запаса по напряжениям и коэффициента безопасности по расчетным нагрузкам, а в случае сложного напряженного состояния дополнительно должен быть задан критерий прочности.

Таким образом, получаем следующую постановку задачи оптимизации: найти такое сочетание варьируемых конструктивных параметров, при котором отношение действующих напряжений к предельным одинаково во всех точках конструкции.

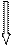
а б в

Рисунок 2.4 – Равнопрочная консольная балка: а – схема нагружения, б – размеры сечения, в – закон изменения ширины сечения.

Дана конструктивно-силовая схема (рисунок 2.4), длина балки и строительная высота сечения h. Требуется по критерию равнопрочности найти закон изменения ширины прямоугольного сечения.

Для решения этой задачи найдем вначале распределение изгибающего момента:

. (2.9)

Отсюда максимальные напряжения в сечении, отстоящем на расстояние x от заделки, равны

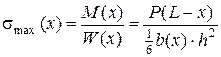. (2.10)

Приравнивая полученные напряжения к пределу прочности на растяжение, получим:

. (2.11)

Таким образом, равнопрочная по нормальным напряжениям балка должна иметь треугольную форму в плане. Однако при поперечном изгибе в балке действуют не только нормальные, но и касательные напряжения, определяемые по формуле Журавского:

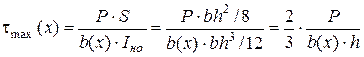. (2.12)

Приняв критерий прочности по максимальным напряжениям (т.е. считая разрушение от растяжения и сдвига происходящими независимо), получим, что по условию прочности на сдвиг ширина сечения должна быть постоянной и равной следующей величине:

. (2.13)

Так как балка не должна разрушаться ни от нормальных, ни от касательных напряжений, окончательно получаем следующий закон изменения ширины сечений (рисунок 2.4, в):

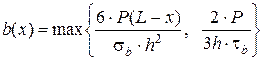. (2.14)

Критерий равнопрочности, вообще говоря, отличается от критериев минимума массы и максимума несущей способности. Однако для ряда практически важных случаев доказана их равносильность.