Задачи параметрической оптимизации

Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ* , который доставляет минимальное значение f(χ*) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации необходимо задать:

Допустимое множество — множество ;

Целевую функцию — отображение ;

Критерий поиска (max или min).

Тогда решить задачу 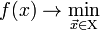означает одно из:

1. Показать, что .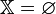

2. Показать, что целевая функция 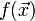не ограничена снизу.

3. Найти .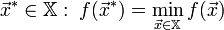

4. Если , то найти .

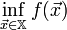Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек x₀ таких, что всюду в некоторой их окрестности 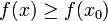для минимума и для максимума.

Если допустимое множество , то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.

Ограничения могут быть сформулированы в виде неравенств (когда параметры конструкции не могут превышать некоторых пределов или быть меньше некоторых минимально допустимых величин) и в виде равенств (когда некоторые величины, характеризующие конструкцию, заранее заданы).