Классификация методов оптимизации
Общая запись задач оптимизации задаёт большое разнообразие их классов. От класса задачи зависит подбор метода (эффективность её решения). Классификацию задач определяют: целевая функция и допустимая область (задаётся системой неравенств и равенств или более сложным алгоритмом).
Методы оптимизации классифицируют в соответствии с задачами оптимизации:
Локальные методы: сходятся к какому-нибудь локальному экстремуму целевой функции. В случае унимодальной целевой функции, этот экстремум единственен, и будет глобальным максимумом/минимумом.
Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.
Существующие в настоящее время методы поиска можно разбить на три большие группы:
· детерминированные;
· случайные (стохастические);
· комбинированные.
По критерию размерности допустимого множества, методы оптимизации делят на методы одномерной оптимизации и методы многомерной оптимизации.
По виду целевой функции и допустимого множества, задачи оптимизации и методы их решения можно разделить на следующие классы:
· Задачи оптимизации, в которых целевая функция 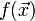 и ограничения
и ограничения 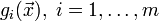 являются линейными функциями, разрешаются так называемыми методами линейного программирования.
являются линейными функциями, разрешаются так называемыми методами линейного программирования.
· В противном случае имеют дело с задачей нелинейного программирования и применяют соответствующие методы. В свою очередь из них выделяют две частные задачи:
· если 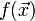 и
и 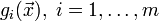 — выпуклые функции, то такую задачу называют задачей выпуклого программирования;
— выпуклые функции, то такую задачу называют задачей выпуклого программирования;
· если 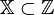 , то имеют дело с задачей целочисленного (дискретного) программирования.
, то имеют дело с задачей целочисленного (дискретного) программирования.
По требованиям к гладкости и наличию у целевой функции частных производных, их также можно разделить на:
· прямые методы, требующие только вычислений целевой функции в точках приближений;
· методы первого порядка: требуют вычисления первых частных производных функции;
· методы второго порядка: требуют вычисления вторых частных производных, то есть гессиана целевой функции.
Помимо того, оптимизационные методы делятся на следующие группы:
· аналитические методы (например, метод множителей Лагранжа и условия Каруша-Куна-Таккера);
· численные методы;
· графические методы.
В зависимости от природы множества X задачи математического программирования классифицируются как:
· задачи дискретного программирования (или комбинаторной оптимизации) — если X конечно или счётно;
· задачи целочисленного программирования — если X является подмножеством множества целых чисел;
· задачей нелинейного программирования, если ограничения или целевая функция содержат нелинейные функции и X является подмножеством конечномерного векторного пространства.
· Если же все ограничения и целевая функция содержат лишь линейные функции, то это — задача линейного программирования.
Кроме того, разделами математического программирования являются параметрическое программирование, динамическое программирование и стохастическое программирование. Математическое программирование используется при решении оптимизационных задач исследования операций.
Способ нахождения экстремума полностью определяется классом задачи. Но перед тем, как получить математическую модель, нужно выполнить 4 этапа моделирования:
1. Определение границ системы оптимизации: отбрасываем те связи объекта оптимизации с внешним миром, которые не могут сильно повлиять на результат оптимизации, а, точнее, те, без которых решение упрощается
2. Выбор управляемых переменных: «замораживаем» значения некоторых переменных (неуправляемые переменные). Другие оставляем принимать любые значения из области допустимых решений (управляемые переменные)
3. Определение ограничений на управляемые переменные (равенства и/или неравенства)
4. Выбор числового критерия оптимизации (создаём целевую функцию).
Дата добавления: 2015-12-08; просмотров: 2792;
