Оптимизация потока с критическими работами, выявленными с учетом ресурсных и фронтальных связей
Алгоритм оптимизации потока с критическими работами, выявленный с учета ресурсных и фронтальных связей по критерию достижения минимальной продолжительности всего комплекса работ, является общим (универсальным), то есть соответствует не только данной разновидности потоков, но и потоку с критическими работами, выявленными с учетом ресурсных, фронтальных и прямых ранговых связей, а также с ресурсными, фронтальными и обратными ранговыми связями.
В последних двух случаях специфика учитывается только в заключительной части расчета при определении реальной продолжительности потоков с учетом соответствующих видов связей.
Алгоритм предполагает определение ПВМП у каждой промежуточной матрицы путем принудительного направления критического пути поочередно по каждой незафиксированной строке и каждому столбцу с определенным учетом зафиксированных работ и минимально возможных предшествующих и последующих незафиксированных работ. При этом число ПВМП у каждой матрицы равно сумме числа незафиксированных строк и всех столбцов, а в расчет принимается максимальная величина ПВМП, как наиболее близкая к реальной продолжительности.
Алгоритм заключается в следующем:
1. Представляются исходные данные на матрице в системе ОФР.
2. Формируется порфириан и определяется ПВМП в результате формирования и расчета промежуточных матриц при прогоне критического пути по фронтальным комплексам (строкам) и видам работ (столбцам).
3. Определяется расчетное значение ПВМП у каждой промежуточной (условной) матрицы.
4. Формируются конечные (реальные) матрицы.
5. Определяется Т.
Проиллюстрируем методику оптимизации потока с критическими работами при тех же исходных данных (использованных в рассмотренных выше примерах).
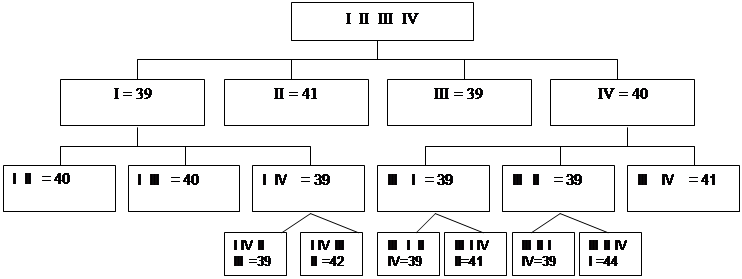
 |
Рис. 28. Порфириан оптимизации потока с КР.
Таким образом, в данном случае выявлены в качестве оптимальных очередностей освоения фронтов I, IV, II, III; III, I, II, IV и III, II, I, IV, обеспечивающие минимальную продолжительность потока равную 39 ед. времени. Для этого потребовалось сформировать и рассчитать 10 промежуточных матриц и 6 конечных (вместо 24, соответствующих полному перебору).
Рассмотрим приведенные ниже промежуточные и конечные матрицы с результатами их расчета, обратив внимание на то, что промежуточные матрицы представлены в системе ОФР и дополнены столбцами и строками, в которых указываются продолжительности незафиксированных строк и незафиксированных работ в столбцах (Σ), продолжительность (минимально возможная) предшествующих и последующих критическим строкам и столбцам работ и их суммарная величина, то есть ПВМП.
Определение Σ комментариев не требует. Δ при прохождении критического пути по незафиксированной строке включает в себя продолжительность зафиксированных работ первого вида и, возможно, незафиксированных работ первого вида в других строках, если они меньше продолжительности работ последнего вида в тех же строках, а также продолжительность незафиксированных работ последнего вида, если они меньше продолжительности работ первого вида в первых строках.
Δ при прохождении критического пути по столбцу включает в себя срок окончания последней по очереди зафиксированной работы, а также возможную минимальную продолжительность завершающих работ в предположении, что каждая незафиксированная строка может быть помещена на последнее место.
| А | Б | В | Г | ||||
| 0 4 | 4 6 | 6 13 | 13 18 | ||||
| I | Σ | Δ | ПВМП | ||||
| Σ | |||||||
| Δ | max ПВМП = 39 | ||||||
| ПВМП |
| А | Б | В | Г | ||||
| 0 5 | 5 8 | 8 17 | 17 23 | ||||
| II | Σ | Δ | ПВМП | ||||
| Σ | |||||||
| Δ | max ПВМП = 41 | ||||||
| ПВМП |
| А | Б | В | Г | ||||
| 0 5 | 3 5 | 5 13 | 13 16 | ||||
| III | Σ | Δ | ПВМП | ||||
| Σ | |||||||
| Δ | max ПВМП = 39 | ||||||
| ПВМП |
| А | Б | В | Г | ||||
| IV | 0 4 | 4 7 | 7 13 | 13 17 | |||
| Σ | Δ | ПВМП | |||||
| Σ | |||||||
| Δ | max ПВМП = 40 | ||||||
| ПВМП |
| А | Б | В | Г | ||||
| I | 0 4 | 4 6 | 6 13 | 13 18 | |||
| II | 5 10 | 10 13 | 13 22 | 22 28 | |||
| Σ | Δ | ПВМП | |||||
| Σ | |||||||
| Δ | max ПВМП = 40 | ||||||
| ПВМП |
| А | Б | В | Г | ||||
| I | 0 4 | 4 6 | 6 13 | 13 18 | |||
| III | 8 11 | 11 13 | 13 21 | 21 29 | |||
| Σ | Δ | ПВМП | |||||
| Σ | |||||||
| Δ | max ПВМП = 40 | ||||||
| ПВМП |
| А | Б | В | Г | ||||
| I | 0 4 | 4 6 | 6 13 | 13 18 | |||
| IV | 6 10 | 10 13 | 13 19 | 19 23 | |||
| Σ | Δ | ПВМП | |||||
| Σ | |||||||
| Δ | max ПВМП = 39 | ||||||
| ПВМП |
| А | Б | В | Г | ||||
| III | 0 5 | 3 5 | 5 13 | 13 16 | |||
| I | 7 11 | 11 13 | 13 20 | 20 25 | |||
| Σ | Δ | ПВМП | |||||
| Σ | |||||||
| Δ | max ПВМП = 39 | ||||||
| ПВМП |
| А | Б | В | Г | ||||
| III | 0 3 | 3 5 | 5 13 | 13 16 | |||
| II | 5 10 | 10 13 | 13 22 | 22 28 | |||
| Σ | Δ | ПВМП | |||||
| Σ | |||||||
| Δ | max ПВМП = 39 | ||||||
| ПВМП |
| А | Б | В | Г | ||||
| III | 0 3 | 3 5 | 5 13 | 13 16 | |||
| IV | 6 10 | 10 13 | 13 19 | 19 23 | |||
| Σ | Δ | ПВМП | |||||
| Σ | |||||||
| Δ | max ПВМП = 41 | ||||||
| ПВМП |
Рис. 29. Промежуточные (условные) матрицы.
| ОФР | А | Б | В | Г | ОФР | А | Б | В | Г | ОФР | А | Б | В | Г | ||
| I | 0 4 | 4 6 | 6 13 | 13 18 | I | 0 4 | 4 6 | 6 13 | 13 18 | III | 0 3 | 3 5 | 5 13 | 13 16 | ||
| IV | 4 8 | 8 11 | 13 19 | 19 23 | IV | 4 8 | 8 11 | 13 19 | 19 23 | I | 3 7 | 7 9 | 13 20 | 20 25 | ||
| III | 8 11 | 11 13 | 19 27 | 27 30 | II | 8 13 | 13 16 | 19 28 | 28 34 | II | 7 12 | 12 15 | 20 29 | 29 35 | ||
| II | 11 16 | 16 19 | 27 36 | 36 42 | III | 13 16 | 16 18 | 28 36 | 36 39 | IV | 12 16 | 16 18 | 28 36 | 36 39 | ||
| ОФР | А | Б | В | Г | ОФР | А | Б | В | Г | ОФР | А | Б | В | Г | ||
| III | 0 3 | 3 5 | 5 13 | 13 22 | III | 0 3 | 3 5 | 5 13 | 13 16 | III | 0 3 | 3 5 | 5 13 | 13 16 | ||
| I | 3 7 | 7 9 | 13 20 | 22 27 | II | 5 10 | 10 13 | 13 22 | 22 28 | II | 5 10 | 10 13 | 13 22 | 22 28 | ||
| IV | 7 11 | 11 14 | 20 26 | 27 31 | I | 16 20 | 20 22 | 22 29 | 29 34 | IV | 15 19 | 19 22 | 22 28 | 28 32 | ||
| II | 11 16 | 16 19 | 26 35 | 35 41 | IV | 22 26 | 26 29 | 29 35 | 35 39 | I | 22 26 | 26 28 | 28 35 | 35 40 | ||
Рис. 30. Конечные (реальные) матрицы.
Дата добавления: 2015-12-08; просмотров: 1022;
