Порфириан оптимизации потока с НОФ
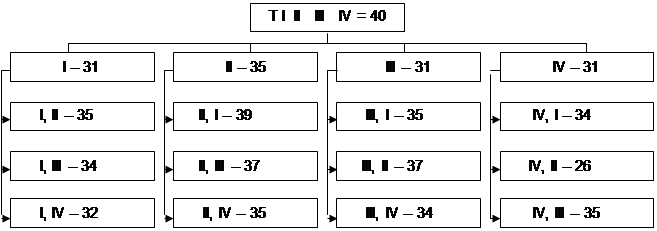
Ниже дальнейшее развитие порфириана.
| I, IV, II, III – 39 | I, IV, III, II – 40 | ||
| I, III, II, IV – 40 | I, III, IV, II – 40 | ||
| III, IV, I, II – 41 | III, IV, II, I – 40 | ||
| IV, I, II, III – 40 | IV, I, III, II – 43 | ||
| I, II, III, IV – 40 | I, II, IV, III – 39 | ||
| III, I, II, IV – 39 | III, I, IV, II – 41 | ||
| IV, III, I, II – 43 | IV, III, II, I – 42 | ||
| II, IV, I, III – 41 | II, IV, III, I – 43 | ||
| IV, II, I, III – 40 | IV, II, III, I – 42 | ||
| II, III, I, IV – 42 | II, III, IV, I – 43 | ||
| III, II, I, IV – 39 | III, II, IV, I – 40 | ||
| II, I, III, IV – 42 | II, I, IV, III – 41 |
Рис. 20. Порфириан оптимизации потока с НОФ.
Рассмотрим приведенные ниже промежуточные и конечные матрицы, соответствующие данному порфириану, с результатами их расчета.
| А | Б | В | Г | А | Б | В | Г | |||||||
| 0 4 | 4 6 | 6 13 | 13 18 | 0 5 | 5 8 | 8 17 | 17 23 | |||||||
| I | II | |||||||||||||
| 18 + 6 + 3 + 4 = 31 | 23 + 5 + 3 + 4 = 35 | |||||||||||||
| ПВМП = 31 | ПВМП = 35 | |||||||||||||
| А | Б | В | Г | А | Б | В | Г | |||||||
| 0 3 | 3 5 | 5 13 | 13 16 | 0 4 | 4 7 | 7 13 | 13 17 | |||||||
| III | IV | |||||||||||||
| 16 + 5 + 6 + 4 = 31 | 17 + 5 + 6 + 3 = 31 | |||||||||||||
| ПВМП = 31 | ПВМП = 31 | |||||||||||||
| А | Б | В | Г | А | Б | В | Г | |||||||
| 0 4 | 4 6 | 6 13 | 13 18 | 0 4 | 4 6 | 6 13 | 13 18 | |||||||
| I | I | |||||||||||||
| 5 10 | 10 13 | 13 22 | 22 28 | 8 11 | 11 13 | 13 21 | 21 24 | |||||||
| II | III | |||||||||||||
| 28 + 3 + 4 = 35 | 24 + 6 + 4 = 34 | |||||||||||||
| ПВМП = 35 | ПВМП = 34 | |||||||||||||
| А | Б | В | Г | А | Б | В | Г | |||||||
| 0 3 | 3 5 | 5 13 | 13 16 | 0 3 | 3 5 | 5 13 | 13 16 | |||||||
| III | III | |||||||||||||
| 5 10 | 10 13 | 13 22 | 22 28 | 6 10 | 10 13 | 13 19 | 19 23 | |||||||
| II | IV | |||||||||||||
| 28 + 5 + 4 = 37 | 23 + 5 + 6 = 34 | |||||||||||||
| ПВМП = 37 | ПВМП = 34 | |||||||||||||
| А | Б | В | Г | А | Б | В | Г | |||||||
| 0 4 | 4 7 | 7 13 | 13 17 | 0 4 | 4 7 | 7 13 | 13 17 | |||||||
| IV | IV | |||||||||||||
| 7 9 | 9 13 | 13 20 | 20 25 | 5 10 | 10 13 | 13 22 | 22 28 | |||||||
| I | II | |||||||||||||
| 25 + 6 + 3 = 34 | 28 + 5 + 3 = 36 | |||||||||||||
| ПВМП = 34 | ПВМП = 36 | |||||||||||||
| А | Б | В | Г | |||
| 0 4 | 4 7 | 7 13 | 13 17 | |||
| IV | ||||||
| 8 11 | 11 13 | 13 21 | 21 24 | |||
| III | ||||||
| 24 + 5 + 6 = 35 | ||||||
| ПВМП = 35 | ||||||
Рис. 21. Промежуточные (условные) матрицы.
Конечные (реальные) матрицы
| ОФР | А | Б | В | Г | ОФР | А | Б | В | Г | |
| I | 0 4 | 4 6 | 6 13 | 13 18 | I | 0 4 | 4 6 | 6 13 | 13 18 | |
| IV | 6 10 | 10 13 | 13 19 | 19 23 | IV | 6 10 | 10 13 | 13 19 | 19 23 | |
| II | 11 16 | 16 19 | 19 28 | 28 34 | III | 14 17 | 17 19 | 19 27 | 27 30 | |
| III | 23 26 | 26 28 | 28 36 | 36 39 | II | 19 24 | 24 27 | 27 36 | 36 40 | |
| ОФР | А | Б | В | Г | ОФР | А | Б | В | Г | |
| I | 0 4 | 4 6 | 6 13 | 13 18 | I | 0 4 | 4 6 | 6 13 | 13 18 | |
| III | 8 11 | 11 13 | 13 21 | 21 24 | III | 8 11 | 11 13 | 13 19 | 19 22 | |
| II | 13 18 | 18 21 | 21 30 | 30 36 | IV | 12 16 | 16 19 | 19 25 | 25 29 | |
| IV | 23 27 | 27 30 | 30 36 | 36 40 | II | 17 22 | 22 25 | 25 34 | 34 40 | |
| ОФР | А | Б | В | Г | ОФР | А | Б | В | Г | |
| III | 0 3 | 3 5 | 5 13 | 18 16 | III | 0 3 | 3 5 | 5 13 | 13 16 | |
| IV | 6 10 | 10 13 | 13 19 | 19 23 | IV | 6 10 | 10 13 | 13 19 | 19 22 | |
| I | 13 17 | 17 19 | 19 26 | 26 31 | II | 11 16 | 16 19 | 19 28 | 28 34 | |
| 18 23 | 23 26 | 26 35 | 35 41 | 23 26 | 26 28 | 28 35 | 35 40 | |||
| II | I |
| ОФР | А | Б | В | Г | ОФР | А | Б | В | Г | |
| IV | 0 4 | 4 7 | 7 13 | 13 17 | IV | 0 4 | 4 7 | 7 13 | 13 17 | |
| I | 7 11 | 11 13 | 13 20 | 20 25 | I | 7 11 | 11 13 | 13 20 | 20 25 | |
| II | 12 17 | 17 20 | 20 29 | 29 35 | III | 15 18 | 18 20 | 20 28 | 28 31 | |
| III | 24 27 | 27 29 | 29 37 | 37 40 | II | 20 25 | 25 28 | 28 37 | 37 43 | |
| ОФР | А | Б | В | Г | ОФР | А | Б | В | Г | |
| I | 0 4 | 4 6 | 6 13 | 13 18 | I | 0 4 | 4 6 | 6 13 | 13 18 | |
| II | 5 10 | 10 13 | 13 22 | 22 28 | II | 5 10 | 10 13 | 13 22 | 22 28 | |
| III | 17 20 | 20 22 | 22 30 | 30 33 | IV | 15 19 | 19 22 | 22 28 | 28 32 | |
| IV | 23 27 | 27 30 | 30 36 | 36 40 | III | 23 26 | 26 28 | 28 36 | 36 39 | |
| ОФР | А | Б | В | Г | ОФР | А | Б | В | Г | |
| III | 0 3 | 3 5 | 5 13 | 18 16 | III | 0 3 | 3 5 | 5 13 | 13 16 | |
| I | 7 11 | 11 13 | 13 20 | 20 25 | I | 7 11 | 11 13 | 13 20 | 20 25 | |
| II | 12 17 | 17 20 | 20 29 | 29 35 | IV | 13 17 | 17 20 | 20 26 | 26 30 | |
| 22 26 | 26 29 | 29 35 | 35 39 | 18 23 | 23 26 | 26 35 | 35 41 | |||
| IV | II |
| ОФР | А | Б | В | Г | ОФР | А | Б | В | Г | |
| IV | 0 4 | 4 7 | 7 13 | 13 17 | IV | 0 4 | 4 7 | 7 13 | 13 17 | |
| III | 8 11 | 11 13 | 13 21 | 21 24 | III | 8 11 | 11 13 | 13 21 | 21 24 | |
| I | 15 19 | 19 21 | 21 28 | 28 33 | II | 13 18 | 18 21 | 21 30 | 30 36 | |
| 20 25 | 25 28 | 28 37 | 37 43 | 24 28 | 28 30 | 30 37 | 37 42 | |||
| II | I |
Рис. 22. Конечные (реальные) матрицы.
В связи с тем, что брошенная развитием матрица первого уровня (с закрепленной на первом месте второй строки), имеет ПВМВ равный 35, а наименьшая реальная продолжительность потока равна 39 ед. времени, необходимо продолжить ее развитие.
Промежуточные (условные) матрицы
| А | Б | В | Г | А | Б | В | Г | |||||||
| 0 5 | 5 8 | 8 17 | 17 23 | 0 5 | 5 8 | 8 17 | 17 23 | |||||||
| II | II | |||||||||||||
| 11 15 | 15 17 | 17 24 | 24 29 | 12 15 | 15 17 | 17 25 | 25 2 8 | |||||||
| I | III | |||||||||||||
| 29 + 3 + 4 = 36 | 28 + 5 + 4 = 37 | |||||||||||||
| ПВМП = 39 | ПВМП = 37 | |||||||||||||
| А | Б | В | Г | ||||
| 0 5 | 5 8 | 8 17 | 17 23 | ||||
| II | |||||||
| 10 14 | 14 17 | 17 23 | 23 27 | ||||
| IV | |||||||
| 27 + 5 + 3 = 35 | |||||||
| ПВМП = 35 | |||||||
Рис. 23. Промежуточные (условные) матрицы.
Конечные (реальные) матрицы
| ОФР | А | Б | В | Г | ОФР | А | Б | В | Г | |
| II | 0 5 | 5 8 | 8 17 | 17 23 | II | 0 5 | 5 8 | 8 17 | 17 23 | |
| IV | 10 14 | 14 17 | 17 23 | 23 27 | IV | 10 14 | 14 17 | 17 23 | 23 27 | |
| I | 17 21 | 21 23 | 23 30 | 30 35 | III | 23 31 | 31 34 | |||
| 25 28 | 28 30 | 30 38 | 38 41 | 31 38 | 38 43 | |||||
| III | I |
Рис. 24. Конечные (реальные) матрицы.
Поскольку брошенные развитием матрицы имеют меньшее значение ПВМП, постольку необходимо продолжить их развитие, то есть осуществить построение соответствующих конечных (реальных) матриц.
Конечные (реальные) матрицы
| ОФР | А | Б | В | Г | ОФР | А | Б | В | Г | |
| IV | 0 4 | 4 7 | 7 13 | 13 17 | IV | 0 4 | 4 7 | 7 13 | 13 17 | |
| II | 5 10 | 10 13 | 13 22 | 22 28 | II | 5 10 | 10 13 | 13 22 | 22 28 | |
| I | 16 20 | 20 22 | 22 29 | 29 34 | III | 17 20 | 20 22 | 22 30 | 30 33 | |
| 29 37 | 37 40 | 24 28 | 28 30 | 30 37 | 37 42 | |||||
| III | I |
| ОФР | А | Б | В | Г | ОФР | А | Б | В | Г | |
| II | 0 5 | 5 8 | 8 17 | 17 23 | II | 0 5 | 5 8 | 8 17 | 17 23 | |
| III | 17 25 | 25 28 | III | 12 15 | 15 17 | 17 25 | 25 28 | |||
| I | 25 32 | 32 37 | IV | 18 22 | 22 25 | 25 31 | 31 35 | |||
| 32 38 | 38 42 | 25 29 | 29 31 | 31 38 | 38 43 | |||||
| IV | I |
| ОФР | А | Б | В | Г | ОФР | А | Б | В | Г | |
| III | 0 3 | 3 5 | 5 13 | 13 16 | III | 0 3 | 3 5 | 5 13 | 13 16 | |
| II | 5 10 | 10 13 | 13 22 | 22 28 | II | 5 10 | 10 13 | 13 22 | 22 28 | |
| I | 16 20 | 20 22 | 22 29 | 29 34 | IV | 15 19 | 19 22 | 22 28 | 28 32 | |
| 22 26 | 26 29 | 29 35 | 35 39 | 22 26 | 26 28 | 28 35 | 35 40 | |||
| IV | I |
| ОФР | А | Б | В | Г | ОФР | А | Б | В | Г | |
| II | 0 5 | 5 8 | 8 17 | 17 23 | II | 0 5 | 5 8 | 8 17 | 17 23 | |
| I | 17 24 | 24 29 | I | 11 15 | 15 17 | 17 24 | 24 29 | |||
| III | 24 32 | 32 35 | IV | 17 21 | 21 24 | 24 30 | 30 34 | |||
| 32 38 | 38 42 | 25 28 | 28 30 | 30 38 | 38 41 | |||||
| IV | III |
Рис. 25. Конечные (реальные) матрицы.
Рассмотрение результатов оптимизации потока с НОФ показывает, что оптимальными очередностями являются I, IV, II, III; I, II, IV, III; III, I, II, IV; III, II, I, IV; которым соответствует минимальная продолжительность потока равная 39 ед. времени.
Данный алгоритм строг (математически доказан), но применительно к принятым условиям он оказался весьма трудоемок. Алгоритм потребовал формирования и расчета 16 промежуточных (условных) матриц и 24 конечных (реальных), то есть приведенный объем работы превышает объем, соответствующий полному перебору. Это редкий случай, но поскольку в определенных условиях он имеет место, постольку возникает задача разработки менее трудоемкого алгоритма.
Эта задача была решена кубинскими студентами В.Л.Агиляром и Б.Д.Меной, разрабатывавшими дипломные проекты под руководством лектора. Ими предложен эвристический (то есть не строгий) алгоритм, но он обеспечивает существенное уменьшение трудоемкости расчета.
Сущность алгоритма Агиляра и Мены заключается в выяснении периодов смещения (развертывания) каждого последующего фронтального комплекса относительно предшествующего во всех возможных сочетаниях фронтальных комплексов. Затем формируются варианты объектных потоков путем установки на первое место поочередно всех фронтальных комплексов, а на последующие – те, у которых наименьшая величина смещения (развертывания).
Проиллюстрируем работу данного алгоритма на примере расчета, начиная с представления исходных данных в виде независимо сформированных фронтальных комплексов и выявления расчетных (максимальных) смещений между парами фронтальных комплексов, сведенными в матрицы смежности.
| ОФР | А | Б | В | Г | max TP | МС | последующие ФР.К. | ||||
| I | II | III | IV | ||||||||
| I | 0 4 | 4 6 | 6 13 | 13 18 | предшествующие ФР.К. | I | |||||
| TP | |||||||||||
| 0 5 | 5 8 | 8 17 | 17 23 | II | |||||||
| II | |||||||||||
| TP | |||||||||||
| 0 3 | 3 5 | 5 13 | 13 16 | III | |||||||
| III | |||||||||||
| TP | |||||||||||
| 0 4 | 4 7 | 7 13 | 13 17 | ||||||||
| IV | IV | ||||||||||
Рис. 26. Результаты формирования вариантов потока с НОФ и определения продолжительности, как суммы величин смещений (развертывания) фронтальных комплексов и продолжительности последнего в очереди фронтального комплекса.
| № п/п | Формируемые очередности | Продолжительности потока с НОФ |
| 1. | I, II, IV, III | 5 + 10 + 8 + 16 = 39 |
| 2. | II, IV, I, III | 10 + 7 + 8 + 16 = 41 |
| 3. | III, II, IV, I | 5 + 10 + 7 + 18 = 40 |
| 4. | IV, II, I, III | 5 + 11 + 8 + 16 = 40 |
Рис. 27. Результаты оптимизации потока с НОФ по методике Агиляра и Мены.
Таким образом, алгоритм позволил в данном случае выявит только одну оптимальную очередность освоения фронтов работ, но это достигнуто при существенно меньшей трудоемкости расчетных операций.
Еще более компактный, но также эвристический алгоритм поиска оптимальных очередностей освоения фронтов в потоке с НОФ предложил А.В.Афанасьев.
Сущность алгоритма А.В.Афанасьева сводится к выявлению продолжительности самого продолжительного вида работ и размещения на первом и последнем местах в объектном потоке фронтальных комплексов с минимальной продолжительностью предшествующих последующих работ. При этом промежуточные фронтальные комплексы размещаются во всех возможных очередностях. Разумеется, что выявленные таким образом оптимальные очередности нуждаются в расчетной проверке путем построения и расчета конечных реальных матриц.
Проиллюстрируем методику поиска оптимальных очередностей освоения фронтов на примере с теми же исходными данными.
Рассмотрение продолжительностей видов работ показывает, что минимальная продолжительность у вида работ «В». В качестве минимальных по продолжительности предшествующих и последующих работ могут выступать работы «А» и «Б» первого фронтального комплекса и работа «Г» третьего фронтального комплекса (Σ =4 + 2 + 3 = 9)
I, … , III; T = 4 + 2 + 30 + 3 = 39;
III, … , IV; T = 3 + 2 + 30 + 4 = 39
При этом возможно формирование вариантов организации работ:
I, II, IV, III и I, IV, II, III;
III, I, II, IV и III, II, I, IV.
Расчет этих вариантов организации работ (см. выше) показывает, что все они дают минимальную продолжительность, то есть очередности являются оптимальными.
ЛЕКЦИЯ №6
Дата добавления: 2015-12-08; просмотров: 925;
