Методы обработки экспертной информации

Существуют три вида методов обработки:

– статистические методы;

– алгебраические методы;

– методы шкалирования.

Рассмотрим статистические методы экспертных оценок.

Результаты оценок каждого эксперта можно рассматривать как реализацию некоторой случайной величины из Ωэ и применять к ним методы математической статистики. Статистические методы позволяют определить согласованность мнений экспертов, значимость полученных оценок и т.д., то есть качество экспертизы.

Численные оценки. Экспертиза Э1.

Задача состоит в сопоставлении оцениваемой альтернативе (системе) одного числа.

(Ω=E1, Ωэ=E1, L – эксперты изолированы; Q – обратная связь отсутствует)

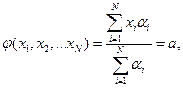
где αi – вес (коэффициент компетентности) экспертов;

xi – числовые оценки экспертов.

При отсутствии информации о компетентности экспертов αi=1. Степенью согласованности мнений экспертов служит дисперсия:

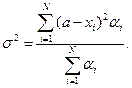
Другая экспертиза Э2 повышает точность оценивания (Ωэ=Е3)

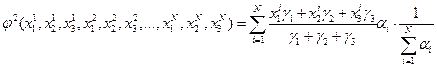
где 1 2 3 xi , xi , xi – оптимистическая, наиболее вероятная, и пессимистическая оценки i-ого эксперта.

γ1,γ2,γ3 – определяются эмпирически (например, по одной методике γ1=1, γ2=4, γ3=36, по другой γ1=3, γ2=0, γ3=2, γ4=25, где γ4 – степень неуверенности эксперта в своем ответе, γ1>γ3 , так как человек склонен к занижению оценки).

Степень согласованности экспертов определяется дисперсией

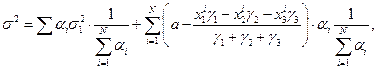
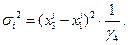
В экспертизах Э1 и Э2 можно определить статистическую значимость полученных результатов. Задавшись Рош , укажем интервал, в который оцениваемая величина попадет с вероятностью 1-Рош.

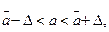
а - распределена нормально с центром ā и дисперсией (10.2).

Тогда

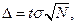
где t – стандартная ошибка, находящаяся по таблице распределения коэффициента Стьюдента t = f(N-1, Рош).

Пример. Десять экспертов с одинаковыми весами αi=1 оценивают величину Т. От них получены результаты:

Т1=33 Т2=35 Т3=32,2 T4=34 T5=38

T6=34 T7=37 T8=40 T9=36 T10=35.5

По формуле (10.1) получаем Т=35,5, 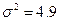σ=2.2136.

Задав Рош=0,05, определим t=f(9;0.005)=2,262. По формуле (10.5) Δ=1,583. Таким образом, с вероятностью 0,95 величина Т находится в интервале [33,917; 37,083].