Многоэтапное принятие решений

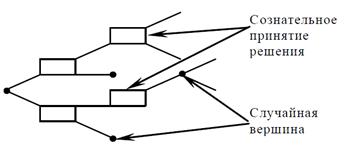
Рис. 1

Мы рассмотрели различные критерии принятия решений в условиях неопределённости. На практике, в таких задачах как проектирование изделий, управление процессами, создание сложных программных комплексов, мы можем столкнуться с принятием последовательных решений (цепочкой решений).

Особое значение такие многоэтапные решения имеют при создании автоматизированных экспертных систем. Рассмотрим вопрос оптимизации многоэтапных решений. Многоэтапность приводит к тому, что схема принятия решения может быть представлена в виде дерева, в каждой вершине которого осуществляется:

1) Сознательный выбор между двумя и более альтернативами

2) Либо случайный переход из одной ветви в другую под воздействием внешних случайных факторов.

Рассмотрим пример оптимизации многоэтапных решений на примере экономической задачи.

Пример. Фирма может принять решение о строительстве крупного или мелкого предприятия. Строительство крупного предприятия относительно дешевле, в случае если будет высокий спрос на производимые товары, мелкое предприятие можно расширить. Деятельность фирмы рассматривается в течение десяти лет, причём в случае строительства мелкого предприятия вопрос о расширении будет рассматриваться через два года. Спрос заранее неизвестен.

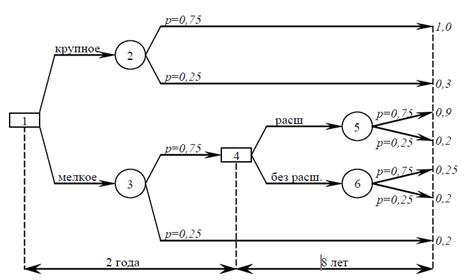
Рис. 2

Введём градацию случайного спроса: высокий (p>0,75) и низкий (p<0,25). Затраты и доходы: строительство крупного предприятия - 5 млн. $; строительство мелкого - 1 млн. $; затраты на расширение - 4,2 млн. $; крупное предприятие при высоком спросе даёт доход - 1 млн. $ ежегодно, а при низком - 300 тыс. $; мелкое предприятие при высоком спросе - 250 тыс. $ ежегодно, при низком - 200 тыс. $; расширенное предприятие в случае высокого спроса приносит доход - 900 тыс. $ в год, и при низком спросе - 200 тыс. $; мелкое предприятие без расширения при высоком спросе на производимый продукт приносит в течение двух лет по 250 тыс. $ ежегодно, а в течение следующих восьми по 200 тыс. $. Нарисуем дерево решений.

Применим для решения этой задачи метод динамического программирования. В качестве критерия применим средний выигрыш, т. е. МО выигрыша. Сама величина критерия равна доходу без затрат на строительство. Начнём с последнего четвёртого шага, подсчитаем средний выигрыш:

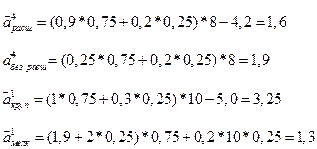
Исходя из полученного результата, оптимальным будет сразу строить крупное предприятие.

Другим примером оптимизации многоэтапных операций является известная «задача о секретарше».

Директор собирается принять на работу секретаршу. Прежний опыт делит секретарш на три категории: отличных (3 балла), хороших (2 балла) и посредственных (1 балл). Анализ учебных заведений по подготовке секретарш даёт статистику выпускниц заведений: вероятность взять на работу отличную секретаршу - 0,2, хорошую - 0,5, посредственную - 0,3. директор может испытать только трёх претенденток, причём в случае отказа директора кандидат убывает на другую работу. Построим дерево решений.

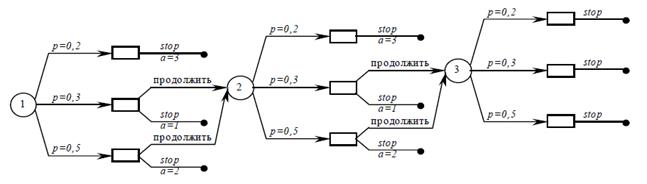
Рис. 3

В соответствии с процедурой динамического программирования начнём искать оптимальное решение с последнего шага. Определим математическое ожидание «выигрыша», если мы испытываем третьего кандидата:

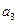=3*0,2+2*0,5+1*0,3=1,9 .

Далее определим средний выигрыш, если мы испытываем второго и третьего, с учетом того, что если второй будет посредственный, то мы продолжим и получим в среднем 1.9.

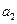=3*0,2+2*0,5+1,9*0,3=2,17 .

Поэтому если во втором испытании попалась хорошая секретарша, надо остановиться, т.к. получим 2, а если продолжим, то только 1.9.

При первом испытании, надо остановиться, только если попалась отличная, а в третьем испытании берём любую. Найдём средний оптимальный выигрыш при оптимальном правиле испытания трех кандидатов:

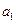=3*0,2+2,17*0,5+2,17*0,3=2,336 .