Решение игр в смешанных стратегиях
Если в игре верхняя и нижняя цена не совпадают ( a не равно b ), то зна-
чит, что седловой точки нет, но можно улучшить средний выигрыш игроков
А и В путем смешивания их стратегий. Это значит, что игрок А, каждый раз
играя игру, чередует свои чистые стратегии A1A2 ..........Am . Вопрос состоит
в том, какова должна быть доля случаев применения стратегий игроков.
Назовем смешанной стратегией игрока А вектор ( ) SA = p1 , p2 ,K, pm , в
котором показаны вероятности применения соответствующих стратегий. На-
пример: SA (0,1; 0,2; 0,7; 0) = , p 1
m
i 1
i = Σ=
- свойство полноты.__ Аналогично для игрока В получаем: SB = (q1 , q2 ,K,qm ), 1
q
n
i
j Σ =
=
.
Заметим, что чистая стратегия – это частный случай смешанной страте-
гии. A3 SA (0, 0,1, 0) = = .
Справедлива основная теорема теории игр: любая матричная игра имеет
решение в виде пары смешанных стратегий игроков А и В ( * )
B
*
SA ;S , дающих
оптимальное значение цены игры V*. Это оптимальное решение обладает
следующим свойством: если один игрок придерживается своей оптимальной
стратегии, то другому невыгодно отклоняться от своей оптимальной страте-
гии.
8.4. Упрощение игр и аналитическое решение игр 2×2
Прежде чем решать игру, ее необходимо упростить, т. е. если для игры
построена платежная матрица, можно вычеркнуть заведомо невыгодные
стратегии для игроков А и В.
Таблица 45
Здесь A2 уступает по всем компонентам A1, а B1 уступает и B2, и B3. За-
метим, что строки лучше, если элементы больше, а столбцы лучше, если
элементы меньше.
Если по каждой компоненте стратегии одна строка хуже другой, то ее
можно вычеркнуть. При этом решение игры упрощается.
В результате остаются такие строки и столбцы, которые нельзя сравнить.
Если число оставшихся стратегий хотя бы одного игрока равно двум, то игру
можно решить аналитически или геометрически.
Рассмотрим игры, в которых у каждого игрока лишь две стратегии. Если
в такой игре нет седловой точки, то значит, что все стратегии активны, т. е.
они войдут в решение с какой-то вероятностью, не равной нулю.
Справедлива теорема об активных стратегиях: если один из игроков при-
держивается своей оптимальной смешанной стратегии, то выигрыш остается
неизменным и равен цене игры V независимо от того, что делает другой иг-
рок, если только тот не выходит за пределы своих ак
Это чрезвычайно развитая область в экономике, в военном деле, в области обработки информации на фоне шумов и т. д. Рассмотрим элементы этой теории как продолжение теории игр.
Существуют задачи, в которых B - «бессознательный игрок», который мешает нам принимать правильные решения, но он не противодействует активно, а действует в соответствии с природными случайными явлениями, поэтому такую ситуацию называют игрой с природой. Например, помехи в канале связи для передачи информации, шумы при записи или воспроизведении звука и т. д. Ясно что бессознательное воздействие в целом вредит нам меньше, чем сознательное. С другой стороны эта «бессознательность» приводит к непредсказуемому поведению операции. Можно считать ,что как и в теории игр мы боремся с противником, который не осознанно мешает нам. Например, это погодные условия, или случайный спрос при продаже товара. Вот почему в теории статистических решений, главной проблемой является обоснование принципов оценки различных ситуаций со стороны A. Заметим, что в теории игр был один принцип – принцип минимакса.
Таблица 1
| P1 | P2 | Pn | |||
| A1 | a11 | a12 | a1n | ||
| A2 | a21 | a22 | a2n | ||
| Am | am1 | am2 | amn |
Мы будем рассматривать дискретные альтернативы (стратегии) природы. Тогда, если у A имеется m стратегий, а у «природы» имеется n альтернатив, то может быть получена матрица выигрышей, при применении каждой пары Ai Pj.
Условия Pj иногда называются гипотезами. Если платежная матрица построена, то задача состоит в анализе матрицы с целью получить стратегию Ai, которая наиболее выгодна по отношению к другим. В простейшем случае, если какие-то строки матрицы заведомо невыгодны, то их можно отбросить и оставить только одну, безусловно лучшую. Столбцы платёжной матрицы нельзя отбрасывать, т. к. условия «природы» могут быть и в нашу пользу. При анализе платёжной матрицы можно сделать неверный вывод о качестве
нашего решения.
Пусть сравниваются два выигрыша, находящихся в разных столбцах aij и akl, причём j≠l. Если aij>akl, то вроде бы решение в i- строке лучше, чем решение в k- строке, но так просто можно сравнивать, если выигрыш соответствует одинаковым условиям.
Пример: Пусть в Томской области, приняв определенные управляющие решения, получили урожайность пшеницы 20 центнеров с гектара, а в Краснодарском крае - 25. Эти значения сравнивать нельзя, т. к. для Томской области это может быть рекордный (наилучший) результат, а для Краснодарского края – плохой, т.к. рекорд 50 . Решение нужно сравнивать с потенциальными возможностями.
Вот почему необходимо преобразовывать платёжную матрицу таким образом, чтобы каждый наш выигрыш соотносился с тем максимумом, который можно достигнуть в данных условиях Pj Для каждого Pj можно найти максимальную величину βj и вычислить величину rij = βj - aij называемую риском. Здесь
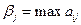
Чем риск меньше, тем лучше.
Дата добавления: 2015-11-06; просмотров: 811;
