Принятие решений при известных априорных вероятностях
Будем обозначать вероятности гипотез: Q1=p(P1), Q2=p(P2), …, Qn=p(Pn). Таким образом, мы считаем, что вероятности известны до того, как мы решили принять решение. Решение - выбор оптимальной стратегии A. Говорят, что это ситуация идеального наблюдателя.
Естественно, в качестве критерия выбирается средний выигрыш, который мы получим, если выберем стратегию Ai :
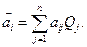
Это аналог математического ожидания. Решение принимается по критерию: 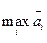 .
.
Это критерий максимального среднего выигрыша. Если задана матрица рисков, то можно для каждой строки вычислить средний риск:
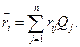
и оптимальным будет являться решение, которое обеспечивает величину: 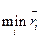
Покажем, что оптимальное решение можно искать как по (9.1), так и по (9.2). Сложим средний выигрыш и средний риск получим константу
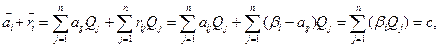
тогда
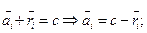
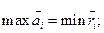
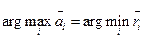
С – величина, не зависящая от i, это постоянная величина для данной строки.
В результате решения выбирается чистая стратегия ai. Есть ли смысл смешивать стратегии? Пусть мы смешиваем наши стратегии с вероятностями pi, тогда в результате применения смешанной стратегии мы получим средний выигрыш в таком виде:
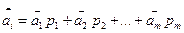 - математическое ожидание (МО).
- математическое ожидание (МО).
Мы знаем, что МО меньше максимального значения, следовательно в игре с природой нет смысла смешивать стратегии; чистая стратегия обеспечивает наилучший результат. Слабым местом в этом подходе является то, что надо знать априорные вероятности. Если они неизвестны, то необходимо их изучить. Это можно делать путём экспериментов, которые изучают условия «природы». Говорят, что этим мы обучаем нашу систему. Такой подход называется принципом адаптации к условиям.
Если априорные вероятности изучить не удаётся, то применяется принцип недостаточности основания: если не знаем о вероятности, то считаем, что гипотезы природы равновероятны. После этого применяем критерий идеального наблюдателя. Так как при равных вероятностях энтропия (неопределённость) максимальна, то мы рассчитываем на худший случай, т.е.применяем принцип пессимизма. Если сами значения вероятности неизвестны, но есть информация о предпочтениях гипотез, то существуют методы обработки предпочтений и получения вероятностей.
Если вероятности гипотез относятся как
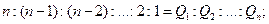
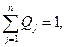
то можно подсчитать саму величину вероятности в следующем виде:
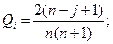
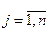
В некоторых случаях учитывается не только средний выигрыш, но также и дисперсия, т. е. величина разброса выигрыша в каждой строке:
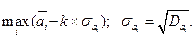
Дата добавления: 2015-11-06; просмотров: 745;
