Последовательность. Предел последовательности.
Числовой последовательностью называют бесконечное упорядоченное множество чисел (перенумерованное множество чисел).
Задают числовую последовательность с помощью общего члена xn.
{xn} - числовая последовательность с общим членом xn.
Например: {xn}={2;3;4;5;…}, xn=n+1;
{an}={1;1/2;1/3;…}, an=1/n ;
{bn}={-1;1;-1;1,…}, bn=(-1)n.
1) Определение (на языке ε): Число a называют пределом числовой последовательности {xn}, при n стремящемся к бесконечности (n®¥), если для любого, сколь угодно малого, положительного числа e, найдется номер последовательности N, зависящий от 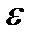 , начиная с которого выполняется неравенство |xn–a|<e.
, начиная с которого выполняется неравенство |xn–a|<e.
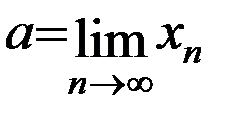 Û" e>0 $ N(
Û" e>0 $ N( 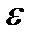 ): " n>N, выполняется |xn–a|<e.
): " n>N, выполняется |xn–a|<e.
(a-e; a+e) ‒ e-окрестность точки a.
2) Определение (на языке окрестности): Число a называется пределом последовательности {xn} при n®¥, если для любого сколь угодно малого положительного числа e, найдется такой номер последовательности N, начиная с которого члены последовательности будут находится в e- окрестности точки a.
Пример: Покажем по определению, что пределом числовой последовательности {xn} с общим членом xn= 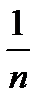 , является число a=0, то есть
, является число a=0, то есть 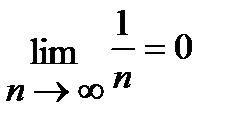 .
.
Возьмем сколь угодно малое положительное e. Попробуем найти такой номер последовательности N, начиная с которого выполняется неравенство
| 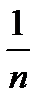 – 0|<e. " e>0 $ N: "n>N выполняется |
– 0|<e. " e>0 $ N: "n>N выполняется | 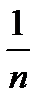 - 0|<e. Снимаем модуль
- 0|<e. Снимаем модуль 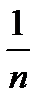 –0<e. Если перевернуть обе части неравенства, то перевернем знак: n>
–0<e. Если перевернуть обе части неравенства, то перевернем знак: n> 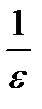 . В качестве N берется целая часть
. В качестве N берется целая часть 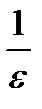 : N=[
: N=[ 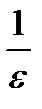 ].
].
3) 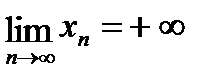 , если "A>0 $N: "n>N выполняется xn>A.
, если "A>0 $N: "n>N выполняется xn>A.
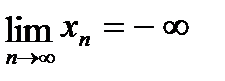 , если "A<0 $N: "n>N выполняется xn<A.
, если "A<0 $N: "n>N выполняется xn<A.
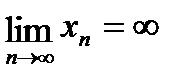 , если "A>0 $N: "n>N выполняется |xn| > A.
, если "A>0 $N: "n>N выполняется |xn| > A.
Дата добавления: 2015-11-06; просмотров: 711;
