Свойства сходящихся последовательностей.
1. Единственность.
Теорема: Сходящаяся последовательность имеет только один предел.
2. Арифметические действия.
Теорема: Если последовательности {xn} и {yn} сходящиеся, причем 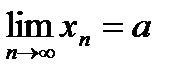 и
и 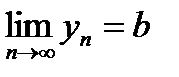 , тогда
, тогда 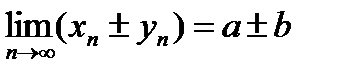 ;
; 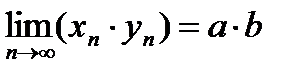 ;
; 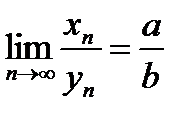 при условии
при условии 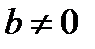 .
.
3. Необходимое условие сходимости.
Теорема Больцано-Вейерштрасса:
Сходящаяся последовательность ограничена.
Док-во:
Пусть последовательность {хn} сходится Þ существует конечный предел 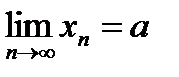 Þ по определению: для "e > 0 $ номер N, начиная с которого
Þ по определению: для "e > 0 $ номер N, начиная с которого 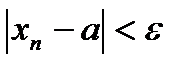 .
.
Из неравенства: 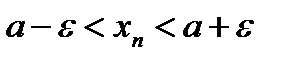 .
.
Выберем С=max { 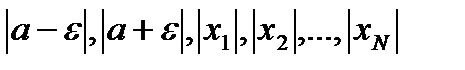 }.
}.
Значит, для членов последовательности {xn} выполняется неравенство 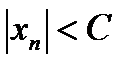 . Тогда по определению последовательность {xn} ограничена.
. Тогда по определению последовательность {xn} ограничена.
Ч.т.д.
4. Достаточные условия существования предела.
Определение: Последовательность {xn} называется возрастающей (неубывающей), если x1<x2<… (x1£x2£…).
Пример: 1<2<3<4<…, {xn} – возрастает.
1£1<2£2<3£3…, {xn} - неубывающая.
Определение: Последовательность {xn} называется убывающей (невозрастающей), если x1>x2>… (x1³x2³…).
Пример: 1>1/2>1/4>…, {xn} – убывающая.
1³1/2³1/2>1/3³1/3>…, {xn} - невозрастает.
Теорема1: Если последовательность монотонно возрастает и ограничена сверху, то она имеет конечный предел.
Теорема2: Если последовательность монотонно убывает и ограничена снизу, то она имеет конечный предел.
Док-во:
Докажем теорему 1.
{xn} возрастет Þ x1<x2<….
{xn} ограничена сверху Þ существует число М такое, что при "n xn 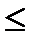 М. Отступим от М на e, тогда существует номер N, начиная с которого
М. Отступим от М на e, тогда существует номер N, начиная с которого
М-e< xn 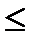 М.
М.
xn
М
М-e
0 1 2 3 4 n
Усилим правую часть неравенства:
М-e< xn<М+e, т.е. 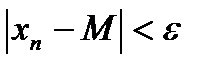 .
.
Значит, для "e > 0 $ номер N, начиная с которого справедливо
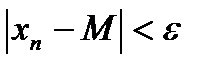 . Þ
. Þ 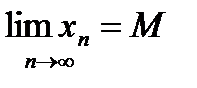 . Þ по определению: {xn} сходится.
. Þ по определению: {xn} сходится.
Теорема 2 доказывается аналогично.
Ч.т.д.
Предел функции.
Пусть функция y=f(x) определена в некоторой окрестности точки a, за исключением, может быть самой точки.
1) Определение предела функции на языке 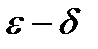 :
:
Число А называется пределом функции f(x) при x®a, если для любого сколь угодно малого положительного числа e найдется число d(e)>0 такое, что для всех x, отличных от a и удовлетворяющих неравенству |x-a|<d, следует неравенство |f(x)-A|<e.
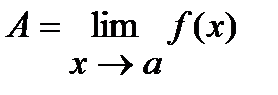 Þ "e>0 $d>0: из |x-a|<d Þ |f(x)-А|<e.
Þ "e>0 $d>0: из |x-a|<d Þ |f(x)-А|<e.
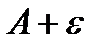
| y |
A
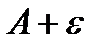
| х |
   |
Интервал (a-d, a+d) на оси ОХ называется дельта-окрестностью точки a.
Интервал (A-e, A+e) на оси ОY называется эпсилон-окрестностью точки A.
Функция y=f(x) переводит каждую точку из d-окрестности точки a на оси ОХ внутрь ε-окресности точки А на оси ОY.
2) Определение предела на языке окрестности:
Число A называется пределом функции при x®a, если для любой сколь угодно малой e-окрестности точки A на оси ОY найдется d-окрестность точки a на оси ОХ, которую функция переводит в e-окрестность.
3) Определение предела на языке последовательности:
Число A называется пределом функции f(x) при x®a, если для любой последовательности {xn}, сходящейся к точке a, соответствующая последовательность значений функции {f(xn)} сходится к A.
4) Правый и левый пределы.
Определение: Если есть xn®a и xn<a, то число A называется левым пределом функции при x®a-0.
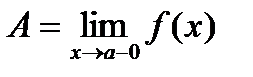 .
.
Определение: Если xn®a и xn>a, то число A называют правым пределом функции при x®a+0.
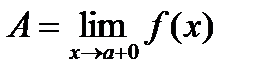 .
.
Такие пределы называются односторонние.
Замечание 1: Для существования предела функции не требуется, чтобы функция была определена в самой точке x=a, достаточно того, что она определена в ее окрестности.
Замечание 2: На последовательность {xn} можно смотреть как на функцию натурального аргумента xn=f(n), nÎN. Поэтому все свойства пределов и теоремы для пределов функции справедливы и для предела последовательности.
Дата добавления: 2015-11-06; просмотров: 1255;
