Основные характеристики функции.

Понятие функции, способы задания функции.

Определение: Если каждому элементу множества D поставлен в соответствие единственный элемент множества E, то говорят, что задана однозначная функция действующая из D в E.

D – область определения функции. E – множество значений функции.

xÎD – аргумент функции, yÎE – значение функции.

Способы задания функции:

1) Описание.

2) Табличный.

3) Графический.

Определение: Графиком функции y=f(x) называется множество точек плоскости с координатами (x,f(x)), где xÎD(f).

4) Аналитический.

С помощью формулы y=f(x). Например: y=sin x+x², y=2x³.

Область определения функции D(f) или D(y) – это множество тех значений аргумента x, при которых формула, задающая функцию, имеет смысл.

Основные характеристики функции.

1. Возрастающие и убывающие функции.

Функция y=f(x) называется возрастающей на (а;b), если большему значению аргумента соответствует большее значение функции, т.е. "x1<x2 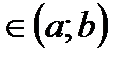выполняется f(x1)< f(x2).	x2 x1   х x1
Функция y=f(x) называется убывающей на (а;b), если большему значению аргумента, соответствует меньшее значение функции, т.е. "x1<x2 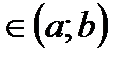выполняется f(x1)>f(x2).	x2 x1

Возрастающие и убывающие функции на (а;b) называются монотонными на этом интервале.

2. Четные, нечетные и периодические функции.

Функция y=f(x) называется нечетной, если область определения функции D(y) симметрична относительно точки О(0;0) и y(-x)=-y(x).

График нечетной функции имеет симметрию относительно точки О(0;0). Пример: y=x³.

Функция y=f(x) называется четной, если область определения D(y) симметрична относительно точки О(0;0) и y(-x)=y(x).

График четной функции имеет симметрию относительно оси Оy.

Пример: y=x².

Функции, не являющиеся четными или нечетными, называются функциями общего вида.

Пример: y=x²+x+1 или y=x+2.

Функция y=f(x) называется периодической с наименьшим положительным периодом T, если f(x+T)=f(x).

Пример: sin(x+2p)=sin x, где T=2p;

cos(x+2p)=cosx, где T=2p;

tg(x+p)=tgx, T=p;

ctg(x+p)=ctg x, T=p.

Уравнение F(x,y)=0 задает y как неявную функцию от x.

Пример: e^y +x =0 ‒ неявное задание функции.

x²y³+cos(xy⁴)=0 – неявное задание функции.

y=x³+1/x – явное задание функции.

3. Сложная и обратная функции.

Пусть функция y=f(x) действует из множества D во множество E (D®E), а функция x=x(t) действует из множества T во множество D (T®D), тогда сложная функция y=f(x(t)) действует из T в E.

Пример: y=sin(y²+1) - функция x(t)=t²+1, функция y(x)=sin x.

Пусть y=f(x) действует D®E, обратная функция x=j(y) действует из E®D.

Пример: y=2x –3. Выразим отсюда x: x=(y+3)/2, заменим x на y, а y на x y=(x+3)/2 – обратная функция.