Единственность предела функции.
Теорема: Если функция имеет предел при x®a, то он единственен.
Док-во: Предположим противное. Пусть у функции существуют два предела при x®a  и
и 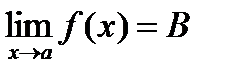 . Возьмем e>0 так, чтобы окрестности точек A и B не пересекались. По определению предела функции: существует такое d>0, что из |x-a|<d следует |f(x)-A|<e, |f(x)-B|<e, т.е. значения f(x) лежат одновременно в e-окрестности точки A и e-окрестности точки B, чего быть не может, т.к. окрестности не пересекаются, полученное противоречие доказывает теорему.
. Возьмем e>0 так, чтобы окрестности точек A и B не пересекались. По определению предела функции: существует такое d>0, что из |x-a|<d следует |f(x)-A|<e, |f(x)-B|<e, т.е. значения f(x) лежат одновременно в e-окрестности точки A и e-окрестности точки B, чего быть не может, т.к. окрестности не пересекаются, полученное противоречие доказывает теорему.
Ч.т.д.
Бесконечно малые и бесконечно большие функции.
Иx свойства.
Определение: Функция a(x) называется бесконечно малой при x®x0, если 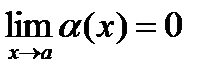 .
.
Обозначается a(x) – б/м при x®x0.
Функция a(x) – б/м при x®x0, если " 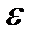 >0 $d>0: из |x-x0| <d Þ |a(х)|<
>0 $d>0: из |x-x0| <d Þ |a(х)|< 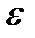 .
.
Определение: Функция y=f(x) называется ограниченной, если существует такое число M >0, что |f(x)| 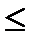 М при "
М при " 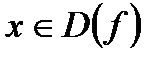 .
.
Определение: Функция f(x) называется бесконечно большой при x®x0, если 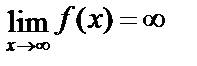 .
.
Обозначается f(x) — б/б при x®x0.
Функция f(x) — б/б при x®x0, если для любого А>0 найдется d>0: из неравенства |x-x0|<d следует неравенство |f(x)|>А.
В качестве x0 может быть конечное число, ±¥ или ¥.
Свойства.
1. Сумма двух или конечного числа б/м есть бесконечно малая.
2. Произведение двух или конечного числа б/м есть бесконечно малая.
3. Произведение б/м на ограниченную функцию есть б/м.
Замечание: Частное двух б/м является неопределенностью вида 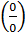 .
.
4. Сумма конечного числа б/б есть б/б.
5. Произведение конечного числа б/б есть б/б.
6. Произведение б/б на любую не б/м есть б/б.
Замечание: Разность двух б/б является неопределенностью вида (¥-¥).
Замечание: Частное двух б/б является неопределенностью вида 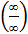 .
.
Замечание: Произведение б/б на б/м является неопределенностью вида  .
.
7. Частное от деления б/б на ограниченную функцию есть б/б.
8. Б/м и б/б ‒ взаимообратные функции.
Док-во:
1) б/м есть обратная величина для б/б. 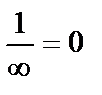 .
.
Пусть f(x) – б/б при x®x0. Тогда по определению б/б: для любого A>0 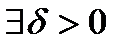 такое, что из неравенства |x-x0| <d будет следовать неравенство |f(x)| >A. Перейдем к обратным величинам: |1/f(x)| < 1/A Þ б/м по определению.
такое, что из неравенства |x-x0| <d будет следовать неравенство |f(x)| >A. Перейдем к обратным величинам: |1/f(x)| < 1/A Þ б/м по определению.
2) б/б есть обратная величина для б/м.
Пусть a(x) – б/м при x®x0. Тогда по определению: " 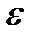 >0 $ d>0 такое, что из неравенства |x-x0|<d Þ неравенство |a(x)|<
>0 $ d>0 такое, что из неравенства |x-x0|<d Þ неравенство |a(x)|< 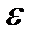 . Перейдем к обратным величинам: |1/a(x)| > 1/
. Перейдем к обратным величинам: |1/a(x)| > 1/ 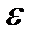 , что означает по определению, что 1/a(x) – б/б величина.
, что означает по определению, что 1/a(x) – б/б величина.
Ч.т.д.
Дата добавления: 2015-11-06; просмотров: 3782;
