Условно категорические умозаключения
Проанализируем те умозаключения, которые встретились в речи Сообразительного студента в ходе решения задачи.
(1) Если 1 наверху, то 2 в середине, и 1 наверху, следовательно, 2 в середине.
(2) Если 3 в середине, то 1 наверху, и 1 наверху, следовательно, 3 в середине.
Обозначим наши суждения так же, как обозначил их Студент-тугодум, но заменим символы p, q, r на метапеременные A, B, С.
Тогда логическую форму умозаключения (1) мы сможем записать в таком виде:
(1) А  В, А |- В,
В, А |- В,
а логическую форму умозаключения (2) в следующем виде:
(2) С  А, А |- С.
А, А |- С.
Напомню, что знак "|- " заменяет слово "выводимо".
Из нашего диалога выяснилось, что умозаключение (1) является правильным, а умозаключение (2) - неправильным. Попытаемся подтвердить это содержательно. Рассмотрим следующее умозаключение, совершенное одним следователем: "Если этот человек преступник, то он был на месте преступления. Этот человек был на месте преступления. Следовательно, этот человек преступник". Каждый из вас сразу же скажет, что это умозаключение неправильно. Действительно, из того, что некий человек был на месте преступления, нельзя с достоверностью заключить, был он преступником или нет. На месте преступления ведь были и свидетели, и, наконец, жертва. Но мы видим, что умозаключение нашего незадачливого следователя происходит по той же самой схеме, что и наше умозаключение (2). Действительно, обозначим суждение "Этот человек преступник" через p, "Этот человек был на месте преступления" через q. Тогда мы получим следующую схему:
p  q, q |- p.
q, q |- p.
Очевидно, что это - конкретизация схемы умозакйючения (2). Наш пример показывает, что (2) - это схема такого умозаключения, которое от истинных посылок может вести к ложному заключению, а значит, это умозаключение неправильно.
Решая эту задачу, мы столкнулись с одним из видов условно-категорических умозаключений. Дадим их общее определение.
Условно-категорическими называются умозаключения, в которых одна посылка - условное суждение, а вторая посылка и заключение - суждения категорические.
Терминология "условно-категорические" умозаключения - дань традиции. То, что здесь называется категорическим суждением, совпадает с традиционным понятием категорического суждения (т. е. включает в себя как утвердительные простые суждения, так и отрицательные простые суждения) и несколько отличается от тех простых суждений, которые мы изучали в теме "Суждение". Однако использования языка логики суждений для формализации таких умозаключения вносит некоторые изменения в наш подход к понятию категорического суждения в данном контексте. Говоря об умозаключениях логики суждений, мы под термином "категорическое суждение" всегда будем иметь в виду простые утвердительные суждения в смысле §1 главы 6 или их отрицания (т. е. любое суждение p и суждение 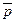 мы будем считать категорическим суждением[49]). До сих пор мы рассмотрели один вид условно-категорических умозаключений, схема которых выглядит так:
мы будем считать категорическим суждением[49]). До сих пор мы рассмотрели один вид условно-категорических умозаключений, схема которых выглядит так:
А  В, А |- В
В, А |- В
Умозаключения, совершаемые по схеме А  В, А |- В назовем умозаключениями от утверждения основания к утверждению следсрвия
В, А |- В назовем умозаключениями от утверждения основания к утверждению следсрвия
В классической традиции он еще называется латинским термином modus ponendo ponens или проще - modus ponens (что означает способ утверждающе утверждающий, или проще - способ утверждающий).
Вместе с тем запомним, что такой вид умозаключений, как
А  В, В |- А
В, В |- А
называемый: от утверждения следствия к утверждению основания, является неправильным.
Проверить правильность умозаключения от утверждения основания к утверждению следствия можно при помощи таблиц. Мы помним, что нам для этого следсет объединить посылки при помощи союза "и" и проверить, имеется ли отношение логического следования между получившимся сложным суждением и заключением.
| А | В | А  В В
| (А  В) В)  А А
| В |
| И И Л Л | И Л И Л | И Л И И | И Л Л Л | И Л И Л |
Мы видим, что в таблице нет такого случая, когда первое суждение истинно, а второе ложно, следовательно, между ними имеется отношение логического следования и наше умозаключение правильно.
Умозаключения от утверждения основания к утверждению следствия являются весьма простыми и на примерах выглядят тривиально. Рассмотрим несколько примеров.
Пример. Если каждый день пить кофе, то рано или поздно в голову придет хорошая идея. Этот человек каждый день пьет кофе. Следовательно, ему рано или поздно в голову придет хорошая идея.
Пример. Если человек каждый день смотрит телевизор, то он становится глупее. Этот человек каждый день смотрит телевизор. Следовательно, он становится глупее.
Пояснение. По этой схеме вы сами можете придумать сколь угодно много примеров. Однако дело не в этих примерах. Существенен следующий вопрос: почему, несмотря на тривиальность этого вида умозаключений, логики им охотно пользуются, и во многих формализованных системах логики modus ponens является единственным правилом вывода? Дело в том, что умозаключения от утверждения следствия к утверждению основания являются хорошим средством поиска доказательства тех суждений, которые мы хотим обосновать. Они нам подсказывают, что для того, чтобы доказать суждение В, нужно найти друбое суждение А, которое не только было бы истинным, но и составленная из А и В импликация А  В также была бы истинной. В этом смысле modus ponens является составляющей частью закона достаточного основания. Действительно, чтобы доказать суждение В согласно рассматриваемому способу умозаключения, нужно найти другое суждение, которое было бы достаточным основанием истинности В. Однако изолированное суждение не может быть достаточным основанием. Чтобы получить А необходимо так связать суждения А и В, чтобы А было условием для В, а это и есть импликация А
В также была бы истинной. В этом смысле modus ponens является составляющей частью закона достаточного основания. Действительно, чтобы доказать суждение В согласно рассматриваемому способу умозаключения, нужно найти другое суждение, которое было бы достаточным основанием истинности В. Однако изолированное суждение не может быть достаточным основанием. Чтобы получить А необходимо так связать суждения А и В, чтобы А было условием для В, а это и есть импликация А  В.
В.
Допустим, нам надо доказать, что данное тело расширяется. Достаточным основанием для этого будет тот факт, что это тело нагревается. Но для того, чтобы полностью обосновать доказываемое утверждение, нам еще необходимо привести импликацию "Если тело нагревается, то оно расширяется". Обозначим суждение "Тело нагревается" через р, тело расширяется - через q. Тогда наш вывод будет выглядеть следующим образом:
p  q, p|- q.
q, p|- q.
В этом выводе нельзя не узнать частный случай нашего умозаключения "от утверждения основания к утверждению следствия".
Ав: Теперь, я думаю, вам не доставит труда справиться со следующей задачей: условия те же самые, что и в предыдущей задаче, только суждения несколько другие:
(а) Если 2 внизу, то 1 в середине.
(б) Если 1 в середине, то 3 внизу.
(в) 1 наверху.
Ст: Да, но здесь ничего не получается. Я заметил, что в предыдущем умозаключении у нас получался вывод, потому что в посылках было одно общее суждение. А здесь у нас общего суждения нет.
Сс: Значит, надо его сделать!
Ст: Как это “сделать”?
Сс: Ну, получить или еще что-нибудь там.
Ав: Попытайтесь!
Сс: Я думаю, мы можем сказать, что если 1 наверху, то 1 не в середине.
Ст: Ага, правильно! Теперь мы получили общее суждение.
Ав: Получить-то получили, а что дальше?
Сс: Дальше так. Из того, что 1 не в середине, и суждения (а) мы можем получить, что 2 не внизу, т.е. 2 в середине. А из того, что 1 не в середине, и суждения (б) - что 3 не внизу, р.е. 3 в середине.
Ст: У тебя опять получились два объекта в одном квадрате.
Сс: Теперь мы знаем, что делать. Это означает, что одно из умозаключений, которые я применил, правильное, а другое - нет. Осталось только решить, какое именно.
Ст: Давайте попробуем, как в прошлый раз. Обозначим суждение "2 внизу" через р, "1 в середине" - через q, "3 внизу" - через r . Тогда "1 не в середине" будет 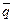 . Отсюда твое первое умозаключение будет выглядеть следующим образом:
. Отсюда твое первое умозаключение будет выглядеть следующим образом:
1) p  q,
q, 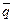 |-
|- 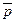 ,
,
2) q  r,
r, 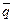 |-
|- 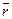 .
.
Теперь осталось составить таблицы. Сначала для первого умозаключения:
| P | q | p  q q
| 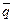
| (p  q) q)  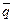
| 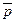
| |
| И И Л Л | И Л И Л | И Л И И | Л И Л И | Л Л Л И | Л Л И И |
Так, здесь есть отношение логического следования между (p  q)
q) 
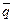 и
и 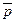 . Для второго умозаключения таблица будет выглядеть следующим образом:
. Для второго умозаключения таблица будет выглядеть следующим образом:
| q | r | q  r r
| 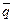
| (q  r) r)  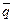
| 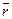
|
| И И Л Л | И Л И Л | И Л И И | Л Л И И | Л Л И Л | Л И Л И |
Здесь в третьей строке суждение (q  r)
r) 
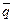 истинно, а суждение
истинно, а суждение 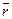 ложно. Значит, между этими суждениями нет отношения логического следования, а это означает, что второе умозаключение неправильно. Следовательно, 2 в середине, а 3 внизу.
ложно. Значит, между этими суждениями нет отношения логического следования, а это означает, что второе умозаключение неправильно. Следовательно, 2 в середине, а 3 внизу.
Ав: Что же у вас уже сформировался систематический метод проверки умозаключений.»
Таким образом, в диалоге наших героев мы встретились с двумя типами умозаключений. Приведем их общие схемы с метапеременными:
(1) А  В,
В, 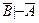 .
.
(2) А  В,
В, 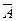 ├
├ 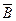
Из диалога нам стало ясно, что умозаключения по первой схеме правильные, а по второй - неправильные.
Покажем, что аторая схема неправильная, при помощи контрпримера, т.е. умозаключения, совершаемого по указанной форме, но в котором посылки явно истинны, а заключение может быть и ложным.
Контрпример. В качестве контрпримера рассмотрим умозаключение, которым часто пользуются врачи, когда решают выписать больничный лист или нет:
Если у человека повышена температура, то он болен.
У этого человека температура не повышена.
Следовательно, он не болен.
Мы видим, что в этом умозаключении, происходящим по схеме (2), посылки мобут быть истинными, а заключение ложным. Следовательно, это умозаключение неправильно.
Пример. Рассмотрим умозаключение по схеме (1). Однажды была сформулирована гипотеза о том, что известный персонаж российской истории Лжедмитрий 1 учился в коллеже иезуитов. Тогда же было сформулировано следующее умозаключение: Лжедмитрий 1 не был воспитанником иезуитов, потому что он плохо знал латынь.
Развернем это умозаключение в полную форму:
Если бы Лжедмитрий 1 был учеником иезуитов, то он хорошо знал бы латынь.
Неверно, что Лжедмитрий 1 хорошо знал латынь.
Следовательно, Лжедмитрий 1 не был учеником иезуитов.
Мы видим, что в данном случае наше умозаключение было использовано для опровержения выдвинутой гипотезы. В этом и заключается главная роль такого типа умозаключений в познании и общении.
Умозаключения, совершаемые по схеме А  В,
В, 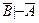 назовем умозаключениями от отрицания следствия к отрицанию основания.
назовем умозаключениями от отрицания следствия к отрицанию основания.
В традиции, идущей от средневековой логики, эти умозаключения назывались modus tollendo tollens, или проще modus tollens, что означает способ отрицающе-отрицающий или просто - способ отрицающий.
Умозаключения от отрицания следствия к отрицанию основания часто используются в аргументации и в ораторской практике.
Пример. Рассмотрим, каким образом использовал эти умозаключения знаменитый античный оратор Демосфен. В "Третьей речи против Филиппа" Демосфен говорил следующее: "... если кто-нибудь за мир считает такое положение, при котором тот человек [Филипп] получит возможность покорить всех остальных..., то он... не в своем уме". Очевидно, что Демосфен предполагает, что его слушатели считают, что они в своем уме. Отсюда следует заключение: "Нельзя считать за мир такое положение, при котором тот человек [Филипп] получит возможность покорить всех остальных". Ораторский эффект применения умозаключения от отрицания следствия ("мы в своем уме") к отрицанию основания ("нельзя считать...") заключается в том, что одна посылка и заключение остаются не высказанными, но столь очевидны, что любой слушатель получит необходимое заключение сам.
Схема этого рассуждения такова: обозначим суждение "Если кто-нибудь за мир считает... остальных" через p, суждение "Он в своем уме" - через q.
Тогда получается следующая схема:
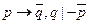 .
.
Нетрудно заметить, что это одна из модификаций нашего умозаключения от отрицания следствия к отрицанию основания. Только здесь, поскольку в консеквенте импликации стоит отрицательное суждение, его отрицание представлено суждением утвердительным.
Пример. В том же рексте Демосфена встречаем следующее рассуждение: "... если мы хотим дожидаться того времени, когда он сам признается, что ведет войну, тогда мы самые глупые люди...". Очевидно, что его слушатели не считают себя самыми глупыми людьми, а следовательно, они не должны дожидаться того времени, когда он сам признается, что ведет войну.
Обозначим
суждение "Мы хотим дожидаться того времени и т.д. "через p,
суждение "Мы самые глупые люди" - через q.
Тогда наше умозаключение будет выглядеть так:
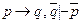
Это в точности совпадает с нашей схемой умозаключения от отрицания следствия к отрицанию основания.
Пример. Еще один более сложный случай применения этого рода умозаключений уже не в ораторской прозе, а в ученом трактате дает нам знаменитый "Князь" Никколо Макиавелли. Там мы встречаем следующее рассуждение: "Он [Чезаре Борджиа] превозмог бы любые трудности, если бы его не теснили с двух сторон враждебные армии или не донимала болезнь". Слово "бы" в консеквенте импликации означает, что это утверждение на самом деле не истинно, т.е. истинно его отрицание. Что же получается в таком случае?
Обозначим сложное суждение "Его не теснили с двух сторон враждебные армии или не донимала болезнь" через А, а суждение "Он превозмог любые трудности" - через В. Тогда наше рассуждение будет иметь следующую форму:
А  В,
В, 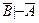
Таким образом, при помощи нашего умозаключения от отрицания следствия к отрицанию основания мы получаем следующее заключение: "Неверно, что его не теснили с двух сторон враждебные армии, и не донимала болезнь". Это последнее суждение само имеет форму 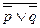 , что по законам логики суждений эквивалентно суждению
, что по законам логики суждений эквивалентно суждению 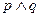 . Следовательно, окончательный вывод будет таков: "Его теснили с двух сторон враждебные армии и донимала болезнь". Таким образом, наши умозаключения позволили сформулировать точный вывод, который только предполагается в тексте Макиавелли, но не был сформулирован явным образом. Отсюда мы можем сделать общий вывод: знание умозаключений позволяет точно анализировать неявную информацию, содержащуюся в тексте.
. Следовательно, окончательный вывод будет таков: "Его теснили с двух сторон враждебные армии и донимала болезнь". Таким образом, наши умозаключения позволили сформулировать точный вывод, который только предполагается в тексте Макиавелли, но не был сформулирован явным образом. Отсюда мы можем сделать общий вывод: знание умозаключений позволяет точно анализировать неявную информацию, содержащуюся в тексте.
Дата добавления: 2015-11-04; просмотров: 1584;
