Тогда и только тогда, когда...» — эквивалентность — суждение эквивалентности.
Вы дали обещание: «Я пойду на лекцию по логике тогда и только тогда, когда поеду с тобой на море».
Отсюда получается следующая таблица:
| A | B | A 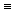 B B 
| |
| И | И | И | |
| И | Л | Л | |
| Л | И | Л | |
| Л | Л | И |
6. «Не...», «неверно, что...» — отрицание — отрицательные суждения.
Отрицание действует только на одно суждение, Поэтому таблица будет выглядеть следующим образом:
| A | 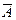
| |
| И | Л | |
| Л | И |
Мы выяснили смысл всех союзов, которые нас с вами интересовали, и поэтому можем вернуться к задаче, которую наши персонажи обсуждали в начале этого параграфа.
Ав: Как, теперь вам стал понятен смысл союза «или»?
Сс: Да, теперь можно решить задачу.
Ст: Каким образом?
Сс: Смотри. Начнем как всегда. Предположим, что X - лжец. Тогда все его суждение: «Я лжец, или Y — рыцарь» — ложно. Но теперь мы знаем, что разделительное суждение ложно только в том случае, когда оба составляющие его суждения ложны.
Ст: Как это ложны? Первое составляющее суждения «Я - лжец», раз мы предположили, что он лжец, должно быть истинным.
Сс: Вот, правильно! Ты мне подсказал, что делать дальше. Я пока доказал, что в предположении, что X - лжец, получается, что оба суждения, составляющие высказываемое им сложное суждение, ложны. Но поскольку он лжец, то первое из них, а именно «Я - лжец», должно быть в то же время истинным. Это означает, что мы встретили противоречие. Одно и то же суждение должно быть одновременно истинным и ложным. Так не бывает, по крайней мере, в логике. Значит, наше предположение неверно, X является рыцарем.
Ст: Здорово!
Сс: Дальше уже просто. Поскольку X - рыцарь, то все его суждение истинно. Но поскольку X — рыцарь, то первая составляющая этого сложного суждения - суждение «Я лжец» будет ложным. А из таблицы истинности мы знаем, что для того, чтобы суждение с «или» было истинным, необходимо, чтобы, по крайней мере, одно из составляющих его суждений было истинно. Поскольку же первое суждение ложно, то второму не остается ничего иного, как быть истинным. Значит, Y — рыцарь и оба они рыцари!
Ав: Поздравляю. Вы замечательно справились с задачей. А почему Вы с ней смогли справиться?
Сс: Потому что, благодаря таблице, я точно знал, что означает союз «или», и при решении задачи пользовался этим смыслом, зафиксированным в таблице.
Ав: Да, видите, получается, что мы не вполне понимали точный смысл обычных слов и это мешало нам рассуждать. Теперь же, когда мы понимаем точный смысл этих слов, препятствия устранены, и мы можем рассуждать свободно и, что еще более важно, правильно.
Однако выяснение смысла логических союзов — не единственное, в чем могут быть полезны таблицы истинности. Мы еще должны ответить на главный вопрос: каким образом истинность или ложность сложных суждений зависит от истинности или ложности входящих в них суждений? Для этого нам нужно научиться строить таблицы истинности для произвольных сложных суждений.
Введем необходимые вспомогательные понятия.
В суждении 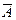 будем считать, что A является областью действия отрицания.
будем считать, что A является областью действия отрицания.
В суждениях А  В, А
В, А 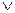 В, А
В, А 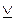 В, А®В, А
В, А®В, А 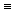 В будем считать суждения A и B областью действия соответствующего логического союза.
В будем считать суждения A и B областью действия соответствующего логического союза.
Простые утвердительные суждения, обозначаемые при помощи переменных ЯЛС, назовем суждениями степени 0 (ноль).
Если суждение C имеет вид  или А
или А  В, А
В, А 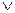 В, А
В, А 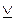 В, А®В, А
В, А®В, А 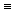 В, и если суждение A является суждением степени n, или если максимальная степень суждений А, B есть n, то суждение C является суждением степени n+1.
В, и если суждение A является суждением степени n, или если максимальная степень суждений А, B есть n, то суждение C является суждением степени n+1.
Пример. Суждение ( 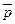
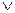 r)®s имеет степень 3, потому что суждение
r)®s имеет степень 3, потому что суждение 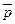 имеет степень 1, суждение
имеет степень 1, суждение 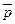
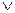 r имеет степень 2, а все суждение, следовательно, будет иметь срепень 3.
r имеет степень 2, а все суждение, следовательно, будет иметь срепень 3.
Пусть суждение C, истинность или ложность которого мы хотим установить, имеет степень m.
Тогда таблица строится следующим образом:
1. На входе выписываем все простые суждения (т.е. суждения степени 0), которые входят в суждение C, пусть их число будет n.
2. Высчитываем число k строк в таблице по формуле k = 2n.
3. В столбцах входа таблицы выписываем все возможные комбинации истинностных значений простых суждений в следующем порядке: в самом правом столбце чередуем И и Л, во втором справа столбце чередуем два значения И и два значения Л, в третьем — четыре значения И подряд с четырьмя значениями Л подряд, в четвертом — восемь значений И подряд и восемь значений Л подряд, ... в l-м столбце — справа — 2 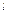 -1 значений И подряд с 2
-1 значений И подряд с 2 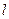 -1 значений Л подряд.
-1 значений Л подряд.
4. На выходе таблицы по порядку слева направо выписываем все суждения степени 1.
5. Для каждого суждения степени 1 при помощи таблиц для логических союзов и значений, которые принимают входэщие в него простые суждения в данной строке, выписываем истинностное значение этого суждения в виде столбца под этим суждением.
6. Выписываем все суждения степени 2 по порядку слева направо.
7. Для каждого суждения степени 2 при помощи таблиц для логических союзов и истинностных значений простых суждений и суждений степени 1 выписываем его столбец истинностных значений и т.п. вплоть до степени m, которую имеет наше исходное суждение.
8, 9 и далее. Выписываем суждения степени 3, 4 и т.д. до степени m и выписщваем столбцы их значений. Последний столбец даст нам истинностные значения суждения C.
Пример 1. Рассмотрим сложное суждение «Если бы Иван IV был бы зол по природе или не заботился об интересах государства, то он не отменил бы опричнины».
Выявим его логическую форму. Для этого суждение «Иван IV был зол по природе» обозначим через p, суждение «Иван IV заботился об интересах государства» — через q, суждение «Иван IV отменил бы опричнину» — через r.
Тогда запись нашего суждения в ЯЛС будет выглядеть так:
(p 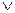
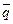 )®
)® 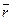
Построим истинностную таблицу для этого суждения:
1—3. Простые суждения, входящие в наше сложное суждение, — p, q, r. Поэтому вход таблицы будет выглядеть следующим образом:
| p | q | r | |
| И | И | И | |
| И | И | Л | |
| И | Л | И | |
| И | Л | Л | |
| Л | И | И | |
| Л | И | Л | |
| Л | Л | И | |
| Л | Л | Л |
Всего в таблице получилось 23 = 8 строк.
4. Выписываем суждения степени 1. Это и 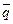 и
и 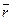 .
.
5. Выписываем их истинностные значения:
| p | q | r | 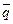
| 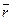
| |
| И | И | И | Л | Л | |
| И | И | Л | Л | И | |
| И | Л | И | И | Л | |
| И | Л | Л | И | И | |
| Л | И | И | Л | Л | |
| Л | И | Л | Л | И | |
| Л | Л | И | И | Л | |
| Л | Л | Л | И | И |
6. Выписываем суждения степени 2. Это — p 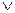
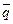 .
.
7. Выписываем его истинностное значение:
| p | q | r | 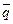
| 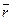
| p 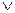 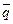
| |
| И | И | И | Л | Л | И | |
| И | И | Л | Л | И | И | |
| И | Л | И | И | Л | И | |
| И | Л | Л | И | И | И | |
| Л | И | И | Л | Л | Л | |
| Л | И | Л | Л | И | Л | |
| Л | Л | И | И | Л | И | |
| Л | Л | Л | И | И | И |
8. Выписываем суждения степени 1. Это и есть наше исходное суждение.
9. Выписываем его истинностное значение:
| p | q | r | 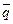
| 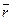
| p 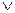 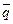
| (p 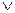 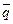 )® )® 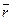
| |
| И | И | И | Л | Л | И | Л | |
| И | И | Л | Л | И | И | И | |
| И | Л | И | И | Л | И | Л | |
| И | Л | Л | И | И | И | И | |
| Л | И | И | Л | Л | Л | И | |
| Л | И | Л | Л | И | Л | И | |
| Л | Л | И | И | Л | И | Л | |
| Л | Л | Л | И | И | И | И |
Такова наша итоговая таблица. Обратите внимание, что при вычислении значения последней импликации первым следует учитывать значения третьего столбца выхода, поскольку это значения антецедента (основания) импликации, а вторым — второго столбца выхода, поскольку это значение консеквента (следствия) импликации.
Мы видим, что наше суждение истинно в пяти случаях и ложно в трех. И, что главное, мы теперь знаем, каким должен быть мир, чтобы наше суждение было истинным или, наоборот, ложным.
Пример2. Рассмотрим следующее сложное суждение:
(((p®q)  p) ®q)
p) ®q) 
Наш алгоритм построения таблицы осуществим в уме, а я выпишу только результат:
| p | q | p®q | (p®q)  p p
| (((p®q)  p) ®q) p) ®q)
| |
| И | И | И | И | И | |
| И | Л | Л | Л | И | |
| Л | И | И | Л | И | |
| Л | Л | И | Л | И |
Как мы видим, результат получился удивительным: все значения оказались И. Это означает, что это суждение истинно при всех значениях, входящих в него простых суждений.
Пример3. Рассмотрим следующее сложное суждение:
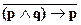
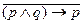
| p | q | p 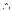 q q
| (p 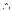 q)®p q)®p
| 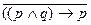
| |
| И | И | И | И | Л | |
| И | Л | Л | И | Л | |
| Л | И | Л | И | Л | |
| Л | Л | Л | И | Л |
Результат получился не менее удивительным — во всех строках наше суждение приняло значение «ложь»!
Наш опыт построения таблиц показывает, что вообще могут быть суждения трех типов:
Сложные суждения, которые во всех строках таблицы принимают значение «истина», назовем логически истинными.
Сложные суждения, которые во всех строках таблицы принимают значение «ложь», назовем логически ложными.
Сложные суждения, среди истинностных значений которщх встречаются и истина, и ложь, назовем фактическими[37].
Особенность первых двух видов суждений заключается в том, что их истинность или ложность не зависит от истинности или ложности простых суждений, которые их составляют. Они истинны или ложны просто в силу определенных соединений составляющих их суждений при помощи логических союзов. Каков бы ни был мир, т.е. какие бы простые суждения ни были в нем истинны, эти суждения всегда будут истинными или всегда ложными.
Другое дело суждения, которые мы с вами назвали фактическими. Они иногда истинны, а иногда ложны. И зависит это от состояния, в котором находится внешний мир, от того, какие простые суждения в этом мире истинны, а какие ложны. Если, например, p — Л, q — Л, r — И, то сложное суждение (p 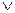
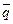 )®
)® 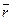 является ложным, а если все три простые суждения ложны, то это суждение истинно.
является ложным, а если все три простые суждения ложны, то это суждение истинно.
Таблицы истинности подсказывают нам некоторые простые отношения между нашими сложными суждениями и миром.
Комбинацию значений, которую простые суждения принимают в какой-либо строке на входе таблицы, назовем состоянием мира.
Если сложное суждение C принимает значение «истина» в данной строке, то будем говорить, что оно подтверждается данным состоянием мира.
Если сложное суждение C принимает значение «ложь» в данной строке, то будем говорить, что С опровергается данным состоянием мира.
Теперь мы можем ввести важные понятия подтверждаемости и опровержимости суждений.
Суждение C назовем подтверждаемым, если оно подтверддается хотя бы одним состоянием мира.
Суждение C назовем опровержимым, если оно опровергается хотя бы одним состоянием мира.
Таким образом, суждение из нашего первого примера одновременно подтверждаемо и опровержимо, суждение из второго примера — подтверждаемо, но не опровержимо, суждение из третьего примера — опровержимо, но не подтверждаемо.
Теперь мы можем высказать несколько важных соображений о науке с точки зрения тех знаний, которые мы приобрели при построении таблиц истинности. Логика интересуетсэ логически истинными и логически ложными суждениями. Это — область ее исследования. А в область исследования каких наук попадают суждения, которые не являются ни логически ложными, ни логически истинными? Ответ нам подсказывает само их название «фактические». Это означает, что они попадают в область наук, которые занимаются открытием и обобщением фактов, т.е. тех наук, которые, в отличие от логики и математики, называются эмпирическими: физики, биологии, химии, географии, истории и т.п.
Но какие же суждениэ ценятся более всего в эмпирических науках? Как ни странно, но наши таблицы могут подсказать нам ответ на этот вопрос.
Введем понятие вероятности суждения.
Вероятность суждения C, обозначим ее p(C), определяется отношением состояний мира, подтверждающих это суждение, к общему числу состояний мира в таблице для этого суждения.
Иначе говоря, p(C)= 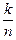 , где k — число состояний мира, подтверждающих это суждение, n — общее число состояний мира для данного суждения.
, где k — число состояний мира, подтверждающих это суждение, n — общее число состояний мира для данного суждения.
Нетрудно убедиться, что 0 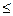 p(C)
p(C) 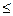 1.
1.
Наши таблицы сразу подсказывают нам, какое суждение больше сообщает нам о мире. Эту характеристику суждений обычно называют информацией.
Основатели логической теории информации Р. Карнап и И. Бар-Хиллел предложили следующее уточнение нашего интуитивного представления об информативности наших суждений:
Через И(C) обозначим количество информации, сообщаемое суждением C. Тогда:
И(C) = 1 — p(C)
Отсюда следует, что чем больше вероятность суждения, рем меньше сообщаемая им информация, и наоборот.
Суждение из примера 1 будет иметь вероятность 5/8, а информация, следовательно, 3/8.
Суждение из примера 2 будет иметь вероятность 1, а информацию 0.
Суждение из примера 3 будет иметь вероятность 0, а информацию 1.
Цель эмпирических наук может быть описана при помощи комбинации идей истины и информации. Наука, безусловно, стремится к истине. Но если ограничиваться только этой идеей, то получится, что самые лучшие суждения для науки - логически истинные. Но мы теперь знаем: хотя эти суждения очень надежные, они, тем не менее, не сообщают нам о мире никакой информации. Поэтому в цель науки следует ввести также и идею информации. Наука стремится к истинным информативным суждениям, т.е. суждениям одновременно истинным и обладающим как можно большей информацией. Но мы уже видели, что идеи истинности и информативности в определенной мере исключают друг друга, так как чем информативнее суждение, тем меньше вероятность, чтм оно истинно. Это эвристическое противоречие между идеями, составляющими цель науки, дает науке один из источников ее развития.
§ 4 Запись категорических суждений и силлогизмов при помощи языка логики предикатов
В языке логики суждений (ЯЛС), который мы рассматривали в § 3 главы 8 суждения рассматриваются как неделимые целые, их внутренняя структура не подвергается анализу. Этот язык достаточен для формализации умозаключений логики суждений, поскольку там не надо вникать во внутреннюю структуру суждений. Однако умозаключения, основанные на внутренней структуре суждений, не могут быть формализованы в этом языке.
Если мы хотим записывать в нашем языке единичные, частные и общие суждения, которые необходимы нам для обсуждения умозаключений, основывающихся на внутренней структуре высказываний, то мы должны несколько расширить наш язык и превратить его из языка логики суждений в так называемый язык логики предикатов. Язык логики предикатов был изобретен для формализации дедуктивных умозаключений. В частности, при его помощи можно выразить логические формы силлогизмов, т. е умозаключений, которые основываются на внутренней структуре суждений. Кроме того, язык логики предикатов позволяет формализовать большой класс рассуждений, которые выходят за пределы силлогистики, но широко применимы как в математических доказательствах[38], так и в обычной жизни. Мы не будем строить этот язык формально, для наших целей достаточно только показать способ записи единичных, частных и общих суждений на этом языке.
В § 3 главы 1 мы уже описывали возможность записи единичных суждений при помощи обозначений индивидуальных предметов: a, b, c, d, a1, b1 , c1 ..., и знаков для свойств и отношений этих предметов, которые мы впредь бсдем называть предикатами этих предметов: M, P, Q, R, S, и т.п. Сейчас я введу этот язык более систематически. На языке логики предикатов (ЯЛП) можно записывать наши суждения об объектах, выявляя при этом внутреннюю структуру суждений. Такое более глубокое, чем это делает ЯЛС, проникновение в суждения, позволяет создавать модели тех рассуждений, которые не могли быть построены на языке логики суждений. Для начала рассмотрим несколько суждений и их возможные способы записи на ЯЛПе.
Пример. Рассмотрим суждение "Этот лебедь белый". Если обозначить "этот лебедь" при помощи символа а, а признак "быть белым" при помощи символа Р, то единичное суждение "Этот лебедь белый" будет выглядеть так:
Р(а)
Эту запись можно прочесть так: «Признак Р принадлежит предмету а", “Предикат Р принадлежит предмету” а или "а есть Р", или, если вспомнить обозначение функций в математике, «Р от а»
Чтобы говорить о более, чем одном предмете, при помощи частных и общих суждений, нам нужно ввести в язык знаки, которые могут обозначать сразу много предметов.
В языке логики предикатов это делается при помощи предметных переменных, т.е. знаков, которые обозначают не отдельный предмет, а могут обозначать любой предмет из некоторого множества. В качестве множества, из которого заимствуются значения таких знаков может быть выбрано любое множество: стульев, людей, баянистов, лягушек, сонат, русалок, всех предметов. В логике иногда говорят, что предметная переменная "пробегает" по этому множеству. В качестве нредметных переменных мы будем использовать маленькие буквы из конца латинского алфавита: x, y, z, x1 , y2 , z1, ... , набранные курсивом.  В дальнейшем мы будем говорить, что эти предметные переменные могут обозначать любой предмет из нашего универсума рассуждения, если, конечно, не оговорено какое-нибудь специальное условие, например, что в данном суждении или рассуждении они будут обозначать только натуральные числа, людей и т.п.
В дальнейшем мы будем говорить, что эти предметные переменные могут обозначать любой предмет из нашего универсума рассуждения, если, конечно, не оговорено какое-нибудь специальное условие, например, что в данном суждении или рассуждении они будут обозначать только натуральные числа, людей и т.п.
Теперь нам осталось только ввести специальные обозначения, позволяющие записывать на нашем языке количество суждений: т.е. указывать частное это суждение или общее. В качестве таких обозначений мы будем использовать специальные знаки для слова "существует"[39], и для слова "все"[40]. Знак " 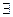 ", соответствующий слову «существует», мы будем называть квантор существования, а знак "
", соответствующий слову «существует», мы будем называть квантор существования, а знак " 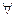 ", соответствующий слову «все», - квантор общности. При помощи знака "
", соответствующий слову «все», - квантор общности. При помощи знака " 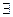 " мы будем записывать частные суждения, а при помощи знака "
" мы будем записывать частные суждения, а при помощи знака " 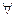 " - общие.
" - общие.
Запись " 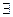 хР(х)" будет означать, что «существует предмет, назовем его х, который имеет признак Р», или «по крайней мере один х имеет признак Р», или «некоторые х имеют признак Р».
хР(х)" будет означать, что «существует предмет, назовем его х, который имеет признак Р», или «по крайней мере один х имеет признак Р», или «некоторые х имеют признак Р».
Запись " 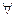 хР(х)" будет означать, что для всякого предмета х верно, что этот предмет имеет признак Р, или «каждому х присуще свойство Р» и т. п.
хР(х)" будет означать, что для всякого предмета х верно, что этот предмет имеет признак Р, или «каждому х присуще свойство Р» и т. п.
Запись " 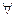 х
х 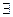 y R(х,у)" означает, что для всякого предмета х существует такой у, что между х и у имеется отношение R.
y R(х,у)" означает, что для всякого предмета х существует такой у, что между х и у имеется отношение R.
Нетрудно заметить, что наши знаки P, Q, R, S могут применяться к разному числу предметов. Это зависит от того, какие свойства или отношения обозначаются при помощи данных знаков.
Пример. Пусть х, у - предметные переменные, "пробегающие" по множеству натуральных чисел. Тогда запись 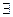 х
х 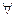 у(х
у(х 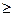 у) будет означать "существует наибольшее натуральное число". (Буквальное прочтение: «существует такое натуральное число х, что для всякого натурального числа у число х больше или равно y.)
у) будет означать "существует наибольшее натуральное число". (Буквальное прочтение: «существует такое натуральное число х, что для всякого натурального числа у число х больше или равно y.)
После этих предварительных соображений можно ввести алфавит языка логики предикатов:
a, b, c, d, a1 b1, c1, d1, a2, ... - предметные константы, служащие именами для конкретных предметов.
x, y, z, x1 , y1 , z1, x2, ... – предметные переменные, о которых речь шла раньше.
M, P, Q, R, S, M1, P1, Q1, R1, S1, P2, …- знаки предикатов (признаков).
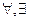 - знаки для кванторов общности и существования.
- знаки для кванторов общности и существования.
Для предметных констант и предметных переменных мы введем общее имя – терм и будем обозначать их t1, t2, t3 и т п.
Чтобы научиться строить выражения языка логики предикатов и записывать суждения при помощи ЯЛП надо построить определение суждения в языке логики предикатов подобное тому, которое мы построили для ЯЛС в § 3 главы 6.
Пусть Р обозначает произвольный предикат (т. е. знаки из п. 3 нашего алфавита). Тогда
Если P есть n-местный предикатный знак, а t1,t2,…,tn – термы, то P(t1,t2,…,tn) – суждение логики предикатов.
Если А и В есть суждения логики предикатов, то (А  В), (A
В), (A 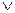 B), (A
B), (A 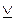 B), (A®B), (A
B), (A®B), (A 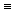 B), (
B), ( 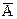 ) — суждения логики предикатов[41].
) — суждения логики предикатов[41].
Если А есть суждение логики предикатов, то 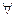 хА и
хА и 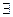 хА – суждения логики предикатов.
хА – суждения логики предикатов.
Ничто иное не является суждением логики предикатов.
Несложно заметить, что ЯЛП является расширением ЯЛСа, т. е. все суждения, которые можно записать в ЯЛСе можно записать и в ЯЛПе, но не наоборот.
Пример. В соответствии с этим определением, если P – двухместный предикатный знак, а1 – предметная константа, а х1 – предметная переменная, то P(a1, x1) – суждение логики предикатов.
Пример. P(a1)  Q(x2, x4) – суждение логики предикатов.
Q(x2, x4) – суждение логики предикатов.
Пример. 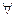 х2
х2 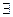 х4(P(a1)
х4(P(a1)  Q(x2, x4)) – суждение логики предикатов[42].
Q(x2, x4)) – суждение логики предикатов[42].
Пример. 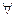 х1P(x1) ®
х1P(x1) ® 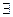 y2Q(y2) – суждение логики предикатов[43].
y2Q(y2) – суждение логики предикатов[43].
С помощью языка логики предикатов легко записывать суждения, в которых определено их количество.
Пример. «Каждый юноша любит какую-нибудь девушку» – это суждение можно перевести на язык логики предикатов следующим образом:
Обозначим предикат «быть юношей» через Р, предикат «быть девушкой» – через Q, предикат «любить» через R, выберем две предметные переменные х и у с областью изменения D = {люди}. Тогда наще суждение можно записать следующим образом:
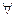 х
х 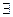 y((P(x)
y((P(x)  Q(y)→R(x, y))
Q(y)→R(x, y))
Заметим, что мы интерпретируем «какую-нибудь» в смысле «существует». Если бы мы проинтепретировали «какую-нибудь» при помощи квантора общности, то получилось бы следующее суждение:
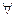 х
х 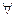 y((P(x)
y((P(x)  Q(y)→R(x, y)),
Q(y)→R(x, y)),
которое можно было бы перевести на русский язык как “Все юноши любят всех девушек” или «Каждый юноша любит каждую девушку», что было бы некоторым преувеличением.
Этот пример наводит нас на мысль, что ЯЛПе можно записать и наши категорические суждения, которые мы описывали в § 2 главы 8 и использовали в силлогизмах.
Общеутвердительное суждение А: Все S есть P.
Мы помним, что для истинности этого суждения достаточно, чтобы его термины вступали в следующее отношение:

Рис. 1
В таком случае мы можем выразить это соотношение терминов общеутвердительного суждения следующим образом: Для всякого предмета если мн есть S, то он есть P. Правильность такого истолкования видна непосредственно из рисунка. Эту фразу уже легко выразить при помощи ЯЛП:
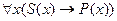
Это выражение ЯЛП мы будем считать переводом общеутвердительного суждения[44].
Общеотрицательное суждение Е: Ни один S не есть P.
Мы помним, что для истинности этого суждения достаточно, чтобы его термины вступали в следующее отношение:
Рис. 2
В таком случае мы можем выразить это соотношение терминов общеотрицательного суждения следующим образом: Для всякого предмета если он есть S, то он есть не-P. Правильность такого истолкования видна непосредственно из рисунка. Эту фразу уже легко выразить при помощи ЯЛП:
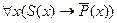
Частноутвердительное суждение I: Некоторые S есть P.
Мы помним, что для истинности этого суждения достаточно, чтобы его термины вступали в следующее отношение:

Рис. 3
В таком случае мы можем выразить это соотношение терминов частноутвердительнмго суждения следующим образом: Существует по крайней мере один такой предмет, что он есть S и он есть P. Правильность такого истолкования видна непосредственно из рисунка. Эту фразу уже легко выразить при помощи ЯЛП:
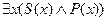
Частноотрицательное суждение О: Некоторые S не есть P.
Здесь даже не прибегая к схемам можно сказать, что это суждение переформулируется следующим образом: Существует по крайней мере один S, который есть не-P. А суждение в такой форме уже легко записать на ЯЛПе:
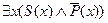 .
.
Мы получили запись на языке логики предикатов наших категорических суждений. Это довольно интересный способ записи, поскольку он вообще иллюстрирует характер перевода с одного языка на другой. В данном случае мы имеем дело с двумя логическими языками. Язык силлогистики и категорических суждений основан на следующей схеме анализа выражений:
(СП) субъект – связка – предикат.
Язык логики предикатов основан на другой схеме анализа выражений:
(ФА) функтор – аргумент,
где функтор есть знак функции. Функтор вместе с аргументом обозначает функцию. Это – не только два языка, но в каком-то смысле две концептуальные системы, т. е. системы понятий, основывающиеся на разных предпосылках о структуре мира. Поэтому и получается, что простое суждение с точки зрения силлогистики превращается в сложное суждение с точки зрения логики предикатов. При этом приходится явно вводить логические связки логики суждений (импликация, конъюнкция), которые обозначают связи между суждениями. При таком переводе изменяется логическая форма высказывания, а это влияет и на его смысл. Перевод категорических суждений на ЯЛП иллюстрирует тот общий лингвистический факт, что при переводе с одного языка на другой наши суждения изменяются. Перевод всегда творческое дело.
При помощи ЯЛСа мы не могли записать наши силлогизмы, потому что последние основываются на анализе внутренней структуры высказываний, тогда как ЯЛС не принимает ее во внимание. ЯЛП позволяет записать силлогистические умозаключения.
ГЛАВА 7
ОТНОШЕНИЯ МЕЖДУ СУЖДЕНИЯМИ
§ 1. Отношения между простыми суждениями
Ав: Давайте поспорим!
Сс: Это что? Спор ради спора?
Ав: Нет, спор ради учебных целей. Но раз вы не хотите спорить, давайте поговорим о споре. Это проще. Начнем с того, что в споре, как правило, высказываются противоположные мнения.
Ст: А, я помню. В "Двенадцати стульях" спорят Остап Бендер и Инженер. Первый говорит: "Выношу мебель". Второй говорит: "Нет, не выносите!", а Остап Бендер опять говорит: "Как же "не выношу", когда выношу!"
Ав: Очень хороший пример того, как не следует спорить. Дело в том, что здесь нет никаких аргументов в пользу той или иной точки зрения. Но это дейсрвительно начало спора, поскольку выдвинуто два противоположных суждения и каждая сторона отстаивает свое. Поэтому, чтобы спорить грамотно, следует представлять себе, какое суждение противоположно какому. Например, представим, что ваш оппонент (так называется лицо, придерживающееся в споре противоположного вашему мнения) говорит: "Все великие люди низкого роста". Как вы будете спорить с этим мнением, какое противоположное мнение вы выскажете?
Сс: Все великие люди высокого роста.
Ав: Да, это достаточно протиаоположно, но легко ли отстаивать такое мнение?
Ст: Я думаю, не очень легко, потому что мы знаем многих великих людей невысокого роста.
Ав: Высказав такое суждение, вы не очень многое выиграете в этом споре. А нельзя ли придумать какое-либо суждение, также противоположное или даже противоречащее высказанному мнению, но такое, чтобы его было легче отстаивать?
Ст: Можно. Некоторые великие люди высокого роста.
Ав: Ага, это уже лучше. Но действительно ли это суждение так уж противоположно высказанному? Ведь здесь еще можно открыть дополнительный спор, выясняя отношение между терминами "низкий" и "высокий". А этот дополнительный спор может дать возможность вашему оппоненту ускользнуть от вас.
Сс: Это вы придираетесь!
Ав: Почему придираюсь? Пожалуйста, вот вам суждение: "Некоторые великие люди не являются людьми низкого роста". Как, противоположно ли оно высказанному суждению?
Ст: Да, похоже, что да. Оно полностью отрицает то, что было сказано в начале, и не утверждает слишком многого, что трудно было бы защищать, и к тому же не содержит проблем с анализом соотношения терминов. С таким суждением наперевес легко вести спор.
Ав: А что мне позволило быстро и аккуратно сформулировать такое суждение?
Сс:Ну, конечно, Вы скажете: "логическая культура".
Ав: Это, хотя и правильный, но очень общий ответ. Я хотел сказать только об одной составляющей логической культуры - умении обращаться с отношениями между суждениями.
Ст:Да, сразу у нас это не вполне получилось, хотя, вроде бы, все было ясно.
Ав: Кстати, здесь еще возникают и другие вопросы. Например, могу ли я, отрицая мнение о том, что "Все великие люди низкого роста", в то же время признавать суждение "Некоторые великие люди - низкого роста" или мне обязательно придерживаться мнения о том, что "Все великие люди не низкого роста", и много других подобных проблем. Поэтому, вступая в спор, необходимо знать, какие суждения совместимы друг с другом, а какие - нет, к чему обязывает принятие суждений, а к чему - нет и т.п.
Сс: Это интересно.
Ав: Не только интересно, но и чрезвычайно важно. В том же споре нужно соображать, как правило, быстро. А если вы каждый раз будете заново осмысливать отношения между суждениями, то дадите своему оппоненту фору. Значит, отношения надо не только знать, но и превратить обращение с ними в навык, т.е. приобрести логическую культуру.
Сс: Ну, вот все-таки Вы сели на своего любимого конька!
Ав: Повторение - мать учения!
Разобьем наше рассмотрение отношений между суждениями на две части в соответствии с видами суждений - простыми и сложными, а среди простых суждений выделим наиболее для нас важные категорические суждения.
Терминологию позаимствуем из классификации отношений между понятиями. Для начала мы рассмотрим отношения сравнимости-несравнимости.
Рассмотрим произвольные категорические суждения С и В, в которых субъект и предикат выражены различными понятиями и которые не являются ни логически истинными, ни логически ложными (как, например, суждение "Все S есть S" или "Ни одно S не есть S").
Суждения С и В назмвем сравнимыми, если их термины совпадают с точностью до перестановки.
Суждения С и В назовем несравнимыми, если в суждении В встречается хотя бы один термин, не входящий в С.
Пример. Суждения "Все студенты являются веселыми людьми" и "Все веселые люди являются студентами" сравнимы, а суждения "Все студенты являются веселыми людьми" и "Все студенты являются находчивыми людьми" - несравнимы, так как во втором суждении встречается термин, не входящий в первое.
Сравнимые суждения С и В назовем совместимыми, если они могут быть вместе истинными.
Сравнимые суждения С и В назовем несовместимыми, если они не могут быть вместе истинными.
Пример. Суждения "Все великие люди низкого роста" и "Некоторые великие люди низкого роста" совместимы, так как в случае истинности первого суждения второе также истинно, а суждения "Все великие люди низкого роста" и "Некоторые великие люди не являются людьми низкого роста" - несовместимы, ибо они не могут быть одновременно истинны.
У каждого такого типа отношений есть свои виды. Так, отношения совместимости делятся на отношения подчинения и дополнительности. Отношения несовместимости - на отношения противоположности и противоречия.
Для систематизации и наглядного представления этих отношений еще в Средние века был придуман так называемый "логический квадрат", который выглядит следующим образом:

Рис. 1
Логический квадрат позволяет легко запомнить характеристики логических отношений между категорическими суждениями.
Охарактеризуем каждое из этих отношений в отдельности.
Дата добавления: 2015-11-04; просмотров: 1307;
