Рассмотрим задачу сравнения нескольких (более двух) дисперсий нормальных генеральных совокупностей.

Имеем l генеральных совокупностей X₁, X₂,…,X_l , которые распределены нормально. Из этих совокупностей извлечены независимые выборки, вообще говоря, различных объемов п₁, п₂,…,п_l.Случай выборок одинакового объема будет рассматриваться в данном параграфе несколько позднее. По выборкам найдены исправленные выборочные дисперсии .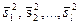

Требуется по исправленным выборочным дисперсиям при заданном уровне значимости 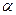проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:

.

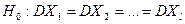Иными словами, требуется установить, значимо или незначимо различаются исправленные выборочные дисперсии. Такую гипотезу принято называть гипотезой об однородности дисперсий.

Напомним, что числом степеней свободы дисперсии 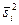называют число, на единицу меньше объема выборки, т.е. 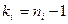. Введем случайную величину 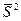– среднюю арифметическую исправленных дисперсий, взвешенную по числам степеней свободы:

, .

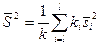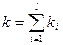На основе этой случайной величины строится критерий Бартлетта

,

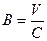где

,

.

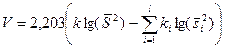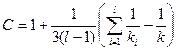Бартлетт установил, что случайная величина 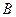при условии справедливости нулевой гипотезы распределена приближенно как 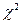с с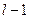тепенями свободы. Должно также выполняться условие

,

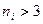т.е. объем каждой из выборок должен быть не меньше 4.

Критическую область строят правостороннюю. При этом, исходят из требования, чтобы вероятность попадания критерия в эту область( в предположении справедливости нулевой гипотезы) была равна принятому уровню значимости:

.

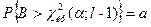Критическую точку 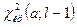находят из таблицы приложения 5, по уровню значимости 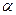и числу степеней свободы 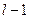. Тогда правосторонняя критическая область определяется неравенством

,

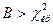а область принятия гипотезы – неравенством

.

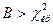Наблюдаемое значение критерия Бартлетта будем обозначать через .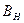

Правило проверки нулевой гипотезы будет следующим. Для того чтобы при заданном уровне значимости 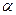проверить нулевую гипотезу об однородности дисперсий нормальных совокупностей, надо вычислить наблюдаемое значение критерия Бартлетта 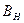. Затем, по таблице критических точек распределения 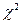найти критическую точку . Если окажется, что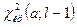

,

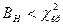то нет оснований отвергать нулевую гипотезу. В противном случае она отвергается.

В учебнике приведены конструктивные замечания по критерию Бартлетта. Приведем их.

Замечание 8. 2. Константа 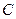, входящая в критерий Бартлетта, всегда больше единицы. Это обстоятельство следует учитывать при расчетах.

Замечание 8. 3. Критерий Бартлетта весьма чувствителен к отклонениям распределений от нормального, поэтому к выводам, полученным по этому критерию, надо относиться с осторожностью( либо достоверно проверять, что совокупности распределены приближенно нормально).

Пример 8. 5. Даны три независимые выборки из нормальных генеральных совокупностей:

,

,

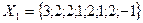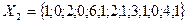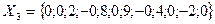
При уровне значимости 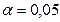проверить гипотезу об однородности дисперсий (критическая область односторонняя).

Решение. Опуская подробности расчетов, сведем предварительные результаты табл. 1

Табл.8. 1. Расчетная таблица к примеру 8. 5

№Выборки і	Объем вы- борки	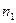Число степеней свободы	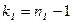Исправлен-ная дис- персия
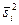
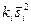
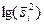
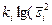
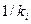
			1,428571		0,154902	1,084314	0,142857
			0,715636	7,156364	-0,14531	-1,45308	0,1
			1,2	9,6	0,079181	0,63345	0,125
∑		k=25		26,75636		0,264688	0,367857

Используя расчетную табл. 8. 1, найдем значение средней арифметической исправленных дисперсий, взвешенной по числам степеней свободы:

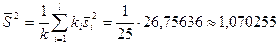
Вычислим

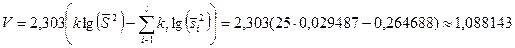
и из таблице приложения 5, по уровню значимости 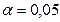и числу степеней свободы

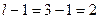
найдем критическую точку

.

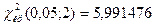Т.к.

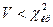
и, учитывая, что 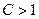, получим

.

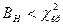Значит нет оснований отвергать нулевую гипотезу. Иными словами, исправленные выборочные дисперсии различаются незначимо.

Замечание 8. 4. Если требуется оценить генеральную дисперсию, то при условии однородности дисперсий целесообразно принять в качестве ее оценки среднюю арифметическую исправленных дисперсий, взвешенную по числам степеней свободы, т.е.

.

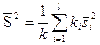Судя по примеру 8. 5, в качестве оценки генеральной дисперсии целесообразно принять 1,070255.