Сравнение двух дисперсий нормальных генеральных совокупностей. Пусть генеральные совокупности X и Y распределены нормально

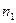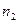Пусть генеральные совокупности X и Y распределены нормально. Из совокупностей извлечены выборки объема и , соответственно. По ним найдены исправленные выборочные дисперси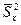и и 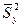. Требуется по исправленным дисперсиям при заданном уровне значимости 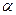проверить нулевую гипотезу. Она состоит в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:

.

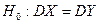В силу того, что исправленные дисперсии являются несмещенными оценками генеральных дисперсий, т.е.

,

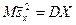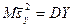
нулевую гипотезу можно записать следующим образом:

.

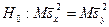Т.о. требуется проверить, что математические ожидания исправленных выборочных дисперсий равны между собой. Обычно исправленные дисперсии оказываются различными. Значимо (существенно) или незначимо различаются исправленные дисперсии?

Если окажется, что нулевая гипотеза справедлива, т. е. генеральные дисперсии одинаковы, то различие исправленных дисперсий незначимо и объясняется случайными причинами, в частности случайным отбором объектов выборки. Например, если различие исправленных выборочных дисперсий результатов измерений, выполненных двумя приборами, оказалось незначимым, то приборы имеют одинаковую точность. Если же нулевая гипотеза отвергнута, т.е. генеральные дисперсии неодинаковы, то различие исправленных дисперсий значимо и не может быть объяснено случайными причинами.

В качестве критерия проверки нулевой гипотезы о равенстве генеральных дисперсий принимают отношение большей исправительной дисперсии к меньшей, т.е. случайную величину

.

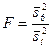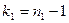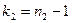Величина F при условии справедливости нулевой гипотезы имеет распределение Фишера-Снедекора со степенями свободы и , где 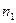– объем выборки, по которой вычислена большая исправленная дисперсия, 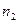– объем выборки, по которой найдена меньшая дисперсия. Распределение Фишера-Снедекора зависит только от чисел степеней свободы и не зависит от других параметров. Этот критерий называют критерием Фишера-Снедекора. Для него имеются специальные таблицы (см. приложение 7).Критическая область строится в зависимости от вида конкурирующей гипотезы.

В качестве первого случая рассмотрим нулевую гипотезу 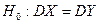и конкурирующую гипотезу 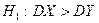. Построим правостороннюю критическую область. Потребуем, чтобы вероятность попадания критерия 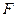в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости 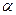, т.е.

.

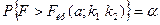Критическая точка 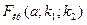находится по таблице критических точек распределения Фишера-Снедекора. Обозначим отношение большей из наблюдаемых исправленных дисперсий к меньшей, как 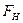. Сформулируем правило проверки нулевой гипотезы.

Для того чтобы при заданном уровне значимости проверить нулевую гипотезу 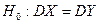о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе 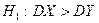, надо вычислить отношение большой исправленной дисперсии к меньшей, т.е.

.

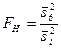По таблице критических точек распределения Фишера-Снедекора находят 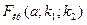. Если 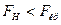, то нет оснований отвергать нулевую гипотезу. В противном же случае ее отвергают. Если использовать статистические функции из Microsoft Excel, то для нахождения 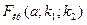надо вычислять FРАСПОБР .

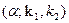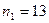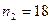Пример 8. 1. По двум независимым выборкам с объемами и , которые извлечены из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперси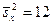и и 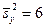. При уровне значимости 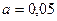проверить нулевую гипотезу 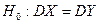о равенстве генеральных дисперсий при конкурирующей гипотезе .

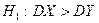Решение. Найдем отношение большей исправленной дисперсии к меньшей:

.

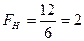Далее используем таблицу критических точек распределения F Фишера-Снедекора. По заданному уровню значимости 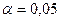и числам степеней свободы 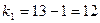и 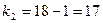находим критическую точку 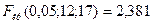. Т.к. 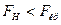, то нет оснований отвергать нулевую гипотезу о равенстве генеральных дисперсий. Использование Microsoft Excel приводит к аналогичным результатам:

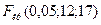=FPАСПОБР ;

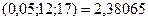В качестве второго случая рассмотрим нулевую гипотезу 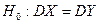и конкурирующую гипотезу 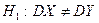. В этом случае надо строить двустороннюю критическую область. Можно доказать, что наибольшая мощность (вероятность попадания критерия в критическую область при справедливости конкурирующей гипотезы) достигается тогда, когда вероятность попадания критерия в каждый из двух интервалов критической области равна 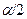. Обозначим через 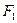левую границу критической области и через F₂ – правую. Тогда должны выполняться соотношения

, .

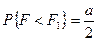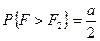Правую критическую точку 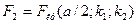находят по таблице критических точек распределения Фишера-Снедекора.

Оказывается, что левую критическую точку можно и не отыскивать. Достаточно найти правую критическую точку 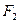при уровне значимости, вдвое меньше заданного. Тогда не только вероятность попадания критерия в «правую часть» критической области (т.е. правее 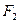) равна 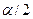, но и вероятность попадания этого критерия в «левую часть» критической области (т.е. левее F₁) также равна 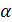/2. Т.к. эти события несовместны, то вероятность попадания рассматриваемого критерия во всю двустороннюю критическую область будет равна .

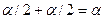Сформулируем правило проверки нулевой гипотезы о равенстве генеральных дисперсий нормально распределенных совокупностей при конкурирующей гипотеза 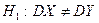. Для этого нужно вычислить отношение большой исправленной дисперсии к меньшей, т.е. 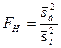. По таблице критических точек распределения Фишера-Снедекора по уровню значимости 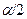(вдвое меньшем заданного) и числам степеней свободы 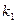и 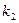( 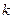– число степеней свободы большей дисперсии) найти критическую точку 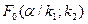. Если 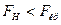, то нет оснований отвергать нулевую гипотезу. В противном же случае ее отвергают.

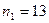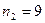Пример 8. 2. По двум независимым выборкам с объемами и , которые извлечены из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперси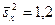и и 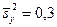. Требуется при уровне значимости 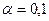проверить нулевую гипотезу 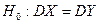о равенстве генеральных дисперсий при конкурирующей гипотезе .

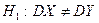Решение найдем отношением большей исправленной дисперсии к меньшей:

.

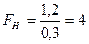Теперь используем таблиц критических точек распределения F Фишера-Снедекора. По заданному уровню значимости 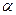/2=0,1/2=0,05 и числами степеней свободы 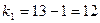и 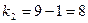находим критическую точку 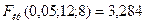. Использование Microsoft Excel приводит к аналогичным результатам:

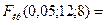FPАСПОБР .

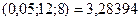Т.к. 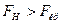, то нулевую гипотезу о равенстве генеральных дисперсий отвергаем. Другими словами, выборочные исправленные дисперсии различаются значимо. Например, если бы рассматриваемые дисперсии характеризовали точность двух методов измерений, то следует предпочесть тот метод, который имеет меньшую дисперсию (судя по нашему примеру 0,3).