Задача сравнения исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности.
Пусть генеральная совокупность распределена нормально, причем генеральная дисперсия хотя и неизвестна, но имеются основания предполагать, что она равна гипотетическому (предполагаемому) значению. На практике 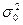 устанавливается на основании предшествующего опыта или теоретически. Пусть из генеральной совокупности извлечена выборка объема п и по ней найдена исправленная выборочная дисперсия с
устанавливается на основании предшествующего опыта или теоретически. Пусть из генеральной совокупности извлечена выборка объема п и по ней найдена исправленная выборочная дисперсия с 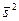
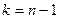 степенями свободы. Требуется по исправленной дисперсии при заданном уровне значимости проверить нулевую гипотезу, состоящую в том, что генеральная дисперсия рассматриваемой совокупности равна гипотетическому значению
степенями свободы. Требуется по исправленной дисперсии при заданном уровне значимости проверить нулевую гипотезу, состоящую в том, что генеральная дисперсия рассматриваемой совокупности равна гипотетическому значению 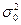 . Т.к.
. Т.к. 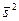 является несмещенной оценкой генеральной дисперсии, имеем нулевую гипотезу
является несмещенной оценкой генеральной дисперсии, имеем нулевую гипотезу
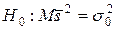 .
.
Итак, требуется проверить, что математическое ожидание исправленной дисперсии равно гипотетическому значению генеральной дисперсии. Другими словами, надо установить, значимо или незначимо различаются исправленная выборочная и гипотетическая генеральная дисперсии.
На практике рассматриваемая гипотеза проверяется, если нужно проверить точность приборов, инструментов, станков, методов исследования и устойчивость технологических процессов. Например, известна допустимая характеристика рассеяния контролируемого размера деталей, изготавливаемых станков-автоматов, равная 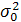 . Если найденная по выборке характеристика окажется значимо больше
. Если найденная по выборке характеристика окажется значимо больше 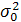 , то станок нуждается в наладке.
, то станок нуждается в наладке.
Критерием проверки нулевой гипотезы является случайная величина
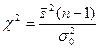 .
.
Критическая область строится в зависимости от вида конкурирующей гипотезы.
Рассмотрим первый случай. Пусть нулевая гипотеза 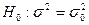 . Конкурирующая гипотеза
. Конкурирующая гипотеза 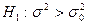 . В этом случае строят правостороннюю критическую область и требуют, чтобы выполнялось соотношение
. В этом случае строят правостороннюю критическую область и требуют, чтобы выполнялось соотношение
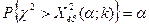 .
.
Сформулируем правило проверки нулевой гипотезы. Надо вычислить наблюдаемое значение критерия 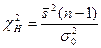 . Затем по таблице критических точек распределения
. Затем по таблице критических точек распределения 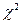 (см. приложение 5), по заданному уровню значимости
(см. приложение 5), по заданному уровню значимости 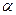 и числу степеней свободы
и числу степеней свободы 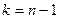 , найти критическую точку
, найти критическую точку 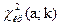 . В Microsoft Excel критическая точка находится следующим образом
. В Microsoft Excel критическая точка находится следующим образом 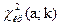 =ХИ2ОБР.
=ХИ2ОБР.
Если 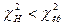 , то нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают.
, то нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают.
Пример 8. 3. Из нормальной генеральной совокупности извлечена выборка объема 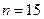 и по ней найдена исправленная выборочная дисперсия
и по ней найдена исправленная выборочная дисперсия 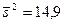 . Требуется при уровне значимости
. Требуется при уровне значимости 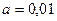 проверить нулевую гипотезу
проверить нулевую гипотезу 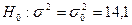 , приняв в качестве конкурирующей гипотезы
, приняв в качестве конкурирующей гипотезы 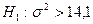 .
.
Решение. Найдем наблюдавшееся значение критерия:
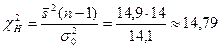 .
.
Согласно конкурирующей гипотезе, критическая область является правосторонней. Из таблицы приложения 5 по уровню значимости 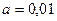 и числу степеней свободы
и числу степеней свободы 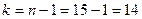 находим критическую точку
находим критическую точку 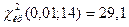 . В Microsoft Excel получаем
. В Microsoft Excel получаем 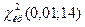 =ХИ2ОБР(14;0,01)=29,141. Т.к.
=ХИ2ОБР(14;0,01)=29,141. Т.к. 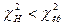 , то нет оснований отвергать нулевую гипотезу. Другими словами, различие между исправленной дисперсией 14,9 и гипотетической генеральной дисперсией 14,1 – незначимое.
, то нет оснований отвергать нулевую гипотезу. Другими словами, различие между исправленной дисперсией 14,9 и гипотетической генеральной дисперсией 14,1 – незначимое.
Рассмотрим теперь второй основной случай проверки гипотез. Нулевая гипотеза 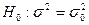 . Конкурирующая гипотеза
. Конкурирующая гипотеза 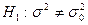 . В этом случае строят двустороннюю критическую область. При этом исходят из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости
. В этом случае строят двустороннюю критическую область. При этом исходят из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости 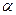 . Критические точки – левую и правую границы критической области – находят, требуя, чтобы вероятность попадания критерия в каждый из двух интервалов критической области была равна
. Критические точки – левую и правую границы критической области – находят, требуя, чтобы вероятность попадания критерия в каждый из двух интервалов критической области была равна 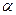 /2:
/2:
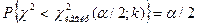 ,
, 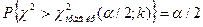 .
.
В таблице критических точек распределения указаны лишь «правые» критические точки, поэтому возникает кажущееся затруднение в отыскании «левой» критической точки. Это затруднение легко преодолеть, если принять во внимание, что события 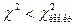 и
и 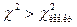 противоположны и, следовательно,
противоположны и, следовательно,
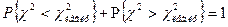
Отсюда
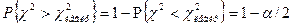 .
.
Т.е. левую критическую точку можно искать как правую (и значит, ее можно найти по таблице, исходя из требования, чтобы вероятность попадания критерия в интервал, расположенный правее этой точки, была равна 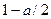 .
.
Сформулируем правило проверки нулевой гипотезы. Для того чтобы при заданном уровне значимости 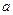 проверить нулевую гипотезу о равенстве неизвестной генеральной дисперсии
проверить нулевую гипотезу о равенстве неизвестной генеральной дисперсии 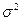 нормальной совокупности гипотетическому значению
нормальной совокупности гипотетическому значению 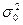 при конкурирующей гипотезе
при конкурирующей гипотезе 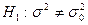 , надо вычислить наблюдаемое значение критерия
, надо вычислить наблюдаемое значение критерия 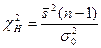 и по таблице найти левую критическую точку
и по таблице найти левую критическую точку 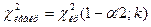 и правую критическую точку
и правую критическую точку 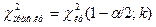 . Если окажется, что
. Если окажется, что
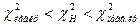 ,
,
то нет оснований отвергнуть нулевую гипотезу. Если же окажется, что 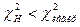 или
или 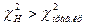 , то нулевую гипотезу отвергают.
, то нулевую гипотезу отвергают.
Пример 8. 4. Из нормальной генеральной совокупности извлечена выборка объема п=16 по ней найдена исправленная выборочная дисперсия 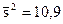 . Требуется при уровне значимости
. Требуется при уровне значимости 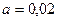 проверить нулевую гипотезу
проверить нулевую гипотезу 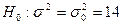 , приняв в качестве конкурирующей
, приняв в качестве конкурирующей 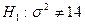 .
.
Решение. Найдем наблюдавшееся значение критерия:
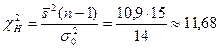
Судя по конкурирующей гипотезе, критическая область будет двусторонней. По таблицам приложения 5 находим критические точки:
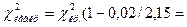
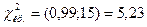 ;
;
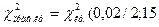 =
= 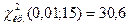 .
.
Т.к. наблюдавшееся значение критерия принадлежит области принятия гипотез:
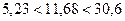 ,
,
то нет оснований ее отвергать. Другими словами, исправленная выборочная дисперсия 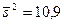 незначимо отличается от гипотетической генеральной дисперсии
незначимо отличается от гипотетической генеральной дисперсии 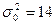 .
.
В третьем случае конкурирующая гипотеза имеет вид
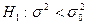 .
.
При такой конкурирующей гипотезе находят критическую точку 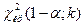 . Если окажется, что
. Если окажется, что
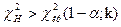 ,
,
то нет оснований отвергать нулевую гипотезу. В противоположном случае ее отвергают.
Замечание 1. Если число степеней свободны 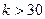 , то критическую точку можно приближенно найти по равенству Уилсона-Гилферти
, то критическую точку можно приближенно найти по равенству Уилсона-Гилферти
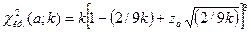 ,
,
где zα определяют из равенства
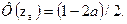
используя таблицы интегральной функции Лапласа (приложение 2).
Дата добавления: 2015-11-04; просмотров: 2913;
