Вариация технического состояния

Под влиянием условий эксплуатации, квалификации персонала, неоднородности самих изделий и их начального состояния интенсивность и характер изменения параметра технического состояния у разных изделий (автомобилей) будет различной (рис. 3). Наработка на отказ будет случайной величиной и иметь вариацию (рис. 3а), неминуема также вариация технического состояния y_i на определённом пробеге l_o и как следствие — вариация трудоемкости и продолжительности выполнения работ по восстановлению технического состояния.

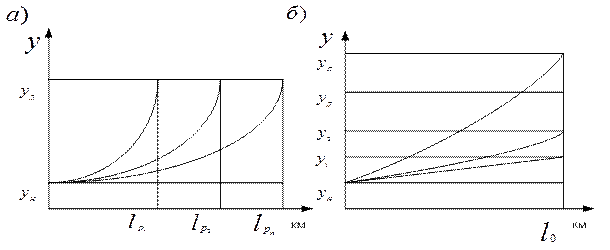
Рис.3. Вариация ресурса (а) и технического состояния (б)

Следовательно, т. к. наработка на отказ, трудоёмкость и продолжительность являются случайными величинами, важно знать характеристики случайной величины:

— среднее значение

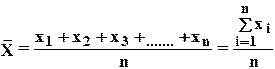(4)

— среднеквадратическое отклонение

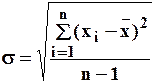(5)

— коэффициент вариации

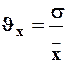(6)

Различают случайные величины:

а) Малой вариацией .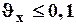

б) Средней вариацией .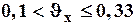

в) Большой вариацией .

Вероятность — численная мера степени объективно существующей возможности появления изучаемого события.

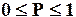(7)

Если Р = 1 — событие достоверно; Р » 0 — событие маловероятно.

Вероятность безотказной работы R(x) — отношение числа безотказной работы изделия за наработку Х к общему числу случаев.

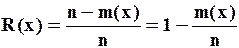(8)

где m(x) — число отказавших изделий к моменту наработки Х.

Вероятность отказа F(x) — событие противоположное вероятности безотказной работы:

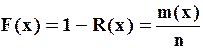(9)

Плотность вероятности отказа f(x) — вероятность отказа за малую единицу времени при работе узла, агрегата, деталей без замены.

Если 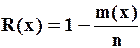, то при n = const дифференцируя, получим:

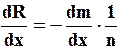(10)

где 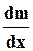— элементарная вероятность, с которой в любой момент времени происходят отказы при работе детали, агрегата без замены.

Если эту величину отнести к общему числу деталей, то получим плотность вероятности отказа.

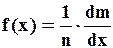(11)

учитывая, что 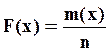, получим:

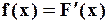(12)

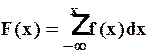
F(x) — называется интегральной функцией распределения.

f(x)— называется дифференциальной функцией распределения.

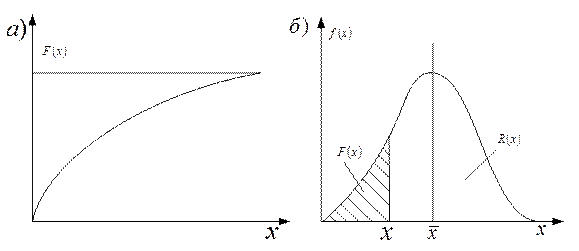
Рис. 4 Интегральная и дифференциальная функции распределения

Так как 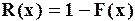, то .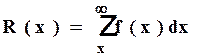

Имея значения F(x) или f(x), можно произвести оценку надежности данного изделия, т. е. определить вероятности отказа и безотказной работы и среднюю наработку до отказа:

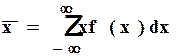(13)

Дифференциальная функция распределения f(x) иногда называется законом распределения случайной величины.

Различают несколько законов распределения случайной величины, например, нормальный закон, логарифмически — нормальный закон, закон Вейбулла-Гнеденко и т. д.

Нормальный закон — когда на протекание исследуемого процесса и его результат влияет сравнительно большое число независимых (или слабозависимых) факторов, каждый из которых, в отдельности, оказывает лишь незначительное действие по сравнению с суммарным влиянием всех остальных. Плотность вероятности распределения параметра при нормальном законе определяется по формуле

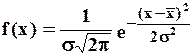(14)

тогда вероятность безотказной работы R(x) и вероятность отказа F(x) определяются:

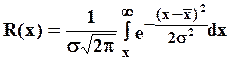(15)

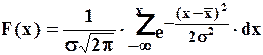
При расчетах часто пользуются понятием нормированной функции Ф(z), для которой принимается новая случайная величина — нормированное отклонение ещё её называют квантиль.

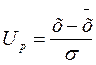, (16)

Закон Вейбулла-Гнеденко проявляется в модели так называемого "слабого звена". Если система состоит из группы независимых элементов, отказ или неисправность которых приводит к отказу всей системы, то вероятность ее безотказной работы определяется предельным отклонением.

Например, ресурс подшипника качения ограничивается одним из элементов (шарик или ролик, конкретный участок сепаратора) и описывается указанным распределением. Ряд изделий, при анализе отказа, может быть рассмотрен как состоящий из нескольких элементов (участков): прокладок, уплотнений, шлангов, трубопроводов, приводных ремней. Разрушение таких изделий происходит в разных местах при разной наработке, однако ресурс изделия в целом определяется наиболее слабым его участком.

Плотность вероятности распределения параметра при законе Вейбулла-Гнеденко определяется по формуле

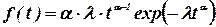, (17)

где a- параметр формы кривой распределения;

l- параметр масштаба.

Экспоненциальное распределение является частным случаем распределения Вейбулла при a=1.

Функция распределения описывается соотношением:

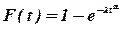(18)

Функция надежности- величина, обратная функции распределения:

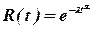(19)

Логарифмически нормальное распределение является двухпараметрическим распределением случайной величины, логарифм которой распределен по нормальному закону. Как распределение положительных величин, оно несколько точнее, чем нормальное. В теории надежности такое распределение используют для описания наработки до отказа деталей в период наступления усталости материала, а также процессов восстановления, отказов по износу, наработки на отказ подшипников качения или наработки между отказами сложных технических систем.

Плотность распределения описывается зависимостью:

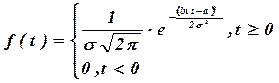(20)

Параметры a и s оценивают по результатам испытаний с помощью формул:

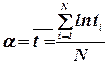(21)

где t_i -наработка до отказа i-ого изделия;

N- число изделий, поставленных на испытания.

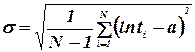(22)

Функция распределения имеет вид:

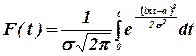(23)

или

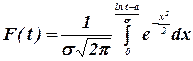(24)

Вероятность безотказной работы или отказа можно определить по таблице для нормального распределения в зависимости от значения квантиля:

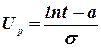(25)

Экспоненциальное распределение.

В природе, и особенно, в технике широкое применение нашел закон экспоненциального распределения. Этот закон описывает надежность работы изделия в период его нормальной эксплуатации, когда постепенные отказы ещё не проявляются и надежность характеризуется внезапными отказами. Эти отказы вызываются неблагоприятным сочетанием различных факторов и поэтому имеют постоянную интенсивность λ. Экспоненциальное распределение иногда называют основным законом надежности. Существенное достоинство этого закона состоит в том, что он имеет один параметр. Экспоненциальный закон распределения часто описывает время безотказной работы разнообразных изделий. Кроме того, этот закон используют при решении проблем, связанных с обслуживанием сложных систем, в частности, при описании закона восстановления. Экспоненциальное распределение используют также для описания времени безотказной работы системы с большим числом последовательно соединенных элементов, если каждый из элементов в отдельности не оказывает влияние на отказы системы.

Вероятность безотказной работы:

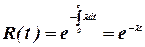, (26)

где λ- интенсивность отказов (параметр распределения)

Плотность распределения описывают соотношением:

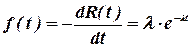(27)

Графическое изображение плотности экспоненциального распределения при λ=1

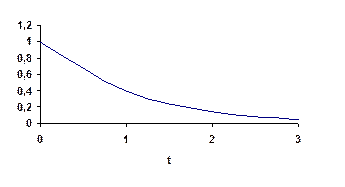
Функция распределения (вероятности отказа) выражается зависимостью:

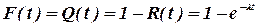, (28)

Среднеквадратическое отклонение для экспоненциального распределения равно:

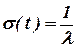, (29)

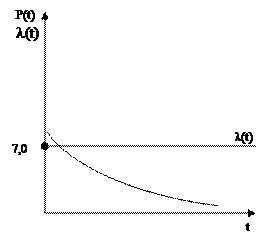Распределение Рема:

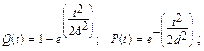
d-параметр распределения Рема.

Пример: d = 100r, t = 50r.

P(50) =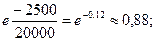

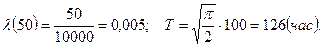
Простейший поток

Появление отказов и сбоев можно представить в виде некоторого потока случайного со временем наибольшей переменной в точности получается простейший поток, который характеризуется формулой:

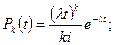
Эта формула позволяет рассчитать вероятность появление отказа в промежутке времени t. Простейший поток характеризует три свойства времени: стационарностью, отсутствием последействия, ординарностью.

Стационарность - указывает, что вероятность появления определенного числа событий за заданный период, времени который не зависит от положений этого периода на оси времени, а зависит только от его действительности.

Отсутствие последействия – характерно тем, что вероятность появления определенного числа событий за заданный период времени независящий от числа и характеризующий события, происходящие до этого времени.

Ординарность - означает не возможность одновременного появления двух и более событий.

Простейший поток получается если:

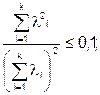l(t) = l =cons t; P(t) =e^-^l^t;

С экспоненциальным законом хорошо согласуются законы распределения отказов для сложных систем, состоящих из многих элементов.

Это объясняется тем, что закон распределения интервалов м/д соседними событиями в потоке редких случайных событий составленных из многих неизвестных потоков с любыми характеристиками, которые сходятся к экспоненциальному закону.

Закон случайных величин применим к задачам надежных изделий и их технической жизни.

(0, t₁) - первый период повышенных интенсивных отказов. Это связано с выявлением дефектов при изготовлении.

(t₁, t₂) – второй период, характеризующий постоянные значения интенсивных отказов. Это участок нормальной эксплуатации изделия.

(t₂, ¥) Третий период, характеризующий повышенную интенсивность отказов. Здесь начинается процесс старения.

Второй период характеризует эксплуатацию и распределение.

Первый и третий период характеризует распределение Вейбула.

При m < 1 распределение Вейбула можно использовать для оценки надежности изделий при наработке стажа по прошествии времени.

Методы расчета надежности.

Для расчета надежности радиоэлектронной аппаратуры в зависимости от ее надежности (не восстанавливаемость и восстанавливаемость), все зависит от режима обслуживания, от условий хранения, от структуры использования различных методов расчета надежности.

Различные методы для расчета надежности системы с учетом восстановления и без учета восстановления.

Для расчета надежности без учета восстановления используется два метода: графовероятностный и логико-вероятностный. Прежде всего, необходимо определить критерии отказа сбоя систем.

Критерии отказа систем являются нарушением способности этой системы выполнять свое назначение, при этом могут не соответствовать выходные параметры и будут применены какие от действия по известным нормам.

При создании математической модели структуры технической системы выявятся ее критерии, при которых определяется состояние элементов составляющих данную систему. В этом случае каждый из элементов может находиться в двух состояниях работоспособном и неработоспособном. Второе состояние выражает отказ системы. Состояние системы определяется совокупностью состояния ее элементов. Критерии отказа позволяют все множество элементов разделить на два подмножества

1) Характеризует состояние работоспособности системы.

2) Состояние отказа.

Для сложной структуры анализ надежности системы сводится к представлению системы в виде некоторого элемента.

Графовероятностный метод. Основывается на представлении схемы расчета надежности в виде связного двухполюсного графа, имеющего два полюса: входной и выходной. Физически это можно представить как определение возможности прохождение некоторого сигнала от входа некоторой системы характерной сетевой структуры, к выходу.

Схемы распределения надежности различают по критерию работоспособности или отказа. Всевозможные структуры систем можно свести к последовательным и комбинированным.

Последовательные системы называются системы, которые работоспособны тогда, когда работоспособны все ее элементы. Если говорить о состоянии отказа, то последовательные системы отказывают, если отказывает хотя бы один ее элемент.

Обозначим: n – число элементов в последовательной системе, а событие состояний в работоспособной 8 – го элемента через х₈, а событие состояний b работоспособность всей системы через s, тогда схема расчета надежности по критерию работоспособности и отказа будут иметь следующий вид: в дереве работоспособности базисное событие, определяемое работоспособность элементов х₈, связано между собой логическими звеньями схема расчета по критерию работоспособности изображена ниже:

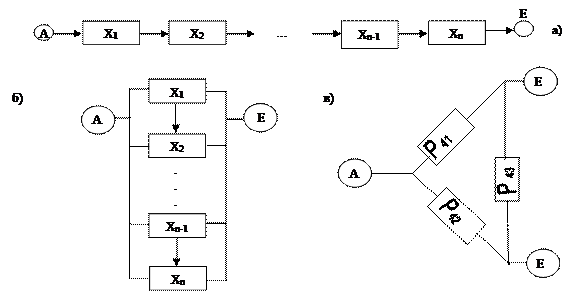
На рисунке а) соединены исходный узел А с узлом Е расчеты, на схеме расчет надежности существует тогда, когда работоспособны все ее элементы. Из рисунка а) видно, что система отказывает, если хотя бы 1 элемент. Все события на рисунках представляют схему со включенными элементами.

Надежность последовательной системы а) определяется формулой:

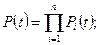
Где P_i(t) коэффициент надежности. i – его элементная система.

Параллельные системы б).

Называется такая система, которая работоспособна, если работоспособен хотя бы 1 из ее элементов, т.е. система отказывает тогда, когда отказывают все элементы. События состоят в том, что восьмой элемент работоспособен обозначим его как х₈ где х₈ = 1, 2…, n, n – число в системе. События состояния отказа s, тогда схема работоспособна и расчет по критерию работоспособности и отказа будет иметь следующий вид:

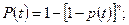
где P_i(t) –надежность i- того элемента.

Надежность схемы «два из трех» в) определяется по формуле:

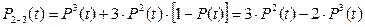Надежность системы при частичном резервировании (работоспособность системы определяется при R-исправных элементах из n элементов) определяется по формуле:

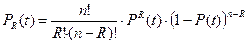Метод свертки.

Для последовательно параллельной структуры эффективным является метод свертки. Он основан на поэтапном преобразовании этой структуры в последовательные структуры.

; ;

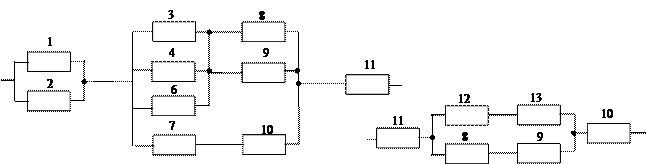
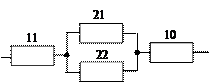
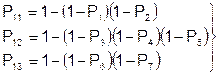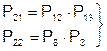P₃₁ = 1 –(1 – P₂₁)(1 – P₂₂) ==>

P = (P₁₁ · P₃₁ · P₁₀)

Не все схемы надежности можно представить в виде комбинации последовательной и параллельной. Поэтому для расчета схем используют приближенные методы.

<3 456 7 8 9 >

Дата добавления: 2015-10-26; просмотров: 1807;