Истечение жидкости через отверстие в тонкой стенке

Истечение при постоянном напореиз замкнутого сосуда показано на

рис. 5.7, а). Стенка считается тонкой, если ее толщина не превышает 0,2d (d −

диаметр отверстия). Глубину расположения отверстия h и абсолютное давление

газа над жидкостью р₀ считаем постоянными. Поэтому процесс истечения −

установившийся, и к нему можно применить уравнение Бернулли. Истечение происходит в атмосферу (наружное давление равно р_а ).

При истечении через отверстие линии тока искривляются, из-за чего происходит сжатие струи (площадь ее сечения 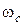меньше площади отверстия 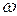). Отношение 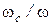называется степенью сжатия струи и обозначается .

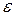При совершенном сжатии струи (когда площадь отверстия мала по сравнению с сечением сосуда, а само отверстие расположено далеко от дна) для отверстия в тонкой стенке .

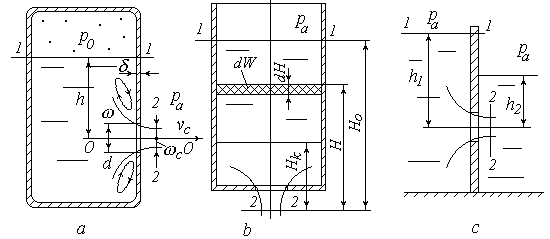
Рис. 5.7. Истечение через отверстие в тонкой стенке

Запишем уравнение Бернулли для сечений 1−1 и 2−2 (рис. 5.7, а):

.

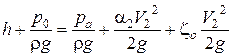Здесь 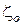− коэффициент местного сопротивления отверстия (путевые потери отсутствуют).

Перепишем это уравнение в следующем виде:

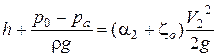. (5.15)

Обозначим 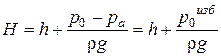. (5.16)

Величина Н называется начальным напором. Из (5.15) получим:

.

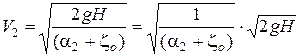Обозначим

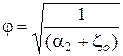(коэффициент скорости). (5.17)

При истечении через отверстие в тонкой стенке

В итоге получим формулу для скорости истечения:

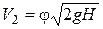. (5.18)

Расход при истечении через отверстие равен:

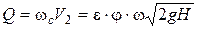. (5.19)

Обозначим 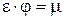(коэффициент расхода). Тогда из (5.19) получим:

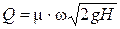. (5.20)

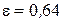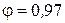При и коэффициент расхода .

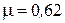Следует отметить, что приведенные численные значения коэффициентов относятся к турбулентному режиму. При ламинарном режиме истечения эти

коэффициенты зависят от числа Рейнольдса.

Истечение при переменном напорепоказано на рис. 5.7, b. Здесь

обозначены через Н₀ , Н_к , Н соответственно начальное, конечное и текущее значение напора Н, который уменьшается по мере вытекания жидкости из сосуда. Площадь сечения сосуда обозначим S, площадь отверстия – ω. Движение при этом неустановившееся, и уравнение Бернулли, строго

говоря, применять в этом случае нельзя. Однако в течение бесконечно малого отрезка времени dt напор изменяется пренебрежимо мало; поэтому на данном отрезке движение можно считать квазиустановившимся (как бы установившимся) и применять уравнение Бернулли.

Пусть за время dt уровень опустился на dH; при этом вытек объем

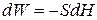(знак минус стоит, так как приращение dH отрицательно).

С другой стороны, 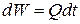. Приравняем эти выражения.

.

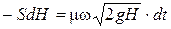Отсюда

.

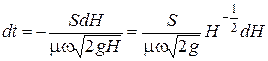Найдем время вытекания жидкости при изменении напора от Н₀ до Н_к : .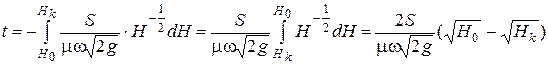

При полном вытекании ( 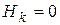) 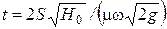. (5.21)

Подсчитаем время полного вытекания при постоянном напоре Н₀ :

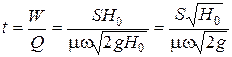(5.22)

Сравнив (5.21) и (5.22), видим, что в последнем случае время вытекания в два

раза меньше.

Истечение под уровеньпроисходит, например, при водосбросе из одного водоема в другой (рис. 5.7, с).

В отличие от предыдущих случаев истечение происходит не в атмосферу, где

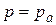, а в жидкость, где давление равно .

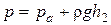Из уравнения Бернулли получим:

.

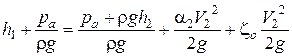После сокращения и приведения подобных членов получим:

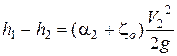или ,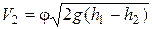

где φ − коэффициент скорости, определяемый формулой (5.16).

Для расхода получим формулу:

.

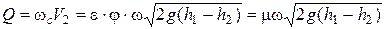Опыты показывают, что при истечении под уровень (такое отверстие называют затопленным) коэффициенты 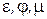можно брать такими же, как при истечении в атмосферу.