Расчет простого трубопровода постоянного сечения

Пусть имеется трубопровод с внутренним диаметром d, длиной L; его

точка входа − А с высотой z_А, точка выхода − В с высотой z_В. Известны эквивалентная шероховатость 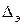и коэффициенты всех местных сопротивлений трубопровода ζ_i . По трубопроводу протекает расход жидкости Q; плотность ρ и вязкость 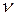которой заданы (рис. 5.2, a).

Запишем уравнение Бернулли (4.16)для сечений в точках А и В:

.

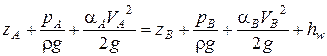Так как площади трубы в сечениях А и В одинаковы, то 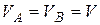, 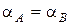; следовательно, скоростные напоры можно сократить. Кроме того, распишем выражение для общих потерь h_W . Получим:

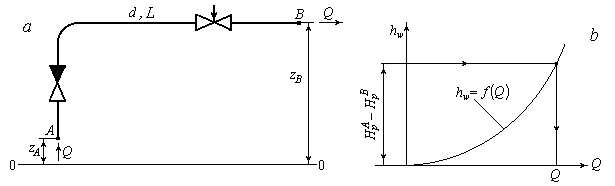
Рис.5.2. К расчету простого трубопровода постоянного сечения

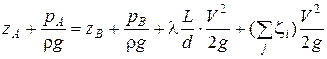. (5.4)

В этой формуле 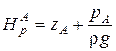; 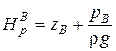− потенциальные напоры,

j − количество местных сопротивлений.

Выразим скорость V через расход по формуле 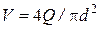. Из (5.4) получим:

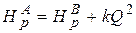, (5.5)

где k − коэффициент потерь, вычисляемый по формуле:

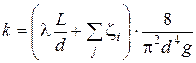. (5.6)

Формула (5.5) − компактная запись уравнения Бернулли. Ее и будем

использовать в дальнейших расчетах.

При расчете простого трубопровода постоянного сечения существует три типа задач. Рассмотрим каждую из них.

Тип 1.Заданы: d, L, 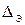, ζ_i, Q, ρ, 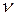, 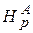. Найти .

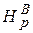При таком варианте исходных данных решение задачи наиболее простое:

1.Вычисляем среднюю скорость в трубе .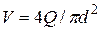

2.Вычисляем число 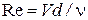и определяем режим течения.

3.Выбираем формулу для 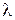и вычисляем .

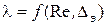4.Вычисляем коэффициент k по формуле (5.6).

5. Из формулы (5.5) определяем .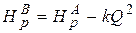

Аналогично решается задача при известном 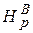и неизвестном .

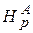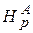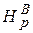Тип 2.Заданы: d, L, , ζ_i , , , ρ, 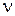. Найти Q.

При неизвестном расходе нет возможности вычислить V и Re; поэтому нельзя определить ни 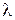, ни k. Задача может быть решена двумя методами -

численным либо графоаналитическим.

Численный метод - это метод последовательных приближений.

Последовательность операций при этом следующая:

1. Задаемся величиной допускаемой относительной ошибки вычисления расхода Е, например, 0,001 (0,1%).

2.Задаемся любым значением расхода .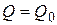

3.Вычисляем среднюю скорость в трубе .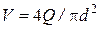

4.Вычисляем число 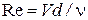и определяем режим течения.

5.Выбираем формулу для 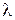и вычисляем .

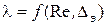6.Вычисляем коэффициент k по формуле (5.6).

7. Из формулы (5.5) определяем .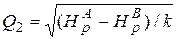

8. Если абсолютная величина 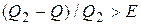, то 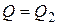; идти к 3.

Иначе 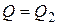(решение задачи).

Графоаналитический метод - это метод характеристик. Характеристикой трубопровода называется график зависимости . Вид ее показан на рис. 5.2, b .

Последовательность операций при этом следующая:

1. Составляем таблицу, где задаемся рядом значений расхода Q в порядке возрастания.

2. Для каждого значения расхода вычисляем 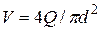, , 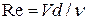определяем режим , выбираем формулу для и вычисляем 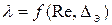, k по формуле (5.6), гидравлические потери по формуле .

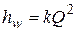3. По полученным значениям h_w строим график (рис. 5.2,b).

4. Графически решаем уравнение (5.5), как показано на рисунке, и находим искомое значение расхода Q.

Тип 3.Заданы: Q, L, 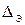, ζ_i , 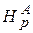, , 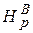ρ, 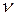. Найти d.

По своей неопределенности задача похожа на предыдущую - при неизвестном расходе нет возможности вычислить V и Re; поэтому нельзя определить ни 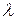, ни k. Задача может быть также решена двумя методами -

численным либо графоаналитическим.

При решении численным методом следует несколько видоизменить компактную форму уравнения Бернулли, не выражая в нем V через Q .

Оно примет вид:

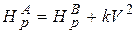, (5.7)

где

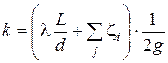. (5.8)

Последовательность операций при этом следующая:

1. Задаемся величиной допускаемой относительной ошибки вычисления диаметра Е, например, 0,001 (0,1%).

2.Задаемся любым значением диаметра .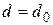

3.Вычисляем среднюю скорость в трубе .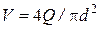

4.Вычисляем число 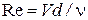и определяем режим течения.

5.Выбираем формулу для 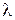и вычисляем .

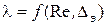6.Вычисляем коэффициент k по формуле (5.8).

7. Из формулы (5.7) определяем .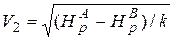

8. Находим диаметр трубопровода .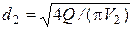

9. Если абсолютная величина 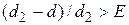, то 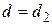; идти к пункту 3.

Иначе 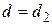(решение задачи).

При решении графоаналитическим методом применяется прежняя компактная форма уравнения Бернулли (5.5).

Последовательность операций при этом следующая:

1. Составляем таблицу, где задаемся рядом значений диаметра d в порядке возрастания.

2. Для каждого значения диаметра вычисляем 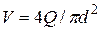, , 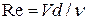определяем режим , выбираем формулу для 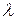и вычисляем 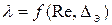, k по формуле (5.6), гидравлические потери по формуле .

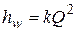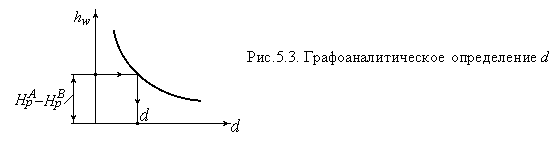
3. По полученным значениям h_w строим график 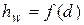(рис. 5.3).

4. Графически решаем уравнение (5.5), как показано на рисунке, и находим искомое значение диаметра d.