Путевые потери при турбулентном режиме
В отличие от ламинарного режима, зависимости для определения
гидравлических потерь, в том числе путевых, базируются исключительно на экспериментальных данных. Опыты показывают, что путевые потери при турбулентном режиме могут зависеть в общем случае от числа Рейнольдса и шероховатости трубы.
Шероховатость характеризуется двумя параметрами: абсолютной шероховатостью 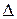 (средней высотой бугорков на внутренней поверхности трубы) и относительной шероховатостью
(средней высотой бугорков на внутренней поверхности трубы) и относительной шероховатостью 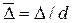 . Большую роль играет также
. Большую роль играет также
форма бугорков, их густота и характер взаимного расположения на поверхности. Эти факторы учесть и выразить какими-либо формульными зависимостями практически невозможно. Поэтому в гидравлике вводится понятие эквивалентной шероховатости 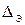 , то - есть шероховатости, приведенной к некоторому стандартному виду (с равномерно расположенными бугорками − одинаковыми зернами примерно сферической формы).
, то - есть шероховатости, приведенной к некоторому стандартному виду (с равномерно расположенными бугорками − одинаковыми зернами примерно сферической формы).
Как указывалось ранее, при турбулентном режиме у стенки имеется вязкий подслой толщиной 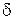 . Если толщина этого подслоя
. Если толщина этого подслоя 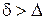 (рис.5.1, а),
(рис.5.1, а),
то выступы закрыты вязкой пленкой и в турбулентном пристенном слое жидкость, двигаясь, скользит по вязкому подслою как по жидкой смазке (по аналогии с ламинарным режимом).
Такая труба называется гидравлически гладкой.
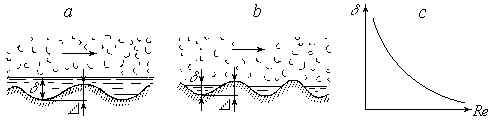
Рис.5.1. К определению гидравлически гладких и шероховатых труб
В этом случае коэффициент сопротивления трения λ не зависит от шероховатости трубы и рассчитывается по формуле Блазиуса:
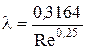 . (5.1)
. (5.1)
Если 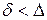 (рис. 5.1, b), труба называется гидравлически шероховатой. У такой трубы бугорки шероховатости проходят сквозь вязкий подслой и оказываются в турбулентном потоке. При этом с бугорков срываются вихри, увеличивая гидравлические потери. Коэффициент λ при этом зависит как от числа Re, так и от эквивалентной шероховатости трубы
(рис. 5.1, b), труба называется гидравлически шероховатой. У такой трубы бугорки шероховатости проходят сквозь вязкий подслой и оказываются в турбулентном потоке. При этом с бугорков срываются вихри, увеличивая гидравлические потери. Коэффициент λ при этом зависит как от числа Re, так и от эквивалентной шероховатости трубы 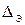 . Он может быть рассчитан по формуле Альтшуля:
. Он может быть рассчитан по формуле Альтшуля:
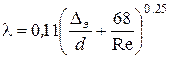 . (5.2)
. (5.2)
Толщина вязкого подслоя уменьшается с увеличением числа Re
(рис. 5.1, с). Поэтому одна и та же труба при различных числах Re может быть
либо гидравлически гладкой, либо гидравлически шероховатой.
Применение формул (5.1) либо (5.2) определяется следующим образом:
Если 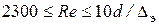 , труба считается гидравлически гладкой и применяется формула Блазиуса.
, труба считается гидравлически гладкой и применяется формула Блазиуса.
Если 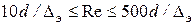 , труба − гидравлически шероховатая и
, труба − гидравлически шероховатая и
применяется формула Альтшуля.
Если 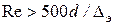 , труба называется вполне шероховатой.Этоусловие достигается при очень больших числах Re, когда в формуле Альтшуля можно пренебречь вторым слагаемым в скобках и получить формулу:
, труба называется вполне шероховатой.Этоусловие достигается при очень больших числах Re, когда в формуле Альтшуля можно пренебречь вторым слагаемым в скобках и получить формулу:
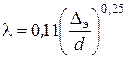 . (5.3)
. (5.3)
Эта формула называется формулой Шифринсона. Как следует из нее, в
данном случае λ не зависит от числа Рейнольдса, а зависит только от относительной шероховатости трубы. Такое течение, при котором сохраняется независимость от какого−либо критерия подобия, называется автомодельным.
При расчетах по приведенным формулам значения 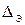 берутся из гидравлических справочников, например:
берутся из гидравлических справочников, например:
· цельнотянутые новые стальные трубы – 0,01 − 0,1;
· цельнотянутые стальные трубы, находящиеся в эксплуатации – 1,2−1,5;
· цельнотянутые стальные паропроводы перегретого пара − 1,0;
· цельносварные новые стальные трубы – 0,04 – 0,1 и т.д.
Местные потери
Для определения местных потерь необходимо знать коэффициент местного сопротивления ζ и среднюю скорость для подстановки в формулу Вейсбаха (4.43). В качестве средней скорости V обычно берется скорость в трубопроводе до местного сопротивления; если берется скорость после сопротивления, это обязательно оговаривается. Если на трубопроводе имеется несколько местных сопротивлений, потери в них суммируются. Суммирование
допускается только в случае, если расстояние между соседними местными сопротивлениями не превышает (40 – 60)d. При этом считается, что взаимное влияние местных сопротивлений отсутствует (имеются данные о том, что длина участка взаимного влияния зависит от числа Re и шероховатости трубы).
При меньшем расстоянии соседние местные сопротивления считаются одним
сопротивлением; коэффициент ζ для него определяется опытным путем.
При турбулентном режимекоэффициенты местного сопротивления ζ
не зависят от числа Рейнольдса. Их значения, например, составляют:
· вход из бака в трубу при острых кромках входа: 0,5
· выход из трубы в бак: 1
· внезапное расширение: 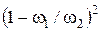
· внезапное сужение (отнесен к V2 ): 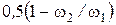
· вентиль: 2,5 – 6.
При ламинарном режиме коэффициенты местного сопротивления 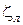 зависят от числа Рейнольдса и определяются по формуле:
зависят от числа Рейнольдса и определяются по формуле: 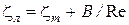 .
.
Здесь 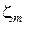 − коэффициент местного сопротивления при турбулентном режиме;
− коэффициент местного сопротивления при турбулентном режиме;
В − коэффициент, определяемый для каждого вида местного сопротивления по справочникам.
Дата добавления: 2015-10-26; просмотров: 2748;
