Случайные события. Классическое определение вероятности

Теория вероятностей изучает случайные явления, то есть такие явления, которые заранее невозможно однозначно предсказать.

Пусть выполнен некоторый комплекс условий S (говорят также проведено испытание S). Событие А, которое при S может произойти или не произойти называется случайным. Например, при бросании монеты (S) герб может выпасть или не выпасть, при выстреле стрелка (S) он может попасть в мишень, а может и не попасть в нее, при бурении разведочной скважины нефть в ней может быть или не быть обнаружена и т.д. В дальнейшем для краткости слово «случайное» мы часто будем опускать.

Событие, которое при S всегда происходит, называется достоверным ( 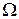); а событие, которое при S не может произойти называется невозможным(Ø). Например, при бросании игральной кости событие, состоящее в том, что выпавшее число очков будет меньше семи является достоверным, а событие, состоящее в том, что выпадает семь очков является невозможным.

События А₁, А₂, …, А_n называются несовместными,если появление одного из них исключает появление любого другого из них. Например, при бросании игральной кости можно выделить шесть несовместных событий А₁, А₂, …, А₆, соответствующих появлению определенного числа очков (от 1 до 6).

Несовместные события А₁, А₂, …, А_n называются единственно возможными (говорят также – образуют полную группу событий), если в результате S ровно одно из этих событий обязательно происходит.

События А₁, А₂, …, А_n называются равновозможными, если появление одного из них не более возможно чем появление любого другого из них. События А₁, А₂, …, А_n называются элементарными, если они единственно возможные и равновозможные.

Событие А называется благоприятствующим для В, если при наступлении А событие В всегда наступает. Любое событие благоприятствует достоверному и ни одно событие не благоприятствует невозможному событию.

Для характеристики случайности события вводится понятие вероятности – меры случайного события.

Классическое определение вероятности. Пусть имеется n элементарных событий, и пусть m событий из них благоприятствуют событию А. Вероятностью события А называется число

.

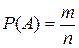Это определение не универсальное, поскольку для определения А здесь требуется выделить конечную группу элементарных событий, что не всегда возможно. Отметим следующие простейшие свойства вероятностей.

1) Вероятность любого события заключена между нулем и единицей: .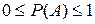

2) Вероятность достоверного события равна единице: .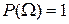

3) Вероятность невозможного события равно нулю: P(Ø)=0.

Выводы: По данной теме нами были рассмотрены виды случайных событий,классическое определение вероятности и основные свойства вероятности.

Лекции №3-4. Элементы комбинаторики. Геометрическое определение вероятности.