Формула Байеса
Пусть событие 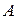 произошло, и мы хотим переоценить вероятность гипотез, которые нам были известны до опыта, то есть найти условную вероятность
произошло, и мы хотим переоценить вероятность гипотез, которые нам были известны до опыта, то есть найти условную вероятность 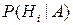 после того, как событие
после того, как событие 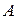 произошло.
произошло.
Теорема(Формула Байеса). Пусть 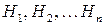 - полная группа событий и
- полная группа событий и 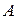 – некоторое событие положительной вероятности. Тогда условная вероятность того, что произошло событие
– некоторое событие положительной вероятности. Тогда условная вероятность того, что произошло событие 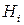 , если в результате эксперимента наблюдалось событие
, если в результате эксперимента наблюдалось событие 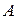 , может быть вычислена по формуле:
, может быть вычислена по формуле:
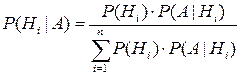 – формула Байеса.
– формула Байеса.
Пример. Есть 3 завода, производящих одну и ту же продукцию. При этом 1-й завод производит 25%, 2-й завод — 35% и 3-й завод — 40% всей производимой продукции. Брак составляет 5% от продукции 1-го завода, 3% от продукции 2-го и 4% от продукции 3-го завода. Вся продукция смешивается и поступает в продажу. Найти:
а) вероятность купить бракованное изделие;
б) вероятность того, что купленное изделие изготовлено 2-м заводом, если это изделие бракованное.
Решение. Изделие выбирается наудачу из всей произведенной продукции. Рассмотрим три гипотезы: 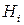 = {изделие изготовлено
= {изделие изготовлено 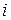 -м заводом},
-м заводом}, 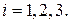 . . Вероятности этих событий даны:
. . Вероятности этих событий даны:
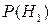 = 0,25,
= 0,25,
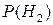 = 0,35,
= 0,35,
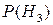 = 0,4.
= 0,4.
Пусть событие 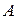 = {изделие оказалось бракованным}. Даны также условные вероятности:
= {изделие оказалось бракованным}. Даны также условные вероятности:
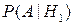 = 0,05,
= 0,05,
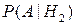 = 0,03,
= 0,03,
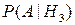 = 0,04.
= 0,04.
Тогда:
а) вероятность равна доле бракованных изделий в объеме всей продукции, то есть по формуле полной вероятности
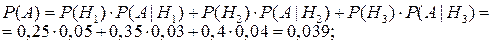
б) вероятность равна доле брака 2-го завода среди всего брака, то есть по формуле Байеса:
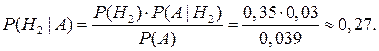
Пример. Два стрелка подбрасывают монетку и выбирают, кто из них стреляет по мишени (одной пулей). Первый стрелок попадает по мишени с вероятностью 1, второй стрелок — с вероятностью 0,001. Можно сделать два предположения об эксперименте:
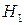 = {стреляет 1-й стрелок}
= {стреляет 1-й стрелок}
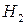 = {стреляет 2-й стрелок}.
= {стреляет 2-й стрелок}.
Априорные (a’priori —«до опыта») вероятности этих гипотез одинаковы: 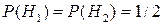 .
.
Рассмотрим событие A = {пуля попала в мишень}. Известно, что
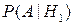 =0,5,
=0,5, 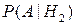 = 0,001.
= 0,001.
Поэтому вероятность пуле попасть в мишень 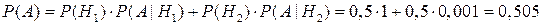 .
.
Предположим, что событие A произошло. Какова теперь апостериорная (a’posteriori — «после опыта») вероятность каждой из гипотез 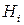 ? Очевидно, что первая из этих гипотез много вероятнее второй (а именно, в 1000 раз). Действительно,
? Очевидно, что первая из этих гипотез много вероятнее второй (а именно, в 1000 раз). Действительно,
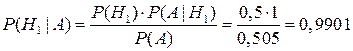 ,
,
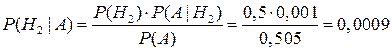 .
.
Пример. Два охотника одновременно стреляют в цель. Известно, что вероятность попадания у первого охотника равна 0,2, у второго – 0,6. В результате первого залпа оказалось одно попадание в цель. Какова вероятность того, что промахнулся первый охотник?
Решение. Событие 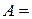 {одно попадание в цель}.
{одно попадание в цель}.
В условиях данной задачи можно сделать следующие предположения (гипотезы):
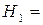 {попали в цель оба охотника},
{попали в цель оба охотника}, 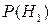 =
= 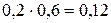 ;
;
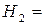 {попал в цель первый охотник, а второй промахнулся},
{попал в цель первый охотник, а второй промахнулся}, 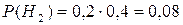 ;
;
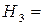 {попал в цель второй охотник, а первый промахнулся},
{попал в цель второй охотник, а первый промахнулся}, 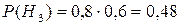 ;
;
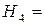 {оба охотника промахнулись},
{оба охотника промахнулись}, 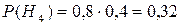 .
.
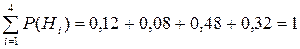
Условные вероятности события 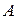 при условии осуществления каждой из гипотез:
при условии осуществления каждой из гипотез:
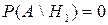 ,
,
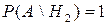 ,
,
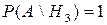 ,
,
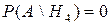 .
.
Вероятность одного попадания в цель найдем по формуле полной вероятности:
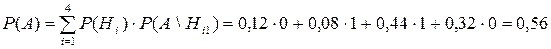 .
.
Найдем теперь вероятность того, что промахнулся первый охотник, то есть требуется переоценить вероятность 3-ей гипотезы, если известно, что произошло одно попадание:
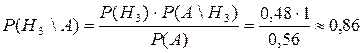 .
.
Дата добавления: 2015-10-19; просмотров: 3273;
