Формула Бернулли

Пусть проводиться серия испытаний, причем вероятность события 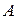в каждом испытании не зависит от исходов других испытаний. Такие испытания называют независимыми относительно события .

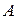Событие 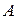в различных испытаниях может иметь либо различные вероятности, либо одну и ту же. Будем рассматривать такие испытания, в которых событие 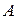имеет одну и ту же вероятность.

Схемой Бернулли называется последовательность независимых испытаний, в каждом из которых возможны лишь два исхода — «успех» (событие 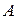произошло) и «неудача» (событие 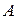не произошло), при этом «успех» в одном испытании происходит с вероятностью 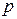, «неудача» — с вероятностью .

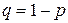Вероятность того, что событие 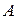произойдет ровно 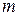раз из 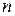испытаний, причем не важно, в какой последовательности появиться событие 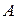, будет равна:

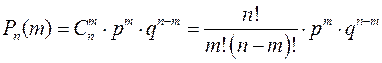– формула Бернулли.

Число успехов 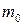, которому при заданном 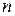соответствует максимальная биномиальная вероятность 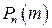, называется наиболее вероятным (наивероятнейшим) числом успехов.

В 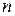испытаниях схемы Бернулли с вероятностью успеха 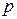наиболее вероятным числом успехов является

- единственное число 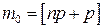, если число 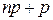не целое;

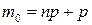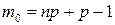- два числа и , если число 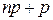целое.

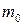удобно искать из системы неравенств: .

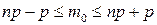Пример. Баскетболист забрасывает мяч в корзину с вероятностью 0,6. Произведено 8 бросков. Найти вероятность того, что при этом будет ровно 2 попадания. Найти наивероятнейшее число попаданий и вероятность этого числа попаданий.

Решение.Проводится серия из восьми испытаний с двумя исходами в каждом: попадание («успех») и промах («неудача»). Вероятность «успеха» при каждом испытании одна и та же: 0,6. Будем считать испытания независимыми. Требуется найти вероятность события 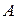={в серии из 8 испытаний «успех» произошёл 2 раза}. Имеем: , , .

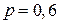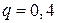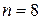По формуле Бернулли: .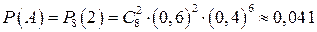

Найдём наивероятнейшее число попаданий и соответствующую вероятность. Составляем систему неравенств:

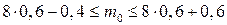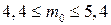, , тогда .

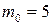Соответствующая вероятность: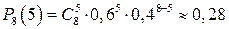

Итак, вероятнее всего из 8 бросков баскетболист попадёт 5 раз, причём вероятность этого события равна 0,28.