Локальная теорема Лапласа. Пусть теперь число испытаний велико, , и вероятность появления успеха в одном испытании достаточно велика
Пусть теперь число испытаний велико, 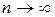 , и вероятность появления успеха в одном испытании достаточно велика. К данной схеме теорема Пуассона неприменима, а по формуле Бернулли вычисления затруднительны. Тогда справедлива теорема Лапласа.
, и вероятность появления успеха в одном испытании достаточно велика. К данной схеме теорема Пуассона неприменима, а по формуле Бернулли вычисления затруднительны. Тогда справедлива теорема Лапласа.
Локальная теорема Лапласа. Если вероятность 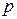 появления события
появления события 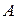 в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие
в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие 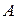 появиться ровно
появиться ровно 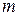 раз в
раз в 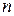 испытаниях, приближенно равна:
испытаниях, приближенно равна:
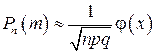 , где
, где 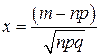 .
.
Формула 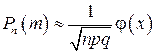 называется асимптотической формулой Лапласа.
называется асимптотической формулой Лапласа.
Функция 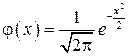 – функция Гаусса.
– функция Гаусса.
Функция Гаусса табулирована, то есть ее значения помещены в таблицы, соответствующие положительным значениям аргумента (приложение 1). Пользуясь таблицей, следует учитывать, что:
а) функция Гаусса четная, то есть 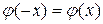 ;
;
б) при 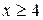 можно считать, что
можно считать, что 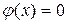 .
.
Замечание 1. Асимптотическая формула Лапласа даёт при одном и том же 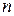 результаты тем лучше, чем ближе вероятность
результаты тем лучше, чем ближе вероятность 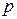 к 0,5.
к 0,5.
Замечание 2. Критерий, позволяющий однозначно определить закон:
– если 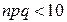 , то справедлива теорема Пуассона
, то справедлива теорема Пуассона 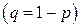 ;
;
– если 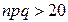 , то справедлива локальная теорема Лапласа.
, то справедлива локальная теорема Лапласа.
Пример. Вероятность попадания в мишень при одном выстреле для данного стрелка равна 0,7. Найти вероятность того, что при 200 выстрелах мишень будет поражена 160 раз.
Решение. Здесь 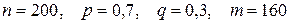 .
.
Применим локальную формулу Муавра–Лапласа.
Имеем: 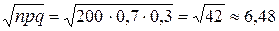 , следовательно,
, следовательно,
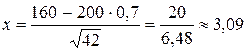 .
.
Учитывая, что: 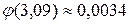 (определяем по таблице приложения 1), получим:
(определяем по таблице приложения 1), получим:
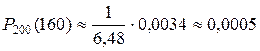 .
.
Дата добавления: 2015-10-19; просмотров: 884;
