Наращенные суммы и современные стоимости других видов постоянных рент
Ренты пренумерандо и ренты с выплатами в середине периодов.
Напомним, что под рентой пренумерандо понимается рента с платежами в начале периодов. Легко понять, что каждый член такой ренты "работает" на один период больше, чем в ренте постнумерандо. Отсюда наращенная сумма ренты пренумерандо, больше в
(1 + i) раз аналогичной ренты постнумерандо:
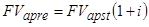
Аналогичным путем получим для годовой ренты с начислением процентов т раз в году
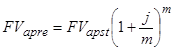
Для р-срочных рент, у которых т = 1 и т ≠ р, получим:
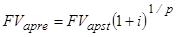
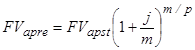
Точно такая же зависимость наблюдается и между современными стоимостями и коэффициентами приведения рент постнумерандо и пренумерандо:
Важной для практики является рента с платежами в середине периодов. Наращенные суммы и современные стоимости таких рент находим умножением соответствующих обобщающих характеристик рент постнумерандо на множитель наращения за половину периода. Так, для современных стоимостей находим следующие соотношения:
PV1/2 = PVa pst (1 + i) при р = 1, т = 1,
PV1/2 = PVa pst (1 + i) 2р при р > 1, т = 1,
PV1/2 = PVa pst (1 + j/m) m/2 при р = 1, т > 1,
PV1/2 = PVa pst (1 + j/m) m/2p при р > 1, т > 1.
Отложенные ренты.
Начало выплат у отложенной (отсроченной) ренты сдвинуто вперед относительно некоторого момента времени. Например, погашение задолженности планируется начать спустя обусловленный срок (льготный период). Очевидно, но сдвиг во времени никак не отражается на величине наращенной суммы. Иное дело современная стоимость ренты.
t PV = PVn t = Ran,in t
t PV — современная стоимость отложенной на tлет ренты.
Современная стоимость отложенной ренты используется при решении целого ряда задач, чаще всего в расчетах, связанных с выплатами различного рода накоплений.
Вечная рента.
Напомним, что под вечной рентой понимается ряд платежей, количество которых не ограничено — теоретически она выплачивается в течение бесконечного числа лет
При п ® ∞ пределом для коэффициента приведения является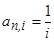 
. Откуда для вечной ренты находим:
PVa pst=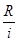 
Рента с периодом платежей, превышающим год.
Пусть r— временной интервал между двумя членами ренты, проценты начисляются раз в году. В этом случае современная стоимость первого платежа составит на начало ренты величину Tn r, второго — Tn 2r, последнего члена — Tn n, где Т — величина члена ренты, п — срок ренты, кратный r. Последовательность дисконтированных платежей представляет собой геометрическую прогрессию с первым членом Tn r, знаменателем n r, и числом членов п/r. Сумма членов такой прогрессии при условии, что Т = 1, равна:
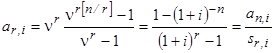
Разумеется, указанное в формуле соотношение коэффициентов приведения и наращения можно использовать в случаях, когда r — целое число лет.
Переменная процентная ставка.
Пусть для постоянной ренты постнумерандо со сроком п лет предусматривается два уровня процентной ставки, применяемые по срокам п1 и п2. В этом случае:
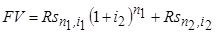
Дата добавления: 2015-10-19; просмотров: 980;