Наращенная сумма аннуитета постнумерандо
Годовая рента.
Пусть в течение п лет в банк в конце каждого года вносится по R рублей. На взносы начисляются сложные проценты по ставке i % годовых. Таким образом, имеется рента, член которой равен R , а срок — n. Все члены ренты, кроме последнего, приносят проценты — на первый член проценты начисляются п - 1 год, на второй п - 2 и т.д. На последний взнос проценты не начисляются (напомним, что рента постнумерандо). Наращенная к концу срока каждого взноса сумма составит:
Искомая величина очевидно равна сумме членов этой прогрессии.
R(1+i)n-1, R(1+i)n-2, …, R(1+i), R
Откуда

Данный коэффициент представляет собой наращенную сумму ренты, член которой равен 1:

Таким образом.
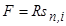
Как видим, коэффициент наращения ренты зависит только от срока (числа членов ренты) и процентной ставки. С увеличением значения каждого из этих параметров его величина растет. При i = 0 имеем S = Rn. Значения коэффициента легко табулировать.
Годовая рента, начисление процентов т раз в году.
Пусть как и выше, анализируется годовая рента постнумерандо. Однако проценты теперь начисляются т раз в году. Число членов ренты равно пт. Члены ренты с начисленными к концу срока процентами образуют ряд (перепишем его в обратном порядке):
R, R(1+  )m, R(1+
)m, R(1+  )2m, …, R(1+
)2m, …, R(1+  )(n-1)m
)(n-1)m
Нетрудно убедиться, что и в этом случае мы имеем дело с возрастающей геометрической прогрессией. Первый член прогрессии равен R, знаменатель — (1 + j/m)m. Сумма членов этой прогрессии составляет

Рента p-срочная (т = 1).
Пусть рента выплачивается р раз в году равными суммами, процент начисляется раз в конце года. Если годовая сумма платежей равна R, то каждый раз выплачивается R/p. Общее число членов ренты равно пр. Последовательность членов ренты с начисленными процентами представляет собой геометрическую прогрессию. Первый член ее равен R/p , знаменатель — (1+i)1/p Сумма членов этой прогрессии
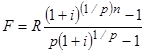
Рента p-срочная (р = т).
На практике наиболее часто встречаются случаи, когда число выплат в году равно числу начислений процентов: р = т. Для получения необходимой формулы воспользуемся замененной i на j/m , а вместо числа лет берется число периодов выплат ренты пр, член ренты равен R/p. Поскольку р = т, то в итоге получим:
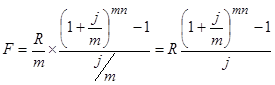
Рента p-срочная (р = т).
Общее количество членов ренты равно пр, величина члена ренты R/p. Члены ренты с начисленными процентами образуют ряд, соответствующий геометрической прогрессии с первым членом R/p и знаменателем (1 + + j/m)m/p. Сумма членов такой прогрессии составит:
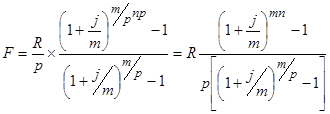
Непрерывное начисление процентов.
Обсуждение методов определения наращенных сумм дискретных рент будет неполным, если не охватить ренты с непрерывным начислением процентов. Перепишем в обратном порядке ряд платежей с начисленными непрерывными процентами. Пусть это будут ежегодные платежи постнумерандо. Получим: R, Red, Re2d, ..., Rеd. Сумма членов прогрессии равна:
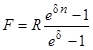
где е — основание натуральных логарифмов. Аналогично для p-срочной ренты находим:
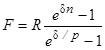
Сравнение результатов наращения годовых и p-срочных рент постнумерандо с разными условиями выплат и наращения процентов.
Обозначим сравниваемые суммы как FV (p;m) так, FV (1;1) означает наращенную сумму годовой ренты с ежегодным начислением процентов, FV (p;m) — аналогичную характеристику для ренты с начислением процентов т раз в году, наконец, S (p;∞) — наращенную сумму p-срочной ренты с непрерывным начислением процентов.
Для одних и тех же сумм годовых выплат, продолжительности рент и размеров процентных ставок (i =j = d) получим следующие соотношения:
FV (1;1) < FV (1; m) < FV (p;1) < FV (p;m) < FV (p;m) < FV (p;m) < FV (p;∞)
m >1 p > m >1 p = m>1 m > p >1
- Годовая рента, начисление процентов m раз в год

- рента р-срочная (m = 1)
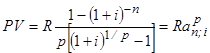
- рента р-срочная (m = p)
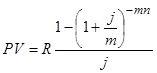
- рента р-срочная (m ≠ p)
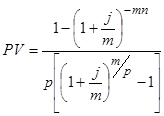
- непрерывное начисление процентов
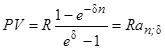
- непрерывная р-срочная рента
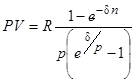
Сравнение современных стоимостей аннуитетов постнумерандо с разными условиями.
PV (1;∞) > PV (1; m) > PV (1;1) > PV (p;∞) > PV (p;m) > PV (p;m) > PV (p;m) > PV (p;1)
m > p >1 p = m>1 p > m >1
Дата добавления: 2015-10-19; просмотров: 922;
