Вычисление основных параметров аннуитета
Определение размера члена ренты
При определении размера единичного платежа ренты возможны два общих случая решения этой задачи. Они выясняются при анализе исходных данных через отнесение одно из заданных величин либо к категории наращенных сумм, либо к категории приведенных стоимостей.
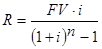
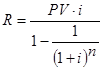
Расчет срока ренты.
Данная задача интерпретируется как задача определения срока окупаемости инвестиций и поэтому имеет широкое практическое применение.
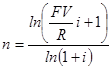
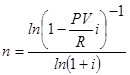
Определение размера процентной ставки.
Из формул приведенной стоимости ренты и будущей стоимости выразим множители наращения и дисконтирования ренты:
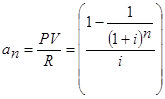
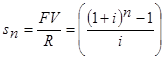
Однако прямого алгебраического решения этих уравнений относительно параметра i нет. В настоящее время по остальным характеристикам финансовой ренты рассчитывают с помощью интерполяционных формул, на основе итерационного метода Ньютона-Рафсона, или на основе разложения бинома Ньютона использовании двух-трех первых членов этого разложения.
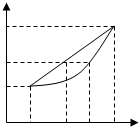
Метод линейной интерполяции

aверх , aнижн – табличное значение коэффициента наращения или приведения рент для верхнего и нижнего уровня ставок (iнижн и iверх).
а – значение коэффициента наращения или приведения, для которого определяется размер ставки.
i – интерполяционная оценка;
i’’ – точное значение.

 | |||
 |
Ньютона-Рафсона
Сущность данного метода заключается в использовании итеративного пути решения задачи, т.е. метода последовательного приближения, с применением рекуррентной формулы.
Аналитиком задается некое функциональное соотношение между параметрами ренты R, n, FV, PV и переменной x: f(x) = 0. данная переменная должна содержать искомую величину процентной ставки или вообще совпадать с ней.
Возьмем в качестве модели функции f(x) функцию вида:
sфакт – sрасч = 0
Допустим, известны исходные значения обобщающей характеристики S, разового платежа R и срока n. Тогда формула, задающая функцию для постоянной простой ренты постнумерандо, будет записана в виде:

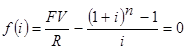
Обозначим

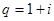
тогда
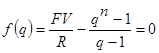
Метод Ньютона-Рафсона основан на применении рекуррентной формулы (соотношение, в котором неизвестная величина, имеющая номер, выражается через аналогичные величины с меньшими номерами) следующего вида:
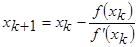
где f’(хk) – численное значение производной функции f(x) при х = хk;
k – номер итерации.
Исходное значение х0 находится с помощью таблиц коэффициентов приведения/наращения финансовых рент или методом проб и ошибок.
Тогда функция f(x) и ее производная будут выглядеть так:
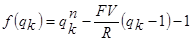
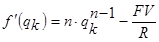
где qk – значение параметра q на k-ой итерации.
Начальное значение q0 = 1+ i0 выбирают так, чтобы значение соответствующего коэффициента sn,i было наиболее близко к заданному отношению FV/R.
При заданном отношении PV/R исходная функция записывается как:
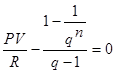
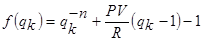
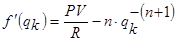
Начальное значение q0 = 1+ i0 выбирают так, чтобы значение соответствующего коэффициента аn,i было наиболее близко к заданному отношению PV/R.
Для определения точности оценки процентной ставки необходимо рассчитать для проверки коэффициенты наращения и приведения и сравнить с заданными величинами.
Дата добавления: 2015-10-19; просмотров: 765;
