Розбиття простору площиною на два півпростори

Теорема 1.4. Площина розбиває простір на два півпростори. Якщо точки X і Y належать одному півпростору, то відрізок XY не перетинає площину. Якщо ж точки X і Y належать різним півпросторам, то відрізок XY перетинає площину.

Доведення (не для запам'ятовування). Нехай α — дана площина. Позначимо точку А, що не лежить на площині α. Така точка існує за аксіомою С₁. Розіб'ємо всі точки простору, що не лежать на площині α, на два півпростори таким чином. Точку X віднесемо до першого півпростору, якщо відрізок АХ не перетинає площину α і до другого півпростору — якщо відрізок АХ перетинає площину α. Покажемо, що це розбиття простору має властивості, названі у теоремі.

Нехай точки X і В належать першому півпростору. Проведемо через точки А, X і В площину α'. Якщо площина α' не перетинає площину α, то відрізок XY також не перетинає цю площину. Допустимо, площина α' перетинає площину α (рис. 8). Оскільки площини різні, то їх перетин відбувається по деякій прямій а. Пряма а розбиває площину α' на дві півплощини. Точки X і В належать одній півплощині, а саме тій, у якій лежить точка А. Тому відрізок XY не перетинає пряму а, а отже, і площину α.

Якщо точки X і В належать другому півпростору, то площина α' свідомо перетинає площину α, тому що відрізок АХ перетинає площину α. Точки X і В належать одній півплощині розбиття площини α' прямою а. Звідси відрізок XY не перетинає пряму а, а отже, і площину α.

Якщо ж точка X належить одному півпростору, а точка В — іншому, то площина α' перетинає площину α, а точки X і В лежать у різних півплощинах площини α' відносно прямої а. Тому відрізок XY перетинає пряму а, а отже, і площину α. Теорема доведена.

 

 

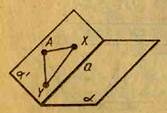Мал. 8

 

Контрольні запитання

 

1. Що таке стереометрія?

2. Сформулюйте аксіоми групи С.

3. Доведіть, що через пряму і точку, що не лежить на ній, можна провести площину, і до того ж тільки одну.

4. Доведіть, що коли дві точки прямої належать площині, то вся пряма належить цій площині.

5. Доведіть, що через три точки, що не лежать на одній прямій можна провести площину, і до того ж тільки одну.

 

Задачі

1. Точки А, В,С, D не лежать в одній площині. Доведіть, що прямі АВ і CD не перетинаються.

2. Чи можна через точку перетину двох даних прямих провести третю пряму, що не лежить з ними в одній площині? Відповідь поясніть.

3. Точки А, В, С лежать у кожній із двох різних площин. Доведіть, що ці точки лежать на одній прямій.

4. Дано три різні попарно пересічні площини. Доведіть, що якщо дві з прямих перетину цих площин перетинаються, то третя пряма проходить через
точку їх перетинання (мал. 9).

5. Дано дві площини, що перетинаються по прямій а, і пряма b, що лежить в одній із цих площин і перетинає іншу. Доведіть, що прямі а й b перетинаються.

6. Чотири точки не лежать в одній площині. Чи можуть будь-які три з них лежати на одній прямій? Відповідь поясніть.

7. Доведіть, що через пряму можна провести дві різні площини.

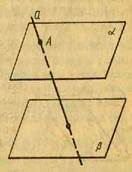
8. Дано дві площини, які не перетинаються. Доведіть, що пряма, що перетинає одну із цих площин, перетинає й іншу (мал. 10).

9. Дано дві різні прямі, що перетинаються в точці А. Доведіть, що всі прямі, які перетинають обидві дані прямі і не проходять через точку А, лежать в одній площині.

10. Доведіть, що всі прямі, які перетинають дану пряму і проходять через дану точку поза прямою, лежать в одній площині.

11. Доведіть, що коли прямі АВ і CD не лежать в одній площині, то прямі АС і BD також не лежать в одній площині.

12. Дано чотири точки, що не лежать в одній площині. Скільки можна провести різних площин, які проходять через три з цих точок? Відповідь поясніть.

13. Чи можна провести площину через три точки, якщо вони лежать на одній прямій? Відповідь поясніть.

14. Дано чотири точки. Відомо, що пряма, яка проходить через будь-які дві з цих точок, не перетинається з прямою, яка проходить через інші дві точки. Доведіть, що дані чотири точки не лежать в одній площині.

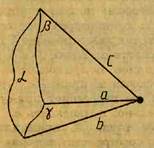Мал. 9 Мал. 10