Будь-яка система векторів, що складається з більшої кількості векторів, ніж розмірність простору Vn, буде лінійно залежною.
Означення 6. Лінійно незалежна система n-вимірних векторів 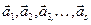 називається максимальною, або повною, лінійно незалежною системою, якщо в результаті додавання до неї будь-якого відмінного від
називається максимальною, або повною, лінійно незалежною системою, якщо в результаті додавання до неї будь-якого відмінного від 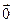 n-вимірного вектора
n-вимірного вектора 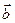 вона стає лінійно залежною.
вона стає лінійно залежною.
З розглянутого твердження випливає, що в n-вимірному просторі кожна лінійно незалежна система, яка складається з n векторів, буде максимальною, а також будь-яка максимальна, лінійно незалежна система векторів у цьому просторі складається з n векторів.
Означення 7. Базисом векторного простору Vn називається будь-яка максимальна (повна) лінійно незалежна система векторів цього простору. Так, систему векторів:
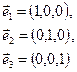
можна розглядати як базис простору V3.
Розглянемо дві системи векторів:
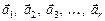 , (1.2)
, (1.2)
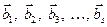 . (1.3)
. (1.3)
Система векторів (1.3) лінійно виражається через систему векторів (1.2), якщо кожний із них є лінійною комбінацією системи (1.2), тобто 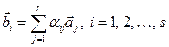 .
.
Означення 8. Дві системи векторів називаються еквівалентними, якщо кожна з них виражається лінійно через іншу.
Означення 9. Кількість векторів, що входять до будь-якої максимальної лінійно незалежної підсистеми даної системи векторів, називається рангом цієї системи.
Ранг системи векторів має відповідний зв’язок з рангом матриці. Якщо, наприклад, із компонентів векторів системи (1.2) утворити матрицю 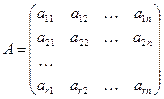 , то її ранг дорівнюватиме рангу системи векторів і вказуватиме на максимальну кількість лінійно незалежних векторів-рядків (стовпців) цієї матриці. Отже, з рангом можна пов’язати і максимальну кількість лінійно незалежних рівнянь у системі лінійних рівнянь.
, то її ранг дорівнюватиме рангу системи векторів і вказуватиме на максимальну кількість лінійно незалежних векторів-рядків (стовпців) цієї матриці. Отже, з рангом можна пов’язати і максимальну кількість лінійно незалежних рівнянь у системі лінійних рівнянь.
2. Зв’язок між базисами
Простір Vn має базис:
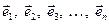 . (1.4)
. (1.4)
Якщо взяти довільний вектор 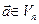 , то з максимальності лінійно незалежної системи векторів (1.4) випливає, що
, то з максимальності лінійно незалежної системи векторів (1.4) випливає, що
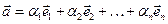 , (1.5)
, (1.5)
де хоча б одне з aі відмінне від нуля.
Отже, вектор 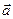 є лінійною комбінацією векторів базису. Можна показати, що вираз (1.5) — єдиний для вектора
є лінійною комбінацією векторів базису. Можна показати, що вираз (1.5) — єдиний для вектора 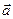 .
.
Нехай у просторі Vn задано два базиси:
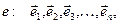 (1.6)
(1.6)
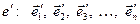 . (1.7)
. (1.7)
Кожен вектор нового базису (1.7) однозначно можна аналогічно (1.5) подати через базис (1.6) у вигляді
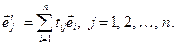 (1.8)
(1.8)
Означення 9. Матрицю 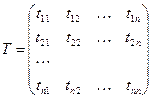 , стовпцями якої є координати векторів нового базису (1.7) у старому базисі (1.6), називатимемо матрицею переходу від базису е до базису
, стовпцями якої є координати векторів нового базису (1.7) у старому базисі (1.6), називатимемо матрицею переходу від базису е до базису 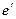 .
.
Якщо розглянути дві матриці е і 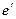 , стовпцями яких є компоненти векторів відповідно старого е і нового
, стовпцями яких є компоненти векторів відповідно старого е і нового 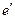 базисів, то рівність (1.8) можна записати в матричному вигляді:
базисів, то рівність (1.8) можна записати в матричному вигляді:
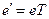 . (1.9)
. (1.9)
Водночас, якщо 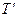 — матриця переходу від базису (1.6) до базису (1.9), маємо рівність:
— матриця переходу від базису (1.6) до базису (1.9), маємо рівність:
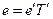 . (1.10)
. (1.10)
Скориставшись (1.9) і (1.10), запишемо:
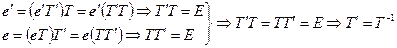 .
.
З останньої рівності випливає, що матриця переходу від одного базису до іншого завжди є невиродженою матрицею, а кількість базисів у Vn дорівнює кількості невироджених квадратних матриць. Якщо є два базиси, то матриці переходу від одного до іншого взаємно обернені.
Нехай в Vn задано два базиси (1.6) і (1.7) з матрицею переходу 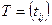 . Зв’язок між координатами довільного вектора
. Зв’язок між координатами довільного вектора 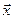 у цих двох базисах подається формулою:
у цих двох базисах подається формулою:
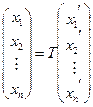 . (1.11)
. (1.11)
Помноживши рівність (1.11) зліва на матрицю 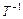 , дістанемо:
, дістанемо:
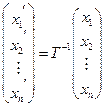 , (1.12)
, (1.12)
звідки можна визначити координати вектора в новому базисі 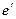 .
.
Дата добавления: 2015-10-05; просмотров: 2375;
